buuctf刷题 RSA

今天刷rsa

文章目录

RSA基础知识

python代码实现

一、RSA

二、rsarsa

三、RSA1

 四、RSA2

 五、RSA3

参考

---

RSA基础知识

#找出两个质数p，q
#n=p*q
#L=(p-1)(q-1)
#公钥e 1

python代码实现

主要是这两个算法        

                                     
需要调用函数，

import gmpy2
from Crypto.Util.number import long_to_bytes

d=gmpy2.invert(e,L) #求一个数模x的逆元y 如3*4 = 1 mod 11 -> a = gmpy2.invert(3,11)
x=gmpy2.powmod(x,d,n) 	# 求y^d mod n

其中gmpy2中的函数

	a. 模幂运算：gmpy2.powmod(a,n,p)   #对于给定的整数p,n,a,计算aⁿ mod p
	b. 对x开n次方根：gmpy2.iroot（x，n）
	c. 欧几里得算法：gmpy2.gcd（a，b）#求得a，b的最大公约数
			       gmpy2.lcm（a，b）#求得最小公倍数
	d. 扩展欧几里得：gmpy2.gcdext（e1，e2）#求式子e1*x+e2*y=gcd(e1,e2)。在RSA加密算法中利用该公式来求e的逆元d，由于实际上公钥e的选取需要保证gcd（e，ψ(n)）=1，所以在这种情况下式子的右边就是1，且通常用下面这个公式来求逆元。
	e. 模逆运算：gmpy2.invert（a，c）#对a，求b，使得a*b=1（mod c）
	f. 检测
		i. 素数检测：gmpy2.is_prime（）
		ii. 奇数检测：gmpy2.is_even（）
		iii. 偶数检测：gmpy2.is_odd（）

 另外，crypto库要在site-packages把他文件夹名字给改成大写，还要下一个pycryptodome才能用

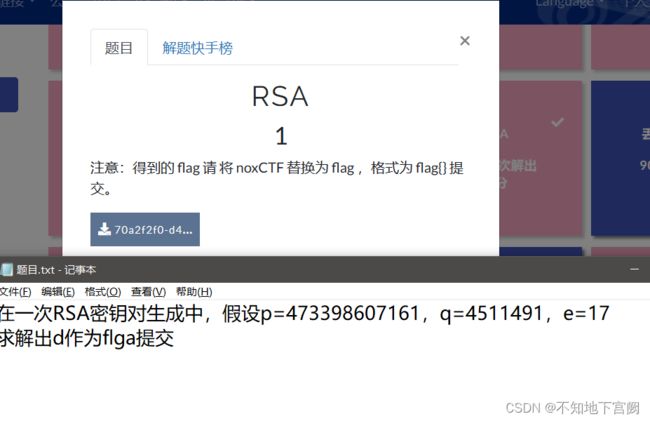
一、RSA

要求d 用到公式 

已知两个质数p、q可以得到L=(q-1)(p-1)

代码如下

import gmpy2
from Crypto.Util.number import long_to_bytes
	
if __name__ == '__main__':
    p=473398607161
	q=4511491
	e=17
	L=(q-1)*(p-1)
	d=gmpy2.invert(e,L)
	print(d)

 得到结果

125631357777427553

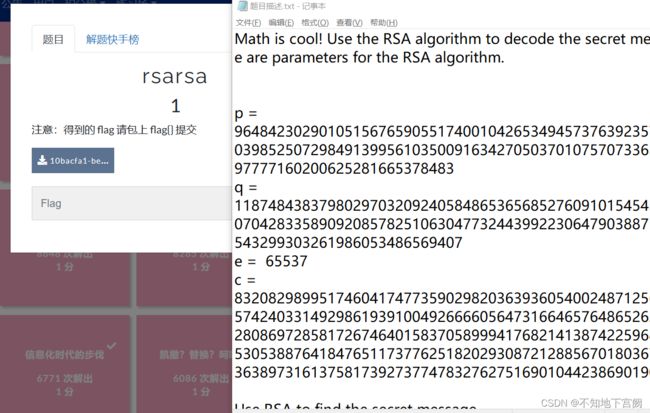
二、rsarsa

已知q、p、e、c

解密，之前也写过一样的，求出所需数据，根据公式直接解密就行

import gmpy2
from Crypto.Util.number import long_to_bytes

def Decrypt(c,e,p,q): #
	L=(p-1)*(q-1)
	d=gmpy2.invert(e,L) #求一个数模x的逆元y 如3*4 = 1 mod 11 -> a = gmpy2.invert(3,11)
	n=p*q
	m=gmpy2.powmod(c,d,n) 	# 求c^d mod n
	flag=str(m)
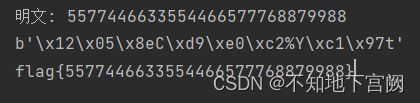
	print("明文:",flag)
	print(long_to_bytes(m))
	print("flag{"+flag+"}")
if __name__ == '__main__':
	p =  9648423029010515676590551740010426534945737639235739800643989352039852507298491399561035009163427050370107570733633350911691280297777160200625281665378483
	q =  11874843837980297032092405848653656852760910154543380907650040190704283358909208578251063047732443992230647903887510065547947313543299303261986053486569407
	e =  65537
	c =  83208298995174604174773590298203639360540024871256126892889661345742403314929861939100492666605647316646576486526217457006376842280869728581726746401583705899941768214138742259689334840735633553053887641847651173776251820293087212885670180367406807406765923638973161375817392737747832762751690104423869019034
	Decrypt(c,e,p,q)

得到结果

 flag{5577446633554466577768879988}

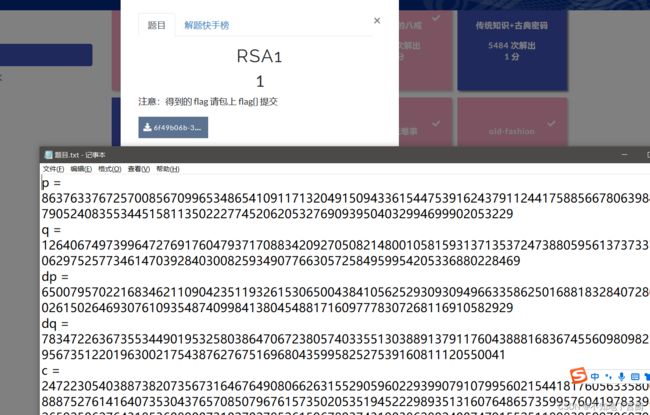
三、RSA1

 给了p、q、dp、dq、c

dq、dp是关于私钥e的参数，可以通过p、q、dp、dq得到d

再写个函数，解决

import gmpy2
from Crypto.Util.number import long_to_bytes

def Decrypt_2(c,dp,dq,p,q): #
	#L=(p-1)*(q-1)
	dd = gmpy2.gcd(p - 1, q - 1)
	d = (dp - dq) // dd * gmpy2.invert((q - 1) // dd, (p - 1) // dd) * (q - 1) + dq
	n=p*q
	m=gmpy2.powmod(c,d,n) 	# 求c^d mod n
	flag=str(m)
	print("明文:",flag)
	print(long_to_bytes(m))
	print("flag{"+flag+"}")
if __name__ == '__main__':
	p = 8637633767257008567099653486541091171320491509433615447539162437911244175885667806398411790524083553445158113502227745206205327690939504032994699902053229
	q = 12640674973996472769176047937170883420927050821480010581593137135372473880595613737337630629752577346147039284030082593490776630572584959954205336880228469
	dp = 6500795702216834621109042351193261530650043841056252930930949663358625016881832840728066026150264693076109354874099841380454881716097778307268116910582929
	dq = 783472263673553449019532580386470672380574033551303889137911760438881683674556098098256795673512201963002175438762767516968043599582527539160811120550041
	c = 24722305403887382073567316467649080662631552905960229399079107995602154418176056335800638887527614164073530437657085079676157350205351945222989351316076486573599576041978339872265925062764318536089007310270278526159678937431903862892400747915525118983959970607934142974736675784325993445942031372107342103852
	Decrypt_2(c,dp,dq,p,q)

运行得到结果

显然，flag是noxCTF{W31c0m3_70_Ch1n470wn}

提交要改成flag{}

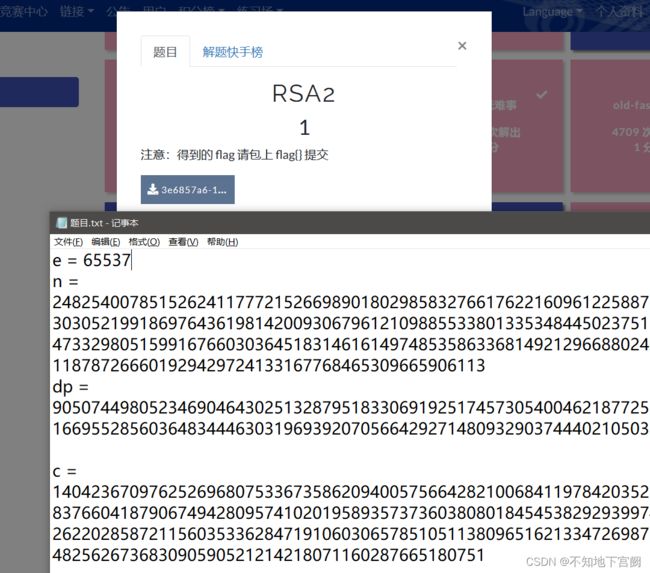
 四、RSA2

已知e，n，dp，c

def Decrypt_3(e,n,c,dp):
	for x in range(1, e):
		if(e*dp%x==1):
			p=(e*dp-1)//x+1
			if(n%p!=0):
				continue
			q=n//p
			L=(p-1)*(q-1)
			d=gmpy2.invert(e, L)
			m=gmpy2.powmod(c, d, n)
			if(len(hex(m)[2:])%2==1):
				continue
			flag = str(m)
			print("明文:", flag)
			print(long_to_bytes(m))
			print("flag{" + flag + "}")

 得到结果

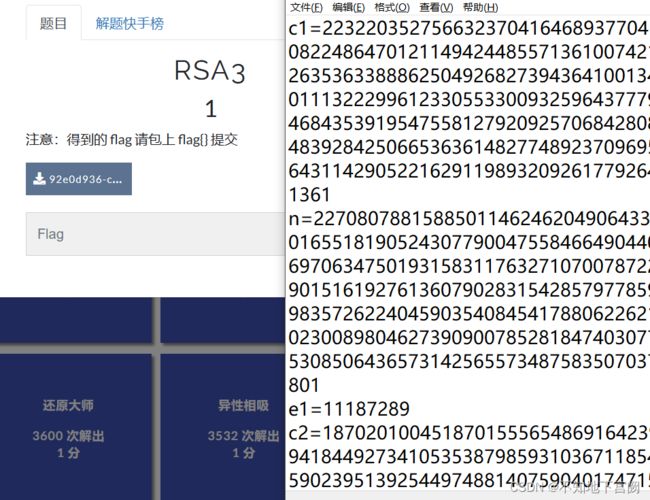
 五、RSA3

 已知c1,c2,e1,e2,n

根据公式c=m^e mod n

c1=m^e1 mod n

c2=m^e2 mod n

共模攻击

def Decrypt_4(c1,c2,e1,e2,n): # 共模攻击
	s = gmpy2.gcdext(e1, e2)
	s1,s2=s[1],s[2]
	if s1 < 0:
		s1 = - s1
		c1 = gmpy2.invert(c1, n)
	elif s2 < 0:
		s2 = - s2
		c2 = gmpy2.invert(c2, n)
	m = pow(c1, s1, n) * pow(c2, s2, n) % n # pow(c1,s1,n) -> c1**s1%n
	flag = str(m)
	print("明文:", flag)
	print(long_to_bytes(m))
	print("flag{" + flag + "}")

运行得到结果

参考

https://blog.csdn.net/serendipity1130/article/details/120154534?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522168338877516800217233679%2522%252C%2522scm%2522%253A%252220140713.130102334..%2522%257D&request_id=168338877516800217233679&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~all~top_positive~default-1-120154534-null-null.142^v86^insert_down1,239^v2^insert_chatgpt&utm_term=%E5%85%B1%E6%A8%A1%E6%94%BB%E5%87%BB&spm=1018.2226.3001.4187https://blog.csdn.net/m0_52842062/article/details/117852175