数据结构-线段树
浅谈线段树
一、什么是线段树
线段树,拆开来看就是 “线段” 和 “树”,所以顾名思义,线段树就是用来存储线段(区间)的二叉搜索树。
二、线段树的优点有哪些
既然我们要使用线段树这一数据结构进行优化,那么他一定有自己的好处:
举个例子:
一段长度为[L,R]的序列,写一个程序,需要满足进行单点修改操作和查询区间和的操作。
我们还未知线段树这一结构时,一定会想到用数组进行存储序列中的每一个元素,那么单点修改的复杂度就是O(1)的,区间查询的复杂度是O(L-R+1)的。
如果用前缀和来进行操作,那么区间查询的复杂度就是O(1)的,单点修改的复杂度是O(L-R+1)的。
可以看到两种方案都有不足之处,那么我们便引入了线段树
所以线段树它既可以满足优秀的单点修改,也可以满足优秀的区间查询,亦或是区间修改。
三、线段树的原理
线段树是将每个区间[L,R]分解成[L,M]和[M+1,R] (其中M=(L+R)/2 这里的除法是整数除法,即对结果下取整)直到 L==R 为止,实际运用中使用M=((L+R)>>1)更为快捷。
开始时是区间[1,n] ,通过递归来逐步分解,因此线段树的最大深度不超过log2n。
线段树对于每个n的分解是唯一的, 所以n相同的线段树结构相同,这也是实现可持久化线段树的基础。
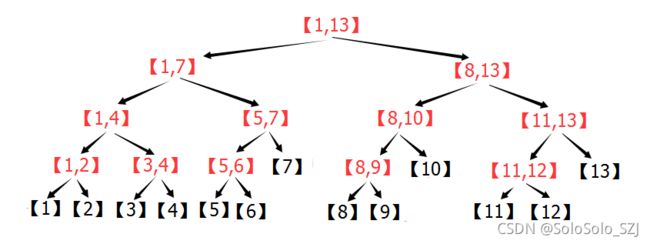 上图是一段区间[1,13]的分解过程,浅显易懂,那么分解后的部分该如何存储呢?
上图是一段区间[1,13]的分解过程,浅显易懂,那么分解后的部分该如何存储呢?
四、线段树的存储
线段树的存储通常采用堆的存储方法,即编号为id的节点的左儿子是id*2(位运算中为 (id<<1)),右儿子是id*2+1,(位运算中为 (id<<1|1)),其他的存储方式可以采用结构体存储(多用于多操作,例如 +,-,*,/)或者动态开点。
由于线段树的最大深度不超过log2n,所以对于一段长度为n的区间,如果使用堆的存储方法,则需要4n的数组来存储线段树。
五、线段树的操作
初始的一些定义
(1)偷懒的一些定义,一定要把()打好!
#define mid ((l+r)>>1) //mid简便定义
#define ls (id<<1) //左儿子简便定义left_son → ls
#define rs (id<<1|1) //右儿子简便定义right_son → rs
(2)线段树组
const int maxn = ?; //区间长度
int sum[maxn<<2]; //线段树组大小
1.初始建树
 看上图,每一个父亲节点的信息都是由子节点的信息合并而成,因此我们可以递归建树
看上图,每一个父亲节点的信息都是由子节点的信息合并而成,因此我们可以递归建树
/*初始建树*/
void Build(int id,int l,int r){
if(l==r){
sum[id] = a[l]; //如果递归到最低的点,那么该点的值 = 序列中该位置的值
return;
}
Build(ls,l,mid); //递归左儿子
Build(rs,mid+1,r); //递归右儿子
sum[id] = sum[ls]+sum[rs]; //从下到上进行信息合并
}
2.单点查询
/*单点查询*/
int Point_Query(int id,int l,int r,int goal){
if(l==r)return sum[id];
if(goal<=mid)Point_Query(ls,l,mid,goal);
else Point_Query(rs,mid+1,r,goal);
}
话说直接返回a[goal]不好吗(逃
3.单点修改 (加法
/*单点修改*/
void Point_Change(int id,int l,int r,int goal,int val){
if(l==r){
sum[id]+=val;
return;
}
if(goal<=mid)Point_Change(ls,l,mid,goal,val);
else Point_Change(rs,mid+1,r,goal,val);
sum[id] = sum[ls]+sum[rs];
}
4.区间查询
/*区间查询*/
int Segment_Query(int id,int l,int r,int goal_l,int goal_r){
int res = 0;
if(goal_l<=l&&r<=goal_r)return sum[id];
Push_Tag(id,l,r);
if(goal_l<=mid)res += Segment_Query(ls,l,mid,goal_l,goal_r);
if(goal_r>mid)res += Segment_Query(rs,mid+1,r,goal_l,goal_r);
return res;
}
5.区间修改(加法
/*区间修改*/
void Segment_Change(int id,int l,int r,int goal_l,int goal_r,int val){
if(goal_l<=l&&r<=goal_r){
Tag(id,l,r,val);
return;
}
Push_Tag(id,l,r);
if(goal_l<=mid)Segment_Change(ls,l,mid,goal_l,goal_r,val);
if(goal_r>mid)Segmemt_Change(rs,mid+1,r,goal_l,goal_r,val);
sum[id] = sum[ls]+sum[rs];
}
显然大家可以看到上面出现了Tag函数和Push_Tag函数,为什么要引入这两个函数来进行区间修改呢?
因为如果一个一个进行修改,复杂度与第一种方法相差无几,在线段树上,我们可以选择对答案有用的点进行标记,只对于有标记的代表点进行修改和查询,这样就可以大大降低复杂度了。
Tags(加法
/*处理懒标记*/
void Tag(int id,int l,int r,int val){
tag[id]+=val; //该点的懒标记加上需要加的数
sum[id]+=val*(r-l+1); //处理该[l,r]区间代表点的sum值
}
/*下放懒标记*/
void Push_Tag(int id,int l,int r){
if(!tag[id])return; //如果没有被标记就结束
Tag(ls,l,mid,tag[id]); //反之递归左儿子
Tag(rs,mid+1,r,tag[id]); //递归右儿子
tag[id]=0; //把处理完成的懒标记清空
}
六、一些题目
区间加法修改
区间加法和乘法修改
区间最值修改