数据结构的半夜----线段树学习笔记1
说过以后写blog要严肃点,我现在就严肃地修改一下,删冗余,精简语言
线段树,英文Segment Tree
这种树形数据结构十分容易形象地绘成图形
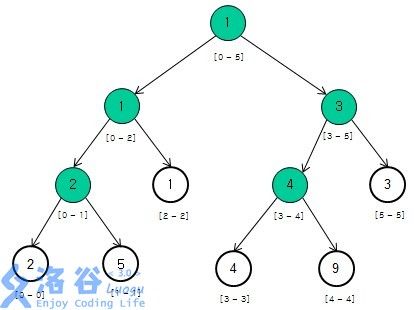
如图所示,线段树有以下性质:
- 线段树本质是棵二叉树.
- 线段树每个节点是代表一个区间[l,r],而每个节点的两个子树分别[l,mid],[mid+1,r]。
- 叶子节点l等于r且长度为1
- 线段树深度不超过logn
综上所述,我们可以按二叉树的建树方法,若节点编号为th,令节点的左儿子编号为th x 2,而右儿子记为th x 2+1。
kuanbin带你飞的前三道例题,是非常好的线段树入门例题,可以借此来初步理解线段树以及线段树的基本应用
A-敌兵布阵 HDU-1166
C国的死对头A国这段时间正在进行军事演习,所以C国间谍头子Derek和他手下Tidy又开始忙乎了。A国在海岸线沿直线布置了N个工兵营地,Derek和Tidy的任务就是要监视这些工兵营地的活动情况。由于采取了某种先进的监测手段,所以每个工兵营地的人数C国都掌握的一清二楚,每个工兵营地的人数都有可能发生变动,可能增加或减少若干人手,但这些都逃不过C国的监视。
中央情报局要研究敌人究竟演习什么战术,所以Tidy要随时向Derek汇报某一段连续的工兵营地一共有多少人,例如Derek问:“Tidy,马上汇报第3个营地到第10个营地共有多少人!”Tidy就要马上开始计算这一段的总人数并汇报。但敌兵营地的人数经常变动,而Derek每次询问的段都不一样,所以Tidy不得不每次都一个一个营地的去数,很快就精疲力尽了,Derek对Tidy的计算速度越来越不满:"你个死肥仔,算得这么慢,我炒你鱿鱼!”Tidy想:“你自己来算算看,这可真是一项累人的工作!我恨不得你炒我鱿鱼呢!”无奈之下,Tidy只好打电话向计算机专家Windbreaker求救,Windbreaker说:“死肥仔,叫你平时做多点acm题和看多点算法书,现在尝到苦果了吧!”Tidy说:"我知错了。。。"但Windbreaker已经挂掉电话了。Tidy很苦恼,这么算他真的会崩溃的,聪明的读者,你能写个程序帮他完成这项工作吗?不过如果你的程序效率不够高的话,Tidy还是会受到Derek的责骂的.
Input
第一行一个整数T,表示有T组数据。
每组数据第一行一个正整数N(N<=50000),表示敌人有N个工兵营地,接下来有N个正整数,第i个正整数ai代表第i个工兵营地里开始时有ai个人(1<=ai<=50)。
接下来每行有一条命令,命令有4种形式:
(1) Add i j,i和j为正整数,表示第i个营地增加j个人(j不超过30)
(2)Sub i j ,i和j为正整数,表示第i个营地减少j个人(j不超过30);
(3)Query i j ,i和j为正整数,i<=j,表示询问第i到第j个营地的总人数;
(4)End 表示结束,这条命令在每组数据最后出现;
每组数据最多有40000条命令
Output
对第i组数据,首先输出“Case i:”和回车,
对于每个Query询问,输出一个整数并回车,表示询问的段中的总人数,这个数保持在int以内。
Sample Input
1
10
1 2 3 4 5 6 7 8 9 10
Query 1 3
Add 3 6
Query 2 7
Sub 10 2
Add 6 3
Query 3 10
End
Sample Out
Case 1:
6
33
59
由题意可知,这是一个单点修改与区间询问的问题
个人习惯
#define lson th<<1
#define rson th<<1|1由于综上线段树的性质(2),可以用这种方式来表示他们左右子节点。
分步解构
递归建树:
void pushup(int th)
{
sum[th]=sum[lson]+sum[rson];//简单的结合律
}
void build(int l,int r,int th)
{
if(l==r)//当为叶子节点时
{
tree[th]=a[l];
return;
}
int mid=(l+r)>>1;
build(l,mid,lson);//构建左节点
build(mid+1,r,rson);//构建右节点
pushup(th);//从两个子节点更新
}
单点修改,运用二分思想
void update(int l,int r/*当前区间的左右端点*/,
int pos/*所要修改的点*/,
int th/*子树的编号*/,
int k/*所要修改的值*/)
{
if(l==pos && r==pos)//当找到这个节点时修改
{
sum[th]+=k;
return;
}
int mid=(l+r)>>1;//一分为二
if(pos<=mid) update(l,mid,pos,lson,k);//当pos在右区间时,递归右子树
else update(mid+1,r,pos,rson,k);//当pos在左区间时,递归左子树
pushup(th);//动过了当然要自下而上更新啦
}时间复杂度网上大有分析,这里便不赘述
区间询问
int query(int l,int r,int x,int y,int th)
{
if(x<=l&&r<=y){
return sum[th];//当被询问区间完全包含当前区间时,直接返回
}
int res=0;
int mid=(l+r)>>1;
if(x<=mid) res+=query(l,mid,x,y,lson);
if(mid<y) res+=query(mid+1,r,x,y,rson);
return res;
}标程
#includeB-I Hate It HDU-1754
Time Limit: 9000/3000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)Total Submission(s): 107180 Accepted Submission(s): 40245
Problem Description
很多学校流行一种比较的习惯。老师们很喜欢询问,从某某到某某当中,分数最高的是多少。
这让很多学生很反感。
不管你喜不喜欢,现在需要你做的是,就是按照老师的要求,写一个程序,模拟老师的询问。当然,老师有时候需要更新某位同学的成绩。
Input
本题目包含多组测试,请处理到文件结束。
在每个测试的第一行,有两个正整数 N 和 M ( 0
第二行包含N个整数,代表这N个学生的初始成绩,其中第i个数代表ID为i的学生的成绩。
接下来有M行。每一行有一个字符 C (只取’Q’或’U’) ,和两个正整数A,B。
当C为’Q’的时候,表示这是一条询问操作,它询问ID从A到B(包括A,B)的学生当中,成绩最高的是多少。
当C为’U’的时候,表示这是一条更新操作,要求把ID为A的学生的成绩更改为B。
Output
对于每一次询问操作,在一行里面输出最高成绩。
Sample Input
5 6
1 2 3 4 5
Q 1 5
U 3 6
Q 3 4
Q 4 5
U 2 9
Q 1 5
Sample Output
5
6
5
9
HintHuge input,the C function scanf() will work better than cin
由题意可知,此题为区间最大值与单点修改,较上面A题,编码难度较为简单
这里单点修改与建树就不再赘述,因为这里只要修改pushup()函数
void pushup(int th)
{
maxx[th]=max(maxx[lson],maxx[rson]);
}简单的询问
int query(int l,int r,int x,int y,int th)
{
if(x>r || y<l) return 0; //完全没有交集的情况
if(x<=l && r<=y) return maxx[th]; //询问区间包含当前区间
int mid=(l+r) >> 1;
return max(query(l,mid,x,y,lson),query(mid+1,r,x,y,rson)); //递归询问
}由这道题,大家应该能举一反三,写出区间最小值
标程
#includeC-A Simple Problem with Integers
Time Limit: 5000MS Memory Limit: 131072K
Total Submissions: 147182 Accepted: 45731
Case Time Limit: 2000MS
Description
You have N integers, A1, A2, … , AN. You need to deal with two kinds of operations. One type of operation is to add some given number to each number in a given interval. The other is to ask for the sum of numbers in a given interval.
Input
The first line contains two numbers N and Q. 1 ≤ N,Q ≤ 100000.
The second line contains N numbers, the initial values of A1, A2, … , AN. -1000000000 ≤ Ai ≤ 1000000000.
Each of the next Q lines represents an operation.
“C a b c” means adding c to each of Aa, Aa+1, … , Ab. -10000 ≤ c ≤ 10000.
“Q a b” means querying the sum of Aa, Aa+1, … , Ab.
Output
You need to answer all Q commands in order. One answer in a line.
Sample Input
10 5
1 2 3 4 5 6 7 8 9 10
Q 4 4
Q 1 10
Q 2 4
C 3 6 3
Q 2 4
Sample Output
4
55
9
15
Hint
The sums may exceed the range of 32-bit integers.
Source
POJ Monthly--2007.11.25, Yang Yi
我为大家大致翻译一下题干,意为需维护一个长度为N的int数组A,相对应的Q组询问,有两种操作,C l r k 意为将[l,r]区间每个数加上k,Q l r,询问[l,r]的区间和。
这便是区间修改问题。
这里要使用一种标记数组,lazytag
lazytag存储在父节点上,为该区间总共需要加上的数值,所以为了维护线段树,每次向下层递归前,都要下传lazytag
我们先来看一下区间修改函数
inline void update(ll l,/*当前区间左端点*/
ll r,/*当前区间右端点*/
ll x,/*所询问区间左端点*/
ll y,/*所询问区间右端点*/
ll th,
ll k)
{
if(x<=l && r<=y)//若完全包含,便把值记录在tag上
{
add(l,r,th,k);
return;
}
pushdown(l,r,th);//递归前下传标记
ll mid=l+r >>1;
if(x<=mid) update(l,mid,x,y,lson,k);
if(y>mid) update(mid+1,r,x,y,rson,k);
pushup(th);
}add函数
inline void add(ll l,ll r,ll th,ll k)
{
tag[th]+=k;//tag更新
sum[th]+=(r-l+1)*k;//自身维护
return;
}这里有个pushdown函数,是pushup函数的反向操作
inline void pushdown(ll l,ll r,ll th)
{
if(tag[th]==0) return;//若tag为0则返回
ll mid=l+r >>1;
add(l,mid,lson,tag[th]);//下传标记
add(mid+1,r,rson,tag[th]);
tag[th]=0;//别忘了清零
}这里为什么只下传一层呢:因为正如之前所说,每次向下递归前都要下传标记,所以到下层标记自然会下传
所以这里的询问有了些小小的变化
ll query(ll l,ll r,ll x,ll y,ll th)
{
if(x<=l && r<=y)
{
return sum[th];
}
ll mid=l+r >>1;
ll res=0;
pushdown(l,r,th);
if(x<=mid) res+=query(l,mid,x,y,lson);
if(y>mid) res+=query(mid+1,r,x,y,rson);
return res;
}然而为什么要用longlong呢,题中明明说是int数组
这时我们再通读题面,会发现一行话
The sums may exceed the range of 32-bit integers.
区间和可能会超过32位int类型
这便是要用longlong的原因
标程
#include理解了之后代码难度并不是非常大,毕竟只是最最基础的应用而已。