C++面试准备汇总

1、多态、虚函数原理、纯虚函数、析构函数可以使用虚函数吗？

答：（1）分为编译时多态（编译时就确定），比如函数重载就是这种情况，通过参数类型或数量不同可以实现；
还有运行时多态（运行时才确定），使用虚函数机制，可以通过父类指针来调用派生类的函数，
（2）具体实现机制是每个对象存在一个虚函数表，调用函数时会通过这个虚函数表去查询具体需要调用哪个版本的函数；
（3）纯虚函数是指基类没有提供函数的定义需要派生类自行实现，普通虚函数时基类存在一个版本的函数
（4）对于存在派生关系的类的析构函数应该使用虚函数，因为这样通过释放基类对象指针来回收资源时可以回收派生类的对象的全部资源，避免内存泄漏；但是不存在派生关系的类一般析构函数不设置为虚函数，因为设置为虚函数需要增加额外的空间来存放虚函数表，而且调用析构函数时需要去查询相应的版本，因此空间和时间上效率都会受到影响，这也是C++默认析构函数不设置为虚函数的原因。

2、内存泄漏类型

答：从发生方式看可以分为（1）常发性内存泄漏：发生内存泄漏的代码多次被运行，每次运行导致一块内存泄漏；
（2）偶发性内存泄漏：只有在特定条件下才会发生，因此要发现这个问题测试环境和测试方法都很重要；
（3）一次性内存泄漏。发生内存泄漏的代码只会被执行一次。比如在构造函数中分配内存，但是在析构函数中没有释放该内存；
（4）隐式内存泄漏。程序在运行过程中不停地分配内存，知道结束时才释放内存，严格来说这里并没有发生内存泄漏，但是对一个服务器程序，可以需要连续运行很长时间，不及时释放内存可能导致最终耗尽系统的所有内存。

3、TCP三次握手、四次挥手

三次握手：
（1）第一次握手，建立连接时，客户端发送SYN包(syn=j)到服务器，并进入SYN_SEND状态，等待服务器确认。
（2）第二次握手，服务器收到SYN包，必须确认客户端的SYN（ack=j+1），同时自己也发送一个SYN包（syn=k），即SYN+ACK包，此时服务器进入SYN_RECV状态。
（3）第三次握手，客户端收到服务器的SYN+ACK包，向服务器发送确认包ACK(ack=k+1)，此包发送完毕，客户端和服务器进行ESTABLISHED状态，完成3次握手。
之后客户端与服务器开始传送数据。

四次挥手
（1）第一次挥手：客户端发送释放连接报文，将FIN置1，序号为u，客户端进入FIN_WAIT_1状态（终止等待1）
（2）第二次挥手：服务器收到FIN后，发送确认报文，确认号为u+1，自己本身的序号是v，此时服务器进入CLOSE_WAIT状态
（3）第三次挥手：服务器已经没有要发送给客户端的数据了，此时服务器发送释放连接报文，将FIN置1，确认号还是u+1,自己本身的序号是w，此时服务器进入LAST-ACK状态
（4）第四次挥手：客户端收到服务器发送的释放连接报文后，需要发送确认报文，将ACK置1，确认号为w+1,然后进入TIME-WAIT状态，经过2个最长报文段寿命后，进入CLOSED状态

4、C++11新特性

（1）nullptr
引入nullptr替换NULL，nullptr能隐式转换成任何指针类型，也可以进行相等或不等的判断，避免使用NULL时，编译器有时会定义为(void*)0，有时会直接定义为0，这会导致一些重载的混乱。
（2）类型推导
引入auto和decltype，可以实现类型推导，简化代码
（3）引入基于范围的for循环，更加简洁
（4）统一了初始化列表
（5）Lambda表达式，提供一个类似匿名函数的特性，在需要一个函数，但是又不想费力去命名的时候使用
（6）引入std::array
保存在栈内存中，相比于vector，可以获得更高的性能
（7）引入std::forward_list
单向链表
（8）引入两组无序容器
unordered_map/unordered_multimap和unordered_set/unordered_multiset，使用哈希表实现，插入和搜索的时间复杂度是O(常数)
(9) 引入std::tuple
(10) 提供正则表达式
（11）对线程提供语言级的支持
（12）新增右值引用和move语义
（13）改善智能指针，摒弃auto_ptr

5 STL各种容器的底层实现

（1）vector
使用数组实现，查询、尾部插入删除时间复杂度为O(1)，其他位置删除和插入时间复杂度为O(n)
（2）list
底层为双向链表，支持快速增删
（3）deque
双端队列，底层是中央控制器和多个缓冲区，类似于vector和list的结合体，头尾插入和删除的时间复杂度为O(1)
（4）stack
底层一般用list或deque实现，封闭头部即可
（5）queue
底层一般用list或deque实现，封闭头部即可
（6）set
底层为红黑树，有序，不重复
（7）multiset
底层为红黑树，有序，可重复
（8）map
底层为红黑树，有序，不重复
（9）multimap
底层为红黑树，有序，可重复
（10）unordered_set
底层是哈希表，无序，不重复
（11）unordered_map
底层是哈希表，无序，不重复
（12）priority_queue
底层是堆，可以指定小顶堆或大顶堆

6、快速排序

时间复杂度O(nlogn)，辅助空间O(logn)~O(n)，不稳定

时间复杂度：O(nlogn)，不稳定
C++实现如下：

#include 
#include 
using namespace std;

void fast_sort1(vector<int> &v, int a, int b){
    if(a >= b || a<0 || a>=v.size() || b<0 || b>=v.size()) return;
    int tmp = v[a];
    int left = a;
    int right = b;
    bool flag = false; // false表示从右到左
    while(left != right){
        if(!flag){
            if(v[right] > tmp)
                --right;
            else{
                v[left] = v[right];
                ++left;
                flag = true;
            }
            continue;
        }
        else{
            if(v[left] < tmp)
                ++left;
            else{
                v[right] = v[left];
                --right;
                flag = false;
            }
            continue;
        }
    }
    v[left] = tmp;
    fast_sort1(v,a,left-1);
    fast_sort1(v,left+1,b);
}

int main() {
    vector<int> v{1,6,2,3,5,4,4};
    fast_sort1(v,0,v.size()-1);
    for(auto mem : v)
        cout << mem << " ";
    cout << endl;
    return 0;
}

更简洁的实现见排序专项博客

7、堆排序

时间复杂度：O(nlogn) ，辅助空间O(1)，不稳定

时间复杂度:O(nlog(n))，不稳定
C++实现

#include 
#include 
using namespace std;

void swap(vector<int> &v, int a, int b){
    int tmp = v[a];
    v[a] = v[b];
    v[b] = tmp;
}
// n表示最大操作下界（操作范围不包含n），操作范围是[0-n)
// 功能：对根节点、左子树、右子树，选出值最大的结点并交换到根结点中，若有交换，对交换的结点继续进行相同的操作
void heapify(vector<int> &v, int n, int root_idx){
    if(root_idx >= n) return;
    int max_idx = root_idx;
    int left_idx = 2*root_idx + 1;
    int right_idx = 2*root_idx + 2;
    if(left_idx <= n && v[left_idx] > v[max_idx]) max_idx = left_idx;
    if(right_idx <= n && v[right_idx] > v[max_idx]) max_idx = right_idx;
    if(root_idx != max_idx){
        swap(v,root_idx,max_idx);
        heapify(v,n,max_idx);
    }
}
void build_heap(vector<int> &v){
    int parent_idx = (v.size()-2)/2; // 构建大顶堆从最后一个结点的父结点开始
    for(int i=parent_idx; i>=0; --i)
        heapify(v,v.size()-1,i);
}
void heap_sort(vector<int> &v){
    build_heap(v);
    for(int i=v.size()-1; i>=0; --i){
        swap(v,0,i); // 每次交换根节点和最后一个操作结点
        heapify(v,i-1,0); // 然后对根结点继续进行heapify
    }
}

int main() {
    vector<int> v{7,5,6,3,2,1};
    heap_sort(v);
    for(auto mem : v)
        cout << mem << " ";
    cout << endl;
    return 0;
}

更好的实现见排序专项博客

8、手写string类

参考手写string专项博客

9、手写strcpy函数

C语言库函数
注意点：注意两个指针都不能空，注意返回char *，这样可以重复调用

char *strcpy1(char *dest, const char* src){
    assert(dest != nullptr && src != nullptr);
    char *address = dest;
    while((*dest++=*src++) != '\0') ;
    return address;
}

11、手写strcat函数

这里是默认字符数组最后结束带有’\0’

char *my_strcat(char *dest, const char *src){
    char *p = dest;
    assert(dest != nullptr && src != nullptr);
    while(*dest != '\0') ++dest; //先让dest
    while((*dest++=*src++) != '\0') ;
    return p;
}

int main() {
    char dest[20] = "hello "; // 注意调用my_strcat的第一个参数要保证有足够的空间存放第二个参数的内存，因此不能是char *dest="hello "来初始化
    char *src = "world";
    printf("%s\n",dest);
    my_strcat(dest,src);
    printf("%s\n",dest);

    cout << strlen(dest) << endl;
    cout << strlen(src) << endl;
    cout << sizeof(dest) << endl;
    cout << sizeof(src) << endl;
    strcat(dest,src);
    printf("%s\n",dest);
    return 0;
}

12 在str1中用str3替换所有的str2

C语言实现

/* 功能：实现字符串的替换
 * 在str1中将str2替换成str3
 * */
void str_replace(char *str1, const char *str2, const char *str3){
    int i,j,k,done,count=0,gap=0;
    char temp[MAXSIZE];
    for(i=0; i<strlen(str1); i+=gap){
        if(str1[i] == str2[0]){
            done = 0; // 用来标记是否在str1中找到str2
            for(j=i,k=0; k<strlen(str2); ++j,++k){
                if(str1[j] != str2[k]){
                    done = 1;
                    gap = k;
                    break;
                }
            }
            if(done == 0){
                for(j=i+strlen(str2),k=0; j<strlen(str1); ++j,++k){ // 保存str1中剩余字符
                    temp[k] = str1[j];
                }
                temp[k] = '\0';
                for(j=i,k=0; k<strlen(str3); ++j,++k){ // 字符串替换
                    str1[j] = str3[k];
                    ++count;
                }
                for(k=0; k<strlen(temp); ++j,++k){ // 剩余字符串回接
                    str1[j] = temp[k];
                }
                str1[j] = '\0'; // 在字符数组str1末尾加上'\0'，使他成为字符串
                gap = strlen(str2);
            }
        }else{
            gap = 1;
        }
    }
    if(count == 0){
        printf("Can't find the replace string!\n");
    }
}

C++实现，利用了replace函数

/*
 函数说明：对字符串中所有指定的子串进行替换
 参数：
string resource_str            //源字符串
string sub_str                //被替换子串
string new_str                //替换子串
返回值: string
 */
string& subreplace(string &resource_str, const string &sub_str, const string &new_str)
{
    string::size_type pos = 0;
    while((pos = resource_str.find(sub_str)) != string::npos)   //替换所有指定子串
    {
        resource_str.replace(pos, sub_str.length(), new_str);
    }
    return resource_str;
}

13 冒泡排序

思想：沉底，每次把最小的沉到最后（方式是不断比较前后元素，若前元素大于后元素，则交换），然后不断缩小下界
时间复杂度O(n²)，辅助空间复杂度O(1)
C++实现

/*
 * 功能：实现冒泡排序
 */
void swap(vector<int> &nums, int i, int j){
    int tmp = nums[i];
    nums[i] = nums[j];
    nums[j] = tmp;
}

void bubbleSort(vector<int> &nums){
    for(int i=0; i<nums.size(); ++i){
        for(int j=0; j<nums.size()-i-1; ++j){
            if(nums[j] > nums[j+1]) swap(nums,j,j+1);
        }
    }
}

14 选择排序

思想：每次找最小，然后交换，之后不断缩小上界
时间复杂度O(n²)，辅助空间复杂度O(1)

void selectSort(vector<int> &nums){
    int min_idx;
    for(int i=0; i<nums.size()-1; ++i){
        min_idx = i;
        for(int j=i+1; j<nums.size(); ++j){
            if(nums[j] < nums[min_idx]) min_idx= j;
        }
        if(min_idx != i) swap(nums,i,min_idx);
    }
}

15 排序时间复杂度总结

16 插入排序

思想：从前往后遍历，保存当前元素值，每次由后往前找当前元素在目标范围内的正确位置，若还没找到就将元素后移，最终找到后就将保存值放入正确的位置
时间复杂度O(n²)，空间复杂度O(1)，稳定

void insertSort(vector<int> &nums){
    int j;
    for(int i=1; i<nums.size(); ++i){
        int tmp = nums[i];
        j = i-1;
        while(j>=0 && nums[j]>tmp){
            nums[j+1] = nums[j];
            --j;
        }
        nums[j+1] = tmp;
    }
}

17 希尔排序

18 系统调用

调用函数时操作系统发生了什么？
eg:
int main(){
whoami();
}

void whoami(){
printf(“I am moumoumou”);
}

不可以直接跳到或move whoami的内存位置，因为这样涉及安全问题。

**凭什么不让跳？**硬件设计实现，区分用户态，内核态，分别对应用户段，内核段，每次检测当前特权级别CRL和目标特权级别DRL

**进入内核的方法？**可以是中断

19 函数调用内步原理

1、保存当前状态
2、保存下一条指令
3、跳转到被调用函数，有返回值就返回
4、释放函数在栈中的空间
5、恢复之前的状态并开始执行下一条指令

__stdcall：是函数调用约定的一种，函数调用约定主要约束两件事：‘
1、参数传递顺序
2、调用的堆栈由谁清理（调用函数还是被调用函数）
对应__stdcall:
1、参数从右向左压入堆栈
2、函数被调用者修改堆栈
stdcall不支持可变参数，_cdecl（堆栈由调用者管理）支持可变参数

20 跨文件共享全局变量

使用extern，如果只在本文件使用就使用static

21 ping过程发生了什么？

（1）发起主机会构建ICMP报文，再加上目的IP地址交个IP协议
（2）IP协议会加上目的IP、源IP、控制信息，同时获取目的主机的MAC地址，如果当前没有目的主机的MAC地址时，会通过ARP协议去获取，在经过数据链路层加入必要的信息封装成帧，在经过物理层传输
（3）目的主机接收到后数据后，检查MAC、IP是否匹配，符合就接收，再经过IP层解析，再经过ICMP协议解析并构建一个ICMP的应答包发回去
（4）源主机受到应答包后经过判断收发时间来判断目的主机是否到达以及网络连通性如何

AB主机中间一个交换机ApingB的原理，交换机做了什么？
答：当交换机收到主机A的数据帧后，会在MAC地址表中查询是否存在目标MAC地址信息，如果有，那么就根据MAC地址表，将数据帧从对应的接口发送出去，形成单播；如果没有，那么交换机会从不是入口的其他所有接口进行广播，之后只有主机B收到并回应了，当交换机收到回应信息后，会将主机B的mac地址和对应的接口存放到MAC地址表中。

22 哈希冲突后怎么解决？

（1）开放地址法，将出现冲突的元素放在下一个空的散列地址
（2）拉链法，对出现冲突的使用链表存放
（3）再哈希法，对出现冲突的元素再哈希
（4）公共溢出区法，将出现冲突的元素存放在溢出表中，这样查找时先在哈希表中查找，如果找不到再去溢出表中顺序查找

23 gdb调试（另外学）

基本命令：
（1）编译命令与启动

g++ -g test.cpp -o test
gdb test

（2）设置参数
set args
（3）设置断点
break/b 行号
（4）运行到断点处
run/r
(5) 单步执行但不会进入函数内部
next/n
(6) 单步执行而会进入函数内部、
step/s
(7) 打印变量值
print 变量名
(8) 继续到下一个断点
c/continue
(9) 设置变量值
set var 变量名 = 变量值
（10）退出
quit/q

24 一个程序运行起来发生了什么？

25 connect函数发生了什么？（网络编程，另外学）

作用：客户端通过connect函数来建立和服务器的连接，原型如下：

int connect(int clientfd, const struct sockadd *addr, socklen_t addrlen);

其中addr是服务器的套接字地址，addrlen=sizeof(sockaddr_in)是套接字地址长度；clientfd是连接成功后可以读写的描述符

26 套接字五元组（稍后学）

27 进程间的通信（主要问共享内存的实现）

进程间可以通过（IPC）共享内存、管道、消息队列、信号、信号量、套接字来实现通信。

参考：https://www.bilibili.com/video/BV1YD4y127aM?from=search&seid=6356779829428446256

通信有以下情况：
（1）数据传输
（2）共享数据
（3）通知事件

管道：|实现，如a|b会将a进程的输出传给进程b（命令行经常用到），同一个系统中，现在用的少
消息队列：同一个系统中，消息队列可以读写，现在用的少
信号：（有专题视频），比如kill命令
共享内存：允许多个进程访问同一个内存空间
信号量：
socket：（有专题视频）

共享内存和信号量经常结合起来用
现在比较火的有消息中间件如Redis（封装了底层的函数，提供接口，方便使用）
参考https://www.freecplus.net/6cb9ad02d7d64d6eb2f8e241b1158aed.html

1、共享内存：允许多个进程访问同一个内存空间，本身没有提供锁的机制，如果要加锁可以使用信号量
（1）头文件：

#include 
#include 

（2）获取或创建共享内存
shmget函数

int shmget(key_t key, size_t size, int shmflg);

key是编号（键值），一般是16进制；size是共享内存的大小；shmflg是共享内存的访问权限。如果不存在就创建，否则就获取。
（3）把共享内存连接到当前的地址空间

void *shmat(int shm_id, const void *shm_addr, int shmflg);

shm_id是shmget的返回值，shm_addr是指把共享内存连接到当前进程的哪个地址上，通常为空，让系统来选择；shmflg是一组标志位，一般为空；返回值为指向共享内存第一个字节的指针，失败就返回-1.
（4）将共享内存从当前进程分离

int shmdt(const void *shmaddr);

其中shmaddr是shmat的返回值；是shmat的反操作，调用成功时返回0，失败时返回-1.

（5）删除共享内存

int shmctl(int shm_id, int command, struct shmid_ds *buf);

shm_id是shmget的返回值，command一般填IPC_RMID，buf一般填0

示例程序：

/*
 * 程序名：book258.cpp，此程序用于演示共享内存的用法
 * 作者：C语言技术网(www.freecplus.net) 日期：20190525
*/
#include 
#include 
#include 
#include 
#include  

int main()
{
  int shmid; // 共享内存标识符
 
  // 创建共享内存，键值为0x5005，共1024字节。
  if ( (shmid = shmget((key_t)0x5005, 1024, 0640|IPC_CREAT)) == -1)//地址使用16进制，方便查看
  { printf("shmat(0x5005) failed\n"); return -1; }
   
  char *ptext=0;   // 用于指向共享内存的指针
 
  // 将共享内存连接到当前进程的地址空间，由ptext指针指向它
  ptext = (char *)shmat(shmid, 0, 0);
 
  // 操作本程序的ptext指针，就是操作共享内存
  printf("写入前：%s\n",ptext);
  sprintf(ptext,"本程序的进程号是：%d",getpid());
  printf("写入后：%s\n",ptext);
 
  // 把共享内存从当前进程中分离
  shmdt(ptext);
   
  // 删除共享内存
  // if (shmctl(shmid, IPC_RMID, 0) == -1)
  // { printf("shmctl(0x5005) failed\n"); return -1; }
}

ipcs -m可以查看系统的共享内存
用ipcrm -m 共享内存编号，可以手工删除共享内存
oracle数据库就是使用了共享内存和信号量

2、信号量
信号量（信号灯）本质上是一个计数器，用于协调多个进程（包括但不限于父子进程）对共享数据对象的读/写。它不以传送数据为目的，主要是用来保护共享资源（共享内存、消息队列、socket连接池、数据库连接池等），保证共享资源在一个时刻只有一个进程独享。

信号量是一个特殊的变量，只允许进程对它进行等待信号和发送信号操作。最简单的信号量是取值0和1的二元信号量，这是信号量最常见的形式。锁的机制就是使用了信号量

通用信号量（可以取多个正整数值）和信号量集方面的知识比较复杂，应用场景也比较少。
（1）头文件

#include 
#include 
#include 

参考https://www.freecplus.net/91049192da9e435a92209b287a220af8.html

用信号量给共享内存加锁
其实就是信号量加锁，再使用共享内存。

3、信号
在真实的项目中，后台服务程序没有交互的界面，常驻内存中，周期性或通过事件唤醒的方法运行程序。
如何让程序在后台中运行？
方式一：执行程序命令后面加上&，这样Ctrl+C也不能使进程结束，killall加程序名可以杀死进程
方式二：使用fork()新建子进程，然后父进程退出，此时子进程由系统托管
杀死进程的方式：
1）killall 程序名
2）先用“ps -ef|grep 程序名”找到程序的进程编号，然后用“kill 进程编号”。
3）如果是非后台运行的程序，可以使用Ctrl+C
这三种方式都是使用了信号，程序捕捉到了这些信号，然后执行响应

signal信号是进程之间相互传递消息的一种方法，信号全称为软中断信号，也有人称作软中断，从它的命名可以看出，它的实质和使用很象中断。

参考：https://www.freecplus.net/eec5c39aa63b45ad946f1cc08134d9f9.html
软中断信号（signal，又简称为信号）用来通知进程发生了事件。进程之间可以通过调用kill库函数发送软中断信号。Linux内核也可能给进程发送信号，通知进程发生了某个事件（例如内存越界）。

注意，信号只是用来通知某进程发生了什么事件，无法给进程传递任何数据，进程对信号的处理方法有三种：

1）第一种方法是，忽略某个信号，对该信号不做任何处理，就象未发生过一样。

2）第二种是设置中断的处理函数，收到信号后，由该函数来处理。

3）第三种方法是，对该信号的处理采用系统的默认操作，大部分的信号的默认操作是终止进程。

常用信号：

更多的信号知识：

4、socket
见另外一个博客

28 fork的返回值

对于子进程返回0，对于父进程返回子进程的id

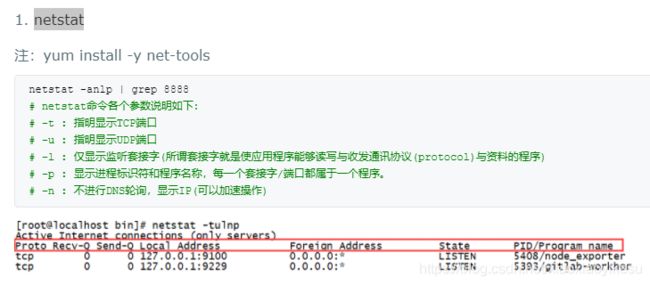
29 查看端口占用情况的linux命令

netstat

30 编程题汇总

30.1 字符串匹配

判断一个字符串中的字母是不是都包含在另一个中
思路：使用哈希集合先将主字符串字母存放起来，再遍历子串，判断每一个字符是否都在集合中即可

#include 
#include 
#include 
using namespace std;

bool judge(const string &s1, const string &s2){
    unordered_set<char> st;
    for(auto m : s1){
        st.insert(m);
    }
    for(auto m : s2){
        if(st.find(m) == st.end()) return false;
    }
    return true;
}

int main() {
    std::cout << judge("abced","abf") << std::endl;
    return 0;
}

30.2 按奇偶排序数组

给定一个非负整数数组 A，返回一个数组，在该数组中， A 的所有偶数元素之后跟着所有奇数元素。
你可以返回满足此条件的任何数组作为答案。
leetcode 905题

class Solution {
public:
    vector<int> sortArrayByParity(vector<int>& A) {
        int sz = A.size();
        if(sz < 2) return A;
        int l=0, r=sz-1, tmp;
        while(l<r){
            while(l<r && A[l]%2 == 0) ++l;
            while(l<r && A[r]%2 == 1) --r;
            if(l<r){
                tmp = A[l];
                A[l] = A[r];
                A[r] = tmp;
            }
        }
        return A;
    }
};

30.3 定义单链表的结构体以及链表的反转函数

定义链表结点结构体：值、next、构造函数
反转函数：先遍历一遍，在反转，使用哑结点可以使得代码更加简洁，最后不要忘了next要置为nullptr

#include 
#include 
using namespace std;

struct ListNode{
    int val;
    ListNode* next;
    ListNode(int v):val(v),next(nullptr){}
};

ListNode *reverseList(ListNode *head){
    vector<ListNode*> v;
    while(head){
        v.push_back(head);
        head = head->next;
    }
    ListNode *ret = new ListNode(0);
    ListNode *cur = ret;
    for(int i=v.size()-1; i>=0; --i){
        cur->next = v[i];
        cur = cur->next;
    }
    cur->next = nullptr;
    return ret->next;
}

30.4 二叉树中的最大路径和

对于每个二叉树结点来说，有三种选择：（1）左中右，不能继续往上（2）左中，可以继续往上（3）右中，可以继续往上
考虑负数：因此左右结点不一定加入，需要和0比较
因此当前结点返回值是左中和右中的最大值，而最大值需要去比较左中、右中、左中右的最大值
这道题的难点在于：分解子问题，递归子函数不是最终的答案，答案产生在当前递归过程中；要考虑负数的情况

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    int dfs(TreeNode *root, int &val){
        if(root == nullptr) return 0;
        int left_val = max(0, dfs(root->left, val));
        int right_val = max(0, dfs(root->right, val));
        int ret = root->val + max(left_val,  right_val);
        int tmp = root->val + left_val + right_val;
        val = max(val, max(ret, tmp));
        return ret;
    }
    int maxPathSum(TreeNode* root) {
        int val = INT_MIN;
        dfs(root, val);
        return val;
    }
};

30.5 从后往前是字符串匹配

本质来说还是字符串匹配，可以先让主串进行翻转，然后用kmp算法，最后的返回值需要处理一下

#include 
#include 
#include 
using namespace std;

void getNext(const string &s, vector<int> &next){
    int sz = s.size();
    int j=0,k=-1; // j是遍历子串的索引，而k是指已匹配的长度
    next[0] = -1; // 首先注意到为了处理方便next数组是右移了一位，第一个值为-1是为了处理方便
    while(j<sz){
        if(k==-1 || s[j]==s[k]) next[++j] = ++k;
        else k = next[k];
    }
}

// s1是主串，s2是子串
int kmp(const string &s1, const string &s2){
    int sz1 = s1.size(), sz2 = s2.size();
    vector<int> next(sz2);
    getNext(s2,next);
    int i=0,j=-1; // i是主串遍历索引，j是子串遍历索引，初始值为-1，是为了处理方便
    while(i<sz1 && j<sz2){
        if(j == -1 || s1[i] == s2[j]){
            ++i;
            ++j;
        } else
            j = next[j];
    }
    if(j>=sz2)  return(i-j);
    else return -1;
}
int main() {
    string s1("ababcedabf");
    string s2("bad");
    reverse(s1.begin(),s1.end());
    int ans = kmp(s1,s2);
    int sz1 = s1.size();
    cout << sz1-ans-1 << endl;
    return 0;
}

30.6 手写string的compare函数

要求：compare有连个参数const char* s1和const char *s2，当s1=s2时，返回0，当s1大于s2时返回-1，当s1小于s2时返回1

#include 
#include 
using namespace std;

int mycompare(const char *s1, const char *s2){
    assert(s1 != nullptr && s2 != nullptr);
    int k=0;
    while(s1[k] != '\0' && s2[k] != '\0' && s1[k] == s2[k]) ++k;
    if(s1[k] == '\0' && s2[k] == '\0') return 0;
    else if(s1[k] != '\0' && s2[k] == '\0') return -1;
    else if(s1[k] == '\0' && s2[k] != '\0') return 1;
    else if(s1[k] > s2[k]) return -1;
    else return 1;
}

int main() {
    char s1[] = "abc";
    char s2[] = "abc";
    char s3[] = "abd";
    char s4[] = "";
    char *s5 = nullptr;
    std::cout << mycompare(s1,s2) << std::endl;
    std::cout << mycompare(s1,s3) << std::endl;
    std::cout << mycompare(s1,s4) << std::endl;
    std::cout << mycompare(s1,s5) << std::endl;
    return 0;
}

结果如下：

30.7 手写哈希表

30.8 最长回文字符串

leetcode第5题，思路是中心扩散+考虑奇偶

class Solution {
public:
    string longestPalindrome(string s) {
        int sz =s.size();
        if(sz < 2) return s;
        int idx=0, max_len=0, j;
        for(int i=0; i<sz; ++i){
            j = 0;
            while(i-j >=0 && i+j < sz && s[i-j] == s[i+j]) ++j;
            --j;
            if(2*j+1 > max_len){
                max_len = 2*j+1;
                idx = i-j;
            }
            j=0;
            while(i-j>=0 && i+j+1 < sz && s[i-j] == s[i+j+1]) ++j;
            if(2*j > max_len){
                max_len = 2*j;
                idx = i-j+1;
            } C
        }
        string ans = s.substr(idx, max_len);
        return ans;
    }
};

30.9 归并排序

时间复杂度O(nlogn)，稳定，空间复杂度O(n)
子问题：对两个已经排好序的数组进行排序
再加上分治思想
可以使用递归完成

#include 
#include 
using namespace std;

// 现在[l,m)和[m,r]位置的元素都是有序的，merge将它们进行合并
void merge(vector<int> &nums, int l, int m, int r){
    int left_size = m-l;
    int right_size = r-m+1;
    vector<int> v_left(left_size);
    vector<int> v_right(right_size);
    // 复制两边有序的元素
    for(int i=l; i<m; ++i)C
        v_left[i-l] = nums[i];
    for(int i=m; i<=r; ++i)
        v_right[i-m] = nums[i];
    int k=l,i=0,j=0; // 注意k的初始值为l，而不是0
    while(i<left_size && j<right_size){
        if(v_left[i] < v_right[j]){
            nums[k++] = v_left[i++];
        }else{
            nums[k++] = v_right[j++];
        }
    }
    // 处理剩余元素
    while(i<left_size) nums[k++] = v_left[i++];
    while(j<right_size) nums[k++] = v_right[j++];
}

void mergeSort(vector<int> &nums, int l, int r){
    if(l == r) return;
    int mid = l + (r-l)/2;
    mergeSort(nums,l,mid);
    mergeSort(nums,mid+1,r);
    merge(nums,l,mid+1,r);
}
int main() {
    vector<int> v{6,8,10,9,4,5,3,4,2,6};
    mergeSort(v,0,v.size()-1);
    for(auto m : v)
        cout << m << " ";
    cout << endl;
    return 0;
}

30.10 已知先序和中序数组求后序遍历数组

思路：先用先序和中序恢复出原来的树，然后再进行后序遍历，求出结果即可
难点在于下一次递归前序起点和终点位置以及中序起点位置

#include 
#include 
#include 
using namespace std;

struct TreeNode{
    int val;
    TreeNode *left,*right;
    TreeNode(int n):val(n),left(nullptr),right(nullptr){}
};

TreeNode *createTree(vector<int> &pre,unordered_map<int, int> &mp,
                int pre_start, int pre_end, int in_start){
    if(pre_start>pre_end) return nullptr;
    int val = pre[pre_start];
    TreeNode *root = new TreeNode(val);
    int idx = mp[val];
    root->left = createTree(pre,mp,pre_start+1,pre_start+idx-in_start,in_start);
    root->right = createTree(pre,mp,pre_start+idx-in_start+1,pre_end,idx+1);
    return root;
}

void postOrder(TreeNode* root){
    if(root){
        postOrder(root->left);
        postOrder(root->right);
        cout << root->val << endl;
    }
}

int main() {
    vector<int> pre{1,2,6,3,4,5};
    vector<int> in{6,2,1,4,3,5};
    unordered_map<int,int> mp;
    for(int i=0; i<in.size(); ++i){
        mp[in[i]] = i;
    }
    TreeNode *root = createTree(pre,mp,0,pre.size()-1,0);
    postOrder(root);
    return 0;
}

30.11 写个memcpy()函数

注意点：参数类型(void *dst, const void *src, size_t sz)，返回值类型void *，正常拷贝(从前往后拷贝)，有重叠时（dst的前面一部分和src的后面一部分重叠，注意条件怎么写，注意需要强制类型转换后才可以用指针加常数，需要从后往前拷贝），注意dst或src存在空指针时返回空指针

void *mymemcpy(void *dst, const void *src, size_t sz){
    if(dst == nullptr || src == nullptr) return nullptr;
    if(src < dst && (char*)src+sz>(char*)dst){ //*dst前面一部分和*src后面一部分重叠，则采用从后往前拷贝的方式
        char *p1 = (char*)dst + sz - 1;
        char *p2 = (char*)src + sz - 1;
        while(sz--){
            *p1-- = *p2--;
        }
    }
    else{ // 正常情况下从前往后拷贝
        char *p1 = (char*) dst;
        char *p2 = (char*) src;
        while(sz--){
            *p1++ = *p2++;
        }
    }
    return dst;
}

30.12 写个二分查找

#include 
#include 
using namespace std;

int find(vector<int> &nums, int target){
    int l=0, r=nums.size()-1, mid;
    while(l<r){
        mid = l + (r-l)/2;
        if(nums[mid] < target) l = mid+1;
        else r = mid;
    }
    return l;
}

int main() {
    vector<int> nums{2,3,4,5,6,7,8,9};
    int target = 8;
    std::cout << find(nums,target) << std::endl;
    return 0;
}

30.13 宏定义

30.13.1 写一个标准宏MIN，这个宏输入两个参数返回较小的一个

注意点：参数用括号，使用三元运算符，但注意不是return，而是直接就是语句，一般宏要大写，不能以分号结尾

#define MIN(A,B) ((A) < (B) ? (A) : (B))

30.13.2 写一个宏，声明一个常数，表明1年中有多少秒

注意点：宏大写，使用乘法运算，括号，ul
#define SEC_PER_YEAR (3652460*60ul)

30.14 判断一棵树是否是平衡二叉树

思路：子问题：对于子树判断是否是平衡二叉树，若是返回当前子树的最大深度，否则返回0，结果通过引用传递

int dfs(TreeNode *root, bool &flag){
    if(root == nullptr || !flag) return 0;
    int l = dfs(root->left, flag);
    int r = dfs(root->right, flag);
    if(l-r<-1 || l-r>1){
        flag = false;
        return 0;
    }
    else{
        return 1+max(l,r);
    }
}
bool isBalanced(TreeNode* root) {
    bool flag = true;
    dfs(root, flag);
    return flag;
}

子问题：求一棵二叉树的最大深度

int maxDepth(TreeNode* root) {
    if(root == nullptr) return 0;
    return 1+max(maxDepth(root->left), maxDepth(root->right));
}

30.15 判断两个链表是否相交

思路：先求两个链表的长度，然后让长链表先走相差的步数，这样他们就会在一开始相交的地方相遇

ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
        int n1=0,n2=0;
        ListNode *cur = headA;
        while(cur){
            ++n1;
            cur = cur->next;
        }
        cur = headB;
        while(cur){
            ++n2;
            cur = cur->next;
        }
        // 以下保证,l1指向长链表，n1是长链表的长度，l2和n2正好相反
        ListNode *l1, *l2;
        if(n1 > n2){
            l1 = headA;
            l2 = headB;
        }
        else{
            l1 = headB;
            l2 = headA;
            int tmp = n1;
            n1 = n2;
            n2 = tmp;
        }

        int i=n1-n2;
        while(i--) l1 = l1->next;
        while(l1){
            if(l1 == l2) return l1;
            else{
                l1 = l1->next;
                l2 = l2->next;
            }
        }
        return nullptr;
    }

30.16 反转单链表

思路：利用三个指针，pre、cur、和tmp，注意pre初始值为nullptr，利用临时指针tmp实现局部反转，返回pre

ListNode* reverseList(ListNode* head) {
    ListNode *pre = nullptr, *cur = head, *tmp;
    while(cur){
        tmp = cur;
        cur = cur->next;
        tmp->next = pre;
        pre = tmp;
    }
    return pre;
}

30.17 二叉树的最近公共祖先

leetcode 236，思路：最关键是如何定义最近公共祖先？答：（1）左子树找到p且右子树找到q，或者左子树找到q且又子树找到p，这里注意到p和q都是树的结点，是唯一的，因此条件可以转换成左子树找到p或q且右子树也找到p或q（因为结点唯一，如果左子树找到p，右子树找到p或q，那么右子树找到的一定是q；同理，如果左子树找到q，右子树找到p或q，那么右子树找到的一定是p）（2）根就是p或q且左子树或者右子树有另外一个结点，由于结点的唯一性，这个同样可以转换成根结点找到p或q且左子树找到p或q或者右子树找到p或q。
另外答案使用全局变量存放，递归终止条件是根为空时，最终返回的是当前树是否存在p或q。
看到由于结点的唯一性，实际上我们可以不用区分子树找到的是q还是p，而只需要关心找到p或者q，因为一旦找到其他子树就不会找到，只可能找到另外一个目标结点

TreeNode *ans;
bool dfs(TreeNode *root, TreeNode *p, TreeNode *q){
    if(root == nullptr) return false;
    bool l = dfs(root->left, p, q);
    bool r = dfs(root->right, p, q);
    if(l&&r || ((root == p || root == q) && (l||q))) ans = root;
    return l || r || root == p || root == q;
}
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
    dfs(root,p,q);
    return ans;
}

30.18 两数相加

leetcode第二题，链表相加，可以模仿加法运算，注意进位的情况、指针为空的情况，已经最终是否还存在进位的情况

ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {
        ListNode *dummyHead = new ListNode(0);
        ListNode *cur = dummyHead, *p = l1, *q = l2;
        int carry = 0;
        while(p || q){
            int val1 = p ? p->val : 0;
            int val2 = q ? q->val : 0;
            int ans = val1 + val2 + carry;
            carry = ans>=10 ? 1 : 0;
            cur->next = new ListNode(ans%10);
            cur = cur->next;
            p = p ? p->next : nullptr;
            q = q ? q->next : nullptr;
        }
        if(carry){
            cur->next = new ListNode(1);
        }
        return dummyHead->next;
    }

31 double free

两次free同一个指针会导致这个问题，可能导致堆地址泄漏

32 什么是野指针？怎么避免野指针

产生野指针的原因：

• 定义的指针没有初始化
• 释放内存后没有将指针置空

避免的方式：

• 定义指针时初始化
• 释放内存后将指针置空

33 struct对齐

struct A
{
  char a;
  int b;
  char c;
  double d;
};

占用几个字节？
答案是24

34 内存有哪些区

答：代码区、静态区、栈区、堆区

35 浏览器url的整个过程

（1）域名解析（获得IP），浏览器DNS缓存-》操作系统DNS-》域名服务器
（2）应用层（http）
（3）传输层(tcp 三次握手)
（4）网络层(路由，ARP)
（5）链路层（封装成帧）
服务器传回数据，浏览器渲染

36 软链接、硬链接

硬链接： 可以将它理解为一个 “指向原始文件 inode 的指针”，系统不为它分配独立的 inode 和 文件。所以，硬链接文件与原始文件其实是同一个文件，只是名字不同。
软链接： 等同于 Windows 系统下的快捷方式。仅仅包括所含链接文件的路径名字。因此能链接目录，也能跨文件系统链接。但是，当删除原始文件后，链接文件也将失效。

37 什么是指针？

指针是指向另外一种类型的符合类型，可以实现对其他对象的间接访问，指针里面存放指向的对象的地址。

38 指针和引用的区别

1、指针有自己的一块空间，而引用只是一个别名
2、sizeof()时，指针的结果是4，引用的结果是被引用对象占用字节数
3、指针初始化可以为NULL，而引用必须初始化并且必须是一个已有对象的引用
4、存在多级指针，但是只有一级引用
5、参数传递时，函数中指针必须通过解引用才能操作原来的对象，而引用直接就可以操作原来对象
6、动态分配内存时返回的必须是指针，如果返回引用会出现内存泄漏
7、指针在使用中可以指向其他对象，但是引用只能是一个对象的引用，不能更改
8、指针和引用++ --的意义不同

39 自旋锁和互斥锁

互斥锁：
最常使用于线程同步的锁；标记用来保证在任一时刻，只能有一个线程访问该对象，同一线程多次加锁操作会造成死锁；临界区和互斥量都可用来实现此锁，通常情况下锁操作失败会将该线程睡眠等待锁释放时被唤醒。
在多任务操作系统中，同时运行的多个任务可能都需要使用同一种资源。互斥锁是一种简单的加锁的方法来控制对共享资源的访问，互斥锁只有两种状态,即上锁( lock )和解锁( unlock )。
（1）. 原子性：把一个互斥量锁定为一个原子操作，这意味着操作系统（或pthread函数库）保证了如果一个线程锁定了一个互斥量，没有其他线程在同一时间可以成功锁定这个互斥量；
（2）. 唯一性：如果一个线程锁定了一个互斥量，在它解除锁定之前，没有其他线程可以锁定这个互斥量；
（3）. 非繁忙等待：如果一个线程已经锁定了一个互斥量，第二个线程又试图去锁定这个互斥量，则第二个线程将被挂起（不占用任何cpu资源），直到第一个线程解除对这个互斥量的锁定为止，第二个线程则被唤醒并继续执行，同时锁定这个互斥量。

自旋锁：
自旋锁与互斥锁有点类似，只是自旋锁不会引起调用者睡眠，如果自旋锁已经被别的执行单元保持，调用者就一直循环在那里看是否该自旋锁的保持者已经释放了锁，"自旋"一词就是因此而得名。其作用是为了解决某项资源的互斥使用。因为自旋锁不会引起调用者睡眠，所以自旋锁的效率远高于互斥锁。虽然它的效率比互斥锁高，但是它也有些不足之处：
1、自旋锁一直占用CPU，他在未获得锁的情况下，一直运行－－自旋，所以占用着CPU，如果不能在很短的时间内获得锁，这无疑会使CPU效率降低。
2、在用自旋锁时有可能造成死锁，当递归调用时有可能造成死锁，调用有些其他函数也可能造成死锁，如 copy_to_user()、copy_from_user()、kmalloc()等。
因此我们要慎重使用自旋锁，自旋锁只有在内核可抢占式或SMP的情况下才真正需要，在单CPU且不可抢占式的内核下，自旋锁的操作为空操作。自旋锁适用于锁使用者保持锁时间比较短的情况下。

39.1 自旋锁在抢占和非抢占、单核和多核中的区别

1. 在单cpu，不可抢占内核中，自旋锁为空操作。
2. 在单cpu，可抢占内核中，自旋锁实现为“禁止内核抢占”，并不实现“自旋”。
3. 在多cpu，可抢占内核中，自旋锁实现为“禁止内核抢占” + “自旋”。
4. 因为在多核抢占的情况下，使用自旋锁会禁止内核抢占，这样多核抢占就相当于多核非抢占的情况。

抢占式内核与非抢占式内核：
在非抢占式内核中，如果一个进程在内核态运行，其只有在以下两种情况会被切换：

1. 其运行完成（返回用户空间）
2. 主动让出cpu（即主动调用schedule或内核中的任务阻塞——这同样也会导致调用schedule）

在抢占式内核中，如果一个进程在内核态运行，其只有在以下四种情况会被切换：

1. 其运行完成（返回用户空间）
2. 主动让出cpu（即主动调用schedule或内核中的任务阻塞——这同样也会导致调用schedule）
3. 当从中断处理程序正在执行，且返回内核空间之前（此时可抢占标志premptcount须为0） 。
4. 当内核代码再一次具有可抢占性的时候，如解锁及使能软中断等。

可能发生死锁的情况：
首先，对于多核抢占与多核非抢占的情况，在使用自旋锁时，其情况基本是一致的。
因为在多核抢占的情况下，使用自旋锁会禁止内核抢占，这样多核抢占就相当于多核非抢占的情况。

那下面就只分析多核非抢占的情况。
假设系统有A，B两个CPU。
A上正在运行的a进程已获得自旋锁，并在临界区运行。
B上正在运行的b进程企图获得自旋锁，但由于自旋锁已被占用，于是b进程在B CPU上“自旋”空转。

这时，如果在A上的a进程因程序阻塞，而被休眠。接着A会切换运行另一进程c。
若这个进程c也企图获取自旋锁，c进程同样会因为锁已被占用，而在A上“自旋”空转。
这时候，A上的a进程与c进程就形成了死锁。a进程需要被c进程占用的CPU,c进程需要被a进程占用的锁。

至于在单cpu内核上不会出现上述情况，因为单cpu上的自旋锁实际没有“自旋功能”。

40 sizeof和strlen的区别

sizeof是计算类型所占空间的字节数，它是一个运算符，可以以类型、函数、变量作为参数，结果类型是size_t，sizeof是在编译时就计算出来结果；
strlen是计算字符串的长度，但不包括’\0’，要求字符串或者说字符数组必须以’\0’结尾，它是一个函数，在运行时得到结果。

41 已知一个变量的地址如何求结构体的首地址

思路：计算该变量到结构体首地址的偏移量，然后用这个变量的地址减去这个偏移量就可以得到结果
计算偏移量的代码：&(((A*)0)->i)，注意这里0表示当结构体起始位置为0时，计算出i的地址，也就是i相对于结构体起始位置的偏移量
然后实现过程中需要考虑转成char *格式

#include "stdio.h"
struct A{
    char a;
    int i;
    char b;
};

int main() {
    A test;
    printf("%p\n",&test.i);
    char *offset = (char*)&(((A*)0)->i);
    printf("%p\n",offset);
    char *ans = (char*)((char*)(&test.i) - offset);
    printf("%p\n",ans);
    return 0;
}

42 面试中常见的特殊树

42.1 平衡二叉树（AVL）

是一个空树或者左子树和右子树的高度差不超过1的树，且对于每个子树都是这样。

42.2 满二叉树

定义：树的每一层节点数都达到最大值，那么它就是满二叉树

42.3 完全二叉树

定义：除了最后一层，其它层的结点都是满的，而且最后一层的结点是从左到右连续排列的