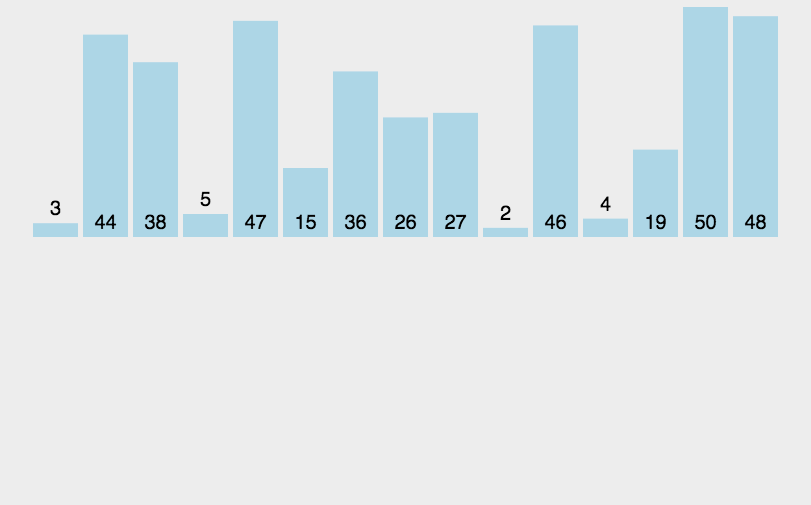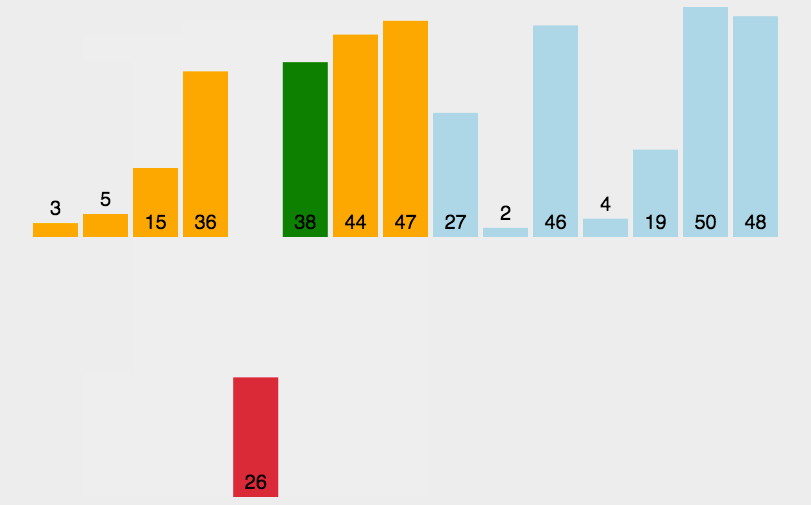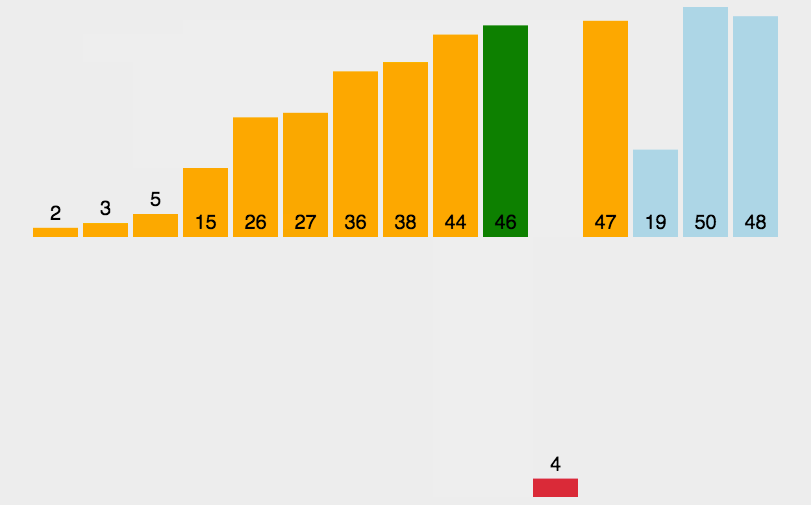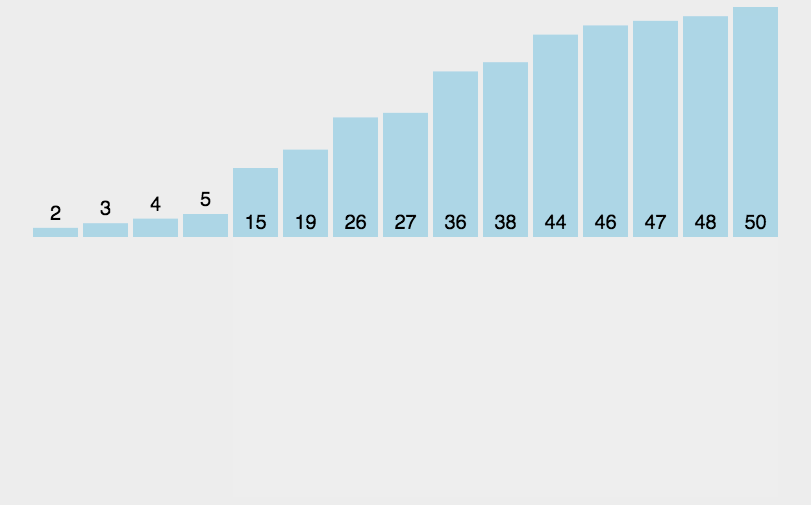
基础数据结构---八大排序

排序 : 笔试和面试的重点.1.算法描述;2.实现;3.效率分析(时间复杂度,空间复杂度,稳定性)
难点 : 排序算法太多
稳定性 : 针对关键字相同的数据(相同的数字),排序前如果A在A’的前面,排序后还能保证A在A’的前面则算法稳定,否则不稳定；有没有跳跃的交换数据,有则不稳定,没有则稳定

---

第一个排序:(简单)直接插入排序.特点 数据越有序越快,完全有序则为O(n)
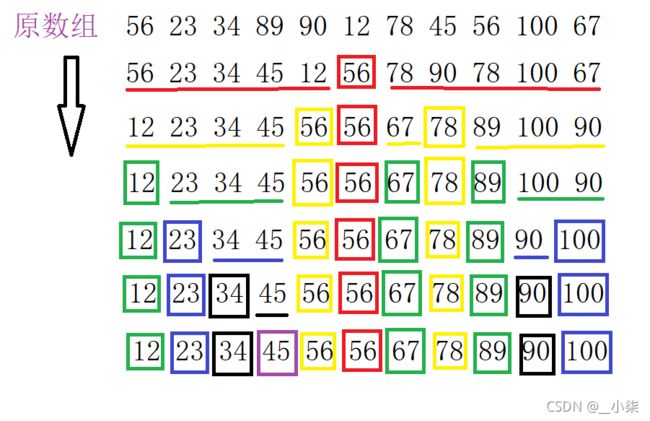
第二个排序:希尔(Shell)排序.间隔式的分组,利用插入排序让组内有序,然后缩小分组再排序直到组数为1则全部有序
第三个排序:冒泡排序.两两比较,大的往后
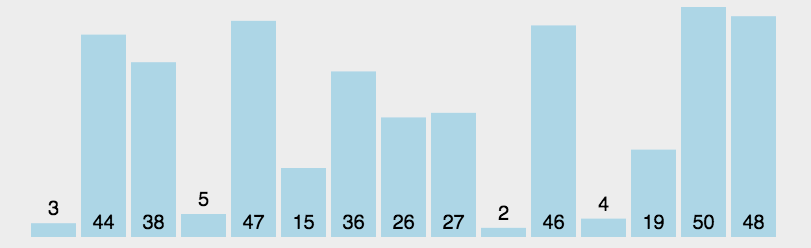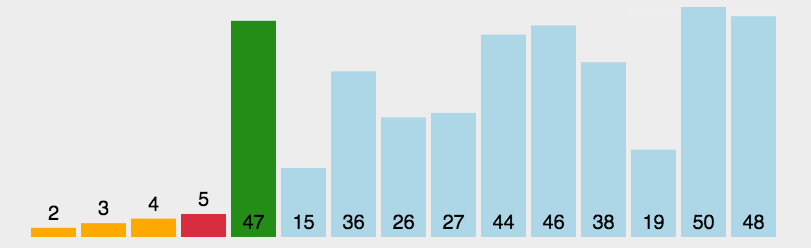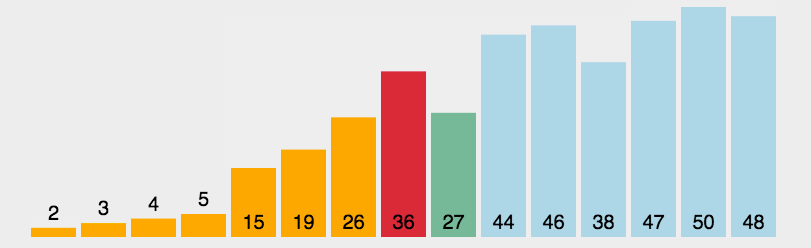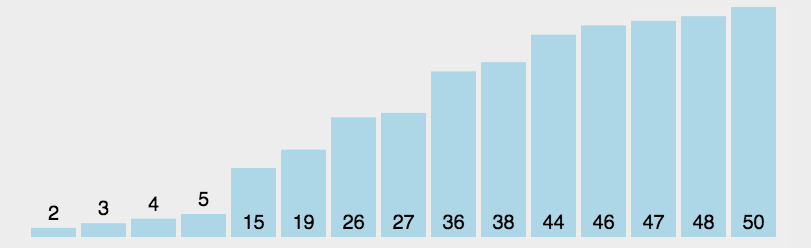
第四个排序:快速排序.找到一个基准(第一个数据),
1.从后往前找比基准小的数据往前移,2.从前往后找比基准大的数据往后移.3,重复1,2直到找到基准位置
快速排序的缺点:1.越有序越慢,完全有序则为O(n^2);2.空间复杂度为O(logn)不是O(1);3.不稳定;
第五个排序:选择排序.每次从待排序中找到最小值和待排序的第一个交换
第六个排序:堆排序
第七个排序:2路归并排序.将两段有序的数据合并成一段有序的数据,直到所有的数据有序
第八个排序:基数(桶)排序,低位优先,将所有的数字,从低位(个位)开始到高位,依次进相应的队列,再出,直到全部有序

1.（简单）直接插入排序

实现：

//(简单)直接插入排序
//(简单)直接插入排序.特点 数据越有序越快,完全有序则为O(n)

void InsertSort(int* arr, int len)//O(n^2),O(1),稳定
{//没有交换数据,稳定
	int tmp;
	int j;
	for (int i = 1; i < len; i++)//i当前需要处理的数字的下标
	{
		tmp = arr[i];
		for (j = i - 1; j >= 0; j--)//从后往前找位置,并同时移动数据
		{
			if (arr[j] > tmp)//该数据需要后移
			{
				arr[j + 1] = arr[j];
			}
			else
			{
				break;
			}
		}
		arr[j + 1] = tmp;
	}
}

2.希尔（shell）排序

每一趟分为n组
每一组用直接插入排序

//希尔(Shell)排序.间隔式的分组,利用插入排序让组内有序,然后缩小分组再排序直到组数为1则全部有序


//一趟shell过程,gap为组数(间隔)
static void Shell(int* arr, int len, int gap)
{
	int tmp;
	int j;
	for (int i = gap; i < len; i++)//从"第二个"数据开始
	{
		tmp = arr[i];
		for (j = i - gap; j >= 0; j -= gap)//和同组的数据比
		{
			if (arr[j] > tmp)
			{
				arr[j + gap] = arr[j];
			}
			else
			{
				break;
			}
		}
		arr[j + gap] = tmp;
	}
}

void ShellSort(int* arr, int len)//O(n^1.3 ~n^1.5),O(1),不稳定
{
	int d[] = { 5,3,1 };//分组数,最后一个一定为1
	for (int i = 0; i < sizeof(d) / sizeof(d[0]); i++)
	{
		Shell(arr, len, d[i]);
	}
}

3.冒泡排序

//冒泡排序,两两比较,大的往后
void BubbleSort(int* arr, int len)//O(n^2),O(1),稳定
{
	int tmp;
	for (int i = 0; i < len - 1; i++)//趟数
	{
		for (int j = 0; j + 1 < len - i; j++)//注意j+1越界
		{
			if (arr[j] > arr[j + 1])//交换
			{
				tmp = arr[j];
				arr[j] = arr[j + 1];
				arr[j + 1] = tmp;
			}
		}
	}
}

4.快速排序

//快速排序.找到一个基准(第一个数据),
//	   1.从后往前找比基准小的数据往前移,2.从前往后找比基准大的数据往后移.3,重复1,2直到找到基准位置
//	   快速排序的缺点:1.越有序越慢,完全有序则为O(n^2);2.空间复杂度为O(logn)不是O(1);3.不稳定;



//快速排序的一次划分
int Partition(int* arr, int low, int high)//O(n),O(1)
{
	int tmp = arr[low];//基准

	while (low < high)
	{
		//从后往前找比基准小的数据,往前移
		while (low<high && arr[high]>tmp)
			high--;
		if (low < high)
			arr[low] = arr[high];
		//从前往后找比基准大的数据,往后移
		while (low < high && arr[low] <= tmp)
			low++;
		if (low < high)
			arr[high] = arr[low];
	}
	arr[low] = tmp;
	return low;
}

void Quick(int* arr, int low, int high)
{
	int par = Partition(arr, low, high);
	if (low < par - 1)//左边数据超过一个
	{
		Quick(arr, low, par - 1);
	}
	if (par + 1 < high)
	{
		Quick(arr, par + 1, high);
	}
}

void QuickSort(int* arr, int len)//O(nlogn),O(logn),不稳定
{
	Quick(arr, 0, len - 1);
}

void Show(int* arr, int len)
{
	for (int i = 0; i < len; i++)
	{
		printf("%d ", arr[i]);
	}
	printf("\n");
}

5.选择排序

//选择排序.每次从待排序中找到最小值和待排序的第一个交换


//选择排序
void SelectSort(int* arr, int len)//O(n^2),O(1),不稳定 
{
	int minIndex;//最小值的下标
	int tmp;
	for (int i = 0; i < len - 1; i++)
	{
		minIndex = i;
		for (int j = i + 1; j < len; j++)//找最小值
		{
			if (arr[minIndex] > arr[j])//注意和书本区分,本代码没有交换,全部找完后再交换
			{
				minIndex = j;
			}
		}
		if (minIndex != i)//最小值和待排序的第一个值交换
		{
			tmp = arr[minIndex];
			arr[minIndex] = arr[i];
			arr[i] = tmp;
		}
	}
}

6.堆排序

//堆调整
//从上往下调整,start起始下标,end结束下标
void HeapAdjust(int* arr, int start, int end)//O(logn)
{
	int tmp = arr[start];
	for (int i = 2 * start + 1; i <= end; i = 2 * i + 1)
	{
		if (i < end && arr[i] < arr[i + 1])//有右孩子,且左孩子的值小于右孩子
			i++;//i一定是左右孩子较大值的下标
		if (arr[i] > tmp)
		{
			arr[start] = arr[i];
			start = i;
		}
		else //找到位置了
			break;
	}
	arr[start] = tmp;
}

//父->子:i->2i+1,2i-1
//子->父:i->(i-1)/2
//堆排序
void HeapSort(int* arr, int len)//O(nlogn),O(1),不稳定
{
	//第一次建大根堆,从后往前,多次调整
	int i;
	for (i = (len - 1 - 1) / 2; i >= 0; i--)//从最后一棵子树开始 O(nlogn)
	{
		HeapAdjust(arr, i, len - 1);
	}

	//每次将根和待排序的最后一个交换,然后再调整
	int tmp;
	for (i = 0; i < len - 1; i++) //O(nlogn)
	{
		//交换
		tmp = arr[0];
		arr[0] = arr[len - 1 - i];
		arr[len - 1 - i] = tmp;

		//再调整
		HeapAdjust(arr, 0, len - 1 - i - 1);
	}
}

7.归并排序

//2路归并排序.将两段有序的数据合并成一段有序的数据,直到所有的数据有序


//一次归并
//gap:归并段的长度
static void Merge(int* arr, int len, int gap)//O(n),O(n)
{
	int low1 = 0;//第一个归并段的起始下标
	int high1 = low1 + gap - 1;//第一个归并段的结束下标
	int low2 = high1 + 1;//第二个归并段的起始下标
	int high2 = low2 + gap < len ? low2 + gap - 1 : len - 1;//第二个归并段的结束下标
	int* brr = (int*)malloc(len * sizeof(int));//存放归并好的数据
	int i = 0;//brr下标
	assert(brr != NULL);

	//有两个归并段
	while (low2 < len)
	{
		//两个归并段都还有数据,需要比
		while (low1 <= high1 && low2 <= high2)
		{
			if (arr[low1] <= arr[low2])
			{
				brr[i++] = arr[low1++];
			}
			else
			{
				brr[i++] = arr[low2++];
			}
		}

		//一个归并段的数据已经完成,另一个还有数据
		while (low1 <= high1)
		{
			brr[i++] = arr[low1++];
		}
		while (low2 <= high2)
		{
			brr[i++] = arr[low2++];
		}

		//下两个归并段
		low1 = high2 + 1;
		high1 = low1 + gap - 1;
		low2 = high1 + 1;
		high2 = low2 + gap < len ? low2 + gap - 1 : len - 1;
	}

	//只有一个归并段
	while (low1 < len)
	{
		brr[i++] = arr[low1++];
	}

	//将归并好的数据拷贝到arr中
	for (i = 0; i < len; i++)
	{
		arr[i] = brr[i];
	}
	free(brr);
}

//归并排序
void MergeSort(int* arr, int len)//O(nlogn),O(n),稳定
{
	for (int i = 1; i < len; i *= 2)
	{
		Merge(arr, len, i);
	}
}

8.基数排序

//基数(桶)排序,低位优先,将所有的数字,从低位(个位)开始到高位,依次进相应的队列,再出,直到全部有序


//获取最大数字的位数
static int GetFigur(int* arr, int len)
{
	int max = arr[0];//最大值
	for (int i = 1; i < len; i++)
	{
		if (max < arr[i])
			max = arr[i];
	}
	//987->3  丢个位  n /= 10
	int count = 0;
	while (max != 0)
	{
		count++;
		max /= 10;
	}
	return count;
}

//获取十进制整数右数第figur位的数figur从0开始,
//例如(123,0)->3;(123,1)->2;(123,2)->1;(123,3)->0
static int GetNum(int n, int figur)
{
	for (int i = 0; i < figur; i++)
		n /= 10;
	return n % 10;
}

//基数排序
void RadixSort(int* arr, int len)//O(d*n) d表示数据的位数   O(n) ,稳定    
{
	//需要利用10个队列,存放进队的数字
	SqQueue queArr[10];
	for (int i = 0; i < 10; i++)
	{
		InitQueue(&queArr[i]);
	}
	//得到最大数字的位数,确定进队和出队的趟数
	int count = GetFigur(arr, len);
	int index;//队列的下标
	for (int i = 0; i < count; i++)//处理每个数字从右往左的第i个数
	{
		for (int j = 0; j < len; j++)//遍历数组,并入队
		{
			index = GetNum(arr[j], i);//index保存arr[j]应该进入的队列下标
			Push(&queArr[index], arr[j]);//将数字存放到对应的队列
		}

		//所有数据出队.依次将所有队列的数据出队
		int j = 0;//arr下标
		for (int k = 0; k < 10; k++)//所有的队列
		{
			//一个队列可能有多个数据
			while (!IsEmpty(&queArr[k]))
			{
				Pop(&queArr[k], &arr[j++]);
			}
		}
	}
	for (int i = 0; i < 10; i++)
	{
		Destroy(&queArr[i]);
	}
}