✔★ 算法基础笔记(Acwing)(五)—— 动态规划【java版本】
动态规划
- 一、背包问题
-
-
-
-
- ★f[i][j] 背包容量为j,前i个物品的最大价值
- 1. 01背包问题(不需要初始化) ✔1.6 ✔1.7
- 2. ☆ 完全背包问题(后面的 = 前面的某一项的最大值)
-
-
- 一、朴素做法(三重循环)
- 二、二维数组的优化(理解f[i-1][j-k*v[i]]+w[i] 等价于 f[i][j-v[i]]+w[i])
- 三、一维数组的优化
-
- 3. 多重背包问题 I ✔1.6
- 4. ☆多重背包问题 II ✔1.6
-
-
- s = 1 + 2 + 4 + 8
-
- 5. 分组背包问题 ✔1.6
-
-
-
- 二、线性DP
-
-
-
- 1. 数字三角形 ✔1.6
- 2. 最长上升子序列
-
-
- 双重循环
- f[i] 以第i个数结尾的 上升子序列的最大值
-
- 3. 最长上升子序列 II
-
-
- ★★★★★f[i] 存储 最长上升子序列的 示范串
- ★★★★★ 二分 + dp优化
-
- 4. 最长公共子序列
-
-
- ★f[i][j]表示a的前i个字母,和b的前j个字母的最长公共子序列长度
- 思路 (在推导示例时,可以总结出)
-
- 5. 最短编辑距离
-
-
- ★f[i][j] 所有把a中的前i个字母 变成 b中前j个字母的集合的操作集合
- 做题总结
-
- 6. 编辑距离( 和上题差不多 )
-
-
- 三、区间dp
-
-
-
- 1. ☆ 石子合并
-
-
- ★f[i][j]表示将 i 到 j 合并的最小值
-
-
-
- 四、计数类DP
-
-
-
- 1. ☆ 整数划分
-
-
- ★f[i][j] 表示 背包为j的 前i个物品 的方案数
- 方案数 = 拿了i的方案数 + 没拿i的方案数
-
-
-
- 五、数位统计dp
-
-
-
- ★1. 计数问题
-
-
- 六、状态压缩DP
-
-
-
- 1. 蒙德里安的梦想
-
-
- ★f[i][j] 表示已经将前 i -1 列摆好,且从第i−1列,伸出到第 i 列的状态是 j 的所有方案
-
- 2. 最短Hamilton路径
-
-
- ★f[i][j] 所有从0走到j,所用的点是i的状态的所有路径.
-
-
-
- 七、树形DP
-
-
-
- 1. ☆ 没有上司的舞会
-
-
- ★f[i][0]所有以u为根的子树中选择,并且不选这个点的方案
- ★f[i][1]所有以u为根的子树中选择,选这个点的方案
-
-
-
- 八、记忆化搜索
-
-
-
- 1. 滑雪
-
-
- ★f[i][j] 以(i,j)开始的路径最大值
-
-
-
一、背包问题
★f[i][j] 背包容量为j,前i个物品的最大价值
1. 01背包问题(不需要初始化) ✔1.6 ✔1.7
原题链接
f[i][j]怎么想出来
在j体积下 前i个物品的最大价值
一、为什么要从0到v把背包中各种体积下的情况都存储下来呢?(算法理解)
因为我们需要回溯
二、但我们选i的时候,需要明白两件事
选不选第i件物品的判断依据
- 当 背包中限定的体积,小于v【i】一定不能选
- 当 背包中限定的体积可以装下v[i]时,那么我们就需要知道,到底装下这个价值大,还是不装下这个价值大
装下的价值 = f[i-1][j-v[i]] + w[i]
不装下的价值 = f[i-1][j];
总结:深刻记住 f[i][j] 表示 在j体积中前i个物品下的最大价值
二维
import java.util.*;
public class Main {
static final int N = 1010;
static int n,m;
static int[] w = new int[N];
static int[] v = new int[N];
static int[][] f = new int[N][N];
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
n = scanner.nextInt();
m = scanner.nextInt();
for (int i = 1; i <= n; i++) {
v[i] = scanner.nextInt();
w[i] = scanner.nextInt();
}
for (int i = 1; i <= n; i++) {
for (int j = 0; j <= m; j++) {
if (v[i] > j) {
f[i][j] = f[i-1][j];
} else {
f[i][j] = Math.max(f[i-1][j],f[i-1][j-v[i]] + w[i]);
}
}
}
System.out.print(f[n][m]);
}
}
一维
import java.util.*;
public class Main {
static final int N = 1010;
static int n,m;
static int[] w = new int[N];
static int[] v = new int[N];
static int[] f = new int[N];
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
n = scanner.nextInt();
m = scanner.nextInt();
for (int i = 1; i <= n; i++) {
v[i] = scanner.nextInt();
w[i] = scanner.nextInt();
}
for (int i = 1; i <= n; i++) {
for (int j = m; j >= 0; j--) {
if (v[i] > j) {
f[j] = f[j];
} else {
f[j] = Math.max(f[j],f[j-v[i]] + w[i]);
}
}
}
System.out.print(f[m]);
}
}
2. ☆ 完全背包问题(后面的 = 前面的某一项的最大值)
f[i , j ] = max( f[i-1,j] , f[i-1,j-v]+w , f[i-1,j-2*v]+2*w , f[i-1,j-3*v]+3*w , .....)
f[i , j-v]= max( f[i-1,j-v] , f[i-1,j-2*v] + w , f[i-1,j-3*v]+2*w , .....)
原题链接![]()
一、朴素做法(三重循环)
import java.util.*;
public class Main {
static int N = 1010;
static int n,m;
static int[] v = new int[N];
static int[] w = new int[N];
static int[][] f = new int[N][N];
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
n = scanner.nextInt();
m = scanner.nextInt();
for (int i = 1; i <= n; i++) {
v[i] = scanner.nextInt();
w[i] = scanner.nextInt();
}
for (int i = 1; i <= n; i++) {
for (int j = 0; j <= m; j++) {
if (j < v[i]) {
f[i][j] = f[i-1][j];
} else {
for (int k = 0; k*v[i] <= j; k++) {
f[i][j] = Math.max(f[i][j],f[i-1][j-k*v[i]] + k*w[i]);
}
}
}
}
System.out.print(f[n][m]);
}
}
二、二维数组的优化(理解f[i-1][j-k*v[i]]+w[i] 等价于 f[i][j-v[i]]+w[i])
import java.util.*;
public class Main {
static int N = 1010;
static int n,m;
static int[] v = new int[N];
static int[] w = new int[N];
static int[][] f = new int[N][N];
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
n = scanner.nextInt();
m = scanner.nextInt();
for (int i = 1; i <= n; i++) {
v[i] = scanner.nextInt();
w[i] = scanner.nextInt();
}
for (int i = 1; i <= n; i++) {
for (int j = 0; j <= m; j++) {
if (j < v[i]) {
f[i][j] = f[i-1][j];
} else {
f[i][j] = Math.max(f[i-1][j],f[i][j-v[i]] + w[i]);
}
}
}
System.out.print(f[n][m]);
}
}
三、一维数组的优化
#include二维
#include一维
import java.util.*;
public class Main {
static int N = 1010;
static int n,m;
static int[] v = new int[N];
static int[] w = new int[N];
static int[] f = new int[N];
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
n = scanner.nextInt();
m = scanner.nextInt();
for (int i = 1; i <= n; i++) {
v[i] = scanner.nextInt();
w[i] = scanner.nextInt();
}
for (int i = 1; i <= n; i++) {
for (int j = 0; j <= m; j++) {
if (j < v[i]) {
f[j] = f[j];
} else {
f[j] = Math.max(f[j],f[j-v[i]] + w[i]);
}
}
}
System.out.print(f[m]);
}
}
怎么由二维变成一维
看更新f[i][j] 需要的是本行数据还是上行数据
3. 多重背包问题 I ✔1.6
原题链接
三重循环(针对的是f[i][j]处理)
★不需要处理j不够的情况
import java.util.*;
public class Main{
public static void main(String[] args){
Scanner scan = new Scanner(System.in);
int N = 110;
int[] v = new int[N],w = new int[N],s = new int[N];
int[][] f = new int[N][N];
int n = scan.nextInt();
int m = scan.nextInt();
for(int i = 1 ; i <= n ; i ++ ){
v[i] = scan.nextInt();
w[i] = scan.nextInt();
s[i] = scan.nextInt();
}
for(int i = 1 ; i <= n ; i ++ )
for(int j = 0 ; j <= m ; j ++ )
for(int k = 0 ; k <= s[i] && k * v[i] <= j; k ++ )
f[i][j] = Math.max(f[i][j], f[i - 1][j - k * v[i]] + k * w[i]);
System.out.println(f[n][m]);
}
}
4. ☆多重背包问题 II ✔1.6
s = 1 + 2 + 4 + 8
原题链接
import java.util.*;
public class Main{
public static void main(String[] ags){
Scanner scan = new Scanner(System.in);
int N = 12000;
//为什么是12000呢,
//因为是二进制,一个数最多就是2的12次方就会超过题目给的2000,所以给个将限制范围1000*12
int[] v = new int[N];
int[] w = new int[N];
int[] f = new int[N];
int n = scan.nextInt();
int m = scan.nextInt();
int cnt = 0;
for(int i = 0 ; i < n ; i ++ ){
int a = scan.nextInt();
int b = scan.nextInt();
int s = scan.nextInt();
int k = 1; // 相当于一开始给了个2的0次幂
//这一步是将每一个s都分解成2的次幂个组合
while(s >= k){
cnt ++ ;
v[cnt] = a * k; //选择多少个数每一个都乘上
w[cnt] = b * k; //同上
s -= k; // s 分解成2的0到k次 幂(小于s),
k *= 2; // k每次都成2,就是2的倍数
}
//比如10,分成 1 2 4 如果加上8加能够凑出1-15个数,所以超过10,所以我们用10减去前面的数,剩下3
//所以分成 1 2 4 3
//下面这一步就是判断生下来的数是多少
if(s > 0){
cnt ++;
v[cnt] = a * s;
w[cnt] = b * s;
}
}
n = cnt; // 将所有组合的值赋值给n
//用01背包模板来完成这个选择,
//01背包是前i个物品中选,总体积不超过j
//这里是将每一种可能对应01背包,演变成01背包问题,不是 像 完全背包 那样所有的可能在一起计算,
//比如f[i][j],前i个物品中选,不包含i还有包含1个i来比较最大值,,不包含i和包含两个i来比较最大值 以此类推
//这样来判断
for(int i = 1 ; i <= n ; i ++ )
for(int j = m ; j >= v[i] ; j --)
f[j] = Math.max(f[j],f[j - v[i]] + w[i]);
System.out.println(f[m]);
}
}
5. 分组背包问题 ✔1.6
原题链接
二维
#include一维
#include 二、线性DP
1. 数字三角形 ✔1.6
★f[i][j] 从下到上 走到f[i][j]的所有路径的最大值
原题链接
原题链接
![]()
import java.util.*;
public class Main{
public static void main(String[] args){
Scanner scan = new Scanner(System.in);
int N = 510;
int[][] w = new int[N][N];
int[][] f = new int[N][N];
int n = scan.nextInt();
for(int i = 1 ; i <= n ; i ++ ){
for(int j = 1 ; j <= i ; j ++ ){
w[i][j] = scan.nextInt();
}
}
//f存的是每一个路劲上面和的最大值
for(int i = 1 ; i <= n ; i ++ ) f[n][i] = w[n][i];
// 我们从下面往上面把遍历,所以最先面一排的f表示的就是当前点的最大值,赋值上权值
//从下面往上面遍历,因为我们最底层已经赋值了,所以从n - 1层开始,逐层递减到1
for(int i = n - 1 ; i != 0 ; i -- ){
//在第几层就有几个数,所以j是表示个数 ,从左到右
for(int j = 1 ; j <= i ; j ++ ){
//每一个比较他的左下边的点的路劲的最大值
//右边点的路劲的最大值,进行一个max
f[i][j] = Math.max(f[i + 1][j] + w[i][j] , f[i + 1][j + 1] + w[i][j]);
}
}
//最后输出顶点的路径的最大值
System.out.println(f[1][1]);
}
}
2. 最长上升子序列
双重循环
f[i] 以第i个数结尾的 上升子序列的最大值
原题链接
![]()
import java.util.*;
public class Main {
static int D = 1010;
static int N;
static int nums[] = new int[D];
static int f[] = new int[D];
static int ans = 0;
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
N = scanner.nextInt();
for (int i = 1; i <= N; i++) nums[i] = scanner.nextInt();
nums[0] = -0x3f3f3f3f;
for (int i = 1; i <= N; i++) {
for (int j = 0; j < i; j++) {
if (nums[j] < nums[i]) {
f[i] = Math.max(f[i],f[j] + 1);
ans = Math.max(ans,f[i]);
}
}
}
System.out.print(ans);
}
}
3. 最长上升子序列 II
★★★★★f[i] 存储 最长上升子序列的 示范串
★★★★★ 二分 + dp优化
原题链接
import java.util.*;
public class Main{
public static void main(String[] args){
Scanner scan = new Scanner(System.in);
int N = 100010;
int[] a = new int[N];//输入的数列
int[] q = new int[N];//每种长度的最长上升子序列中结尾的最小值
int n = scan.nextInt();
for(int i = 0 ; i < n ; i ++ ){
a[i] = scan.nextInt();
}
int len = 0;//一开始长度是0;
q[0] = (int)-2e9; //确保每个数都能够找到一个比他小的数,然后接在其后面
//一个数可以接在什么位置,用二分来寻找每种长度的结尾的最小值比这个数小的的位置,然后长度加1,
//就是新的最长上升子序列的长度
for(int i = 0 ; i < n ; i ++ ){
int l = 0,r = len;
while(l < r){
int mid = l + r + 1 >> 1;
if(q[mid] < a[i]) l = mid;
else r = mid - 1;
}
//找到位置之后更新长度
len = Math.max(len, r + 1);
//比如因为找到的数q[4]是小于的a最大的数,所以后面的一个数q[5]就是大于等于这个数
//然后我们可以接在q[4]后面,所以现在长度是5,变成q[5],然后因为我们的这个数是小于或者等于q[5]
//所以直接将值赋上就行
q[r + 1] = a[i];
}
System.out.println(len);
}
}
4. 最长公共子序列
★f[i][j]表示a的前i个字母,和b的前j个字母的最长公共子序列长度
原题链接
![]()
思路 (在推导示例时,可以总结出)
- f[i][j] 表示什么需要先想清楚。
表示的是:在i,j组合的情况下,的最大子串 长度
所以当 i,j相等时
f[i][j] = f[i-1][j-1] + 1
不相等的时候
f[i][j] = max(f[i-1][j],f[i][j-1]);
import java.util.*;
public class Main{
public static void main(String[] args){
Scanner scan = new Scanner(System.in);
int N = 1010;
char[] a = new char[N];
char[] b = new char[N];
int[][] f = new int[N][N];
int n = scan.nextInt();
int m = scan.nextInt();
String A = scan.next();
String B = scan.next();
for(int i = 1 ; i <= n ; i ++ ) a[i] = A.charAt(i - 1);
for(int i = 1 ; i <= m ; i ++ ) b[i] = B.charAt(i - 1);
//本来还有一种方案就是ai和bj都不包含
//包含ai不包含bj --和-- 不包含ai包含bj 这两种方案已经包含了上面的所有可能
//所以不用重复比较,省略
for(int i = 1 ; i <= n ; i ++ ){
for(int j = 1 ; j <= m ; j ++ ){
//包含ai不包含aj --和-- 不包含ai包含bj 这两种方案之间比较一下最大公共子序列
f[i][j] = Math.max(f[i - 1][j] , f[i][j - 1]);
//最后一种可能就是ai和bj都包含,不一定存在,需要满足ai == bj时候才满足
if(a[i] == b[j])
f[i][j] = Math.max(f[i][j], f[i - 1][j - 1] + 1);
}
}
//最后输出,从定义出发,输出在【1 - ai】和【1 - bj】两个之间的最长公共子序列
System.out.println(f[n][m]);
}
}
5. 最短编辑距离
原题链接
★f[i][j] 所有把a中的前i个字母 变成 b中前j个字母的集合的操作集合
做题总结
- 由于需要用到前面的数据,所以一定用dp
- i j 相等则 在 i - 1 j-1 的基础 +1
- 如果不相等 则按着 所可以操作的步骤 + 1
import java.util.*;
public class Main{
public static void main(String[] args){
Scanner scan = new Scanner(System.in);
int N = 1010;
char[] a = new char[N];
char[] b = new char[N];
int[][] f = new int[N][N];
int n = scan.nextInt();
String A = scan.next();
int m = scan.nextInt();
String B = scan.next();
for(int i = 1 ; i <= n ; i ++ ) {
a[i] = A.charAt(i - 1);
f[i][0] = i; // 处理边界,字符串b是0,a进行n次删除
}
for(int i = 1 ; i <= m ; i ++ ){
b[i] = B.charAt(i - 1);
f[0][i] = i; // 处理边界,字符串a是0,a进行m次增加
}
for(int i = 1 ; i <= n ; i ++ ){
for(int j = 1 ; j <= m ; j ++ ){
// 删除和增加操作
f[i][j] = Math.min(f[i - 1][j] + 1, f[i][j - 1] + 1);
// 最后一个数相同,不用进行修改操作,则不用加1
if(a[i] == b[j]) f[i][j] = Math.min(f[i][j],f[i - 1][j - 1]);
else f[i][j] = Math.min(f[i][j],f[i - 1][j - 1] + 1); // 修改操作
}
}
System.out.println(f[n][m]);
}
}
6. 编辑距离( 和上题差不多 )
原题链接
三、区间dp
for (int len = 1; len <= n; len++) { // 区间长度
for (int i = 1; i + len - 1 <= n; i++) { // 枚举起点
int j = i + len - 1; // 区间终点
if (len == 1) {
dp[i][j] = 初始值
continue;
}
for (int k = i; k < j; k++) { // 枚举分割点,构造状态转移方程
dp[i][j] = min(dp[i][j], dp[i][k] + dp[k + 1][j] + w[i][j]);
}
}
}
作者:shwei
链接:https://www.acwing.com/solution/content/13945/
来源:AcWing
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
1. ☆ 石子合并
- 从i 到 j 合并 最终 一定是 i j 的区间和
但是划分的时候,不一定用哪一段最小值,所以遍历一下区间,也就是这个题的关键
★f[i][j]表示将 i 到 j 合并的最小值
原题链接
原题链接
![]()
import java.util.*;
public class Main{
public static void main(String[] args){
Scanner scan = new Scanner(System.in);
int N = 310;
int[] s = new int[N];
int[][] f = new int[N][N];
int n = scan.nextInt();
for(int i = 1 ; i <= n ; i ++ ) s[i] = scan.nextInt();
for(int i = 1 ; i <= n ; i ++ ) s[i] += s[i - 1]; // 前缀和
//这里是枚举的每种长度,比如n等于4,比如长度3,右边下标不超过n,求f[1-3]和f[2-4]里面的最小值
for(int len = 2 ; len <= n ; len ++ ){
for(int i = 1; i + len - 1 <= n ; i ++ ){
int j = i + len - 1; // 每种长度的j
//因为要枚举的是k里面的最小值,所以赋一个很大的数,
//如果没有赋最大的数,你的f[i][j] 初始值是0,所以最小是永远会被是0,最后输出也会是0
f[i][j] = (int)1e9;
//这里k是从i开始到j-1结束
for(int k = i ; k < j ; k ++ ){
f[i][j] = Math.min(f[i][j],f[i][k] + f[k + 1][j] + (s[j] - s[i - 1]));
}
}
}
System.out.println(f[1][n]);
}
}
四、计数类DP
题解
1. ☆ 整数划分
原题链接
★f[i][j] 表示 背包为j的 前i个物品 的方案数
方案数 = 拿了i的方案数 + 没拿i的方案数
public class Main{
public static final int N = 1010;
public static final int M = (int) (1e9 + 7);
public static void main(String[] args){
Scanner scan = new Scanner(System.in);
int n = scan.nextInt();
int[][] dp = new int[N][N];
dp[0][0] = 1;//一个数都不选是一种方案
for(int i=1; i<=n; i++){
for(int j=0; j<=n; j++){
for(int k=0; j - k * i >= 0; k++){
dp[i][j] += dp[i - 1][j - k * i];
dp[i][j] %= M;
}
}
}
System.out.println(dp[n][n]);
}
}
五、数位统计dp
★1. 计数问题
原题链接
计数问题—超短写法
dp方法
# include 六、状态压缩DP
1. 蒙德里安的梦想
★f[i][j] 表示已经将前 i -1 列摆好,且从第i−1列,伸出到第 i 列的状态是 j 的所有方案
蒙德里安的梦想
import java.util.*;
public class Main{
public static void main(String[] args){
Scanner scan = new Scanner(System.in);
int N = 12,M = 1 << N;
long[][] f = new long[N][M];
int[][] state = new int[M][M];
boolean[] st = new boolean[M];
while(true){
int n = scan.nextInt();
int m = scan.nextInt();
if(n == 0 && m == 0){ // 如果n跟m同时为0结束循环
break;
}
for(int i = 0 ; i < 1 << n ; i ++ ){
int cnt = 0; // 表示的是当前前面0的个数
boolean flag = true;//表示合法
for(int j = 0 ; j < n ; j ++ ){ // 从上到下判断有多少个0
//判断现在这一位是不是1
if((i >> j & 1) == 1){
//如果是1,判断一下1前面的0的个数是不是偶数,奇数就结束
if((cnt & 1) == 1){ // 判断一个数是不是奇数,&1等于1就是奇数,反之就是偶数
flag = false;
break;
}
cnt = 0;
}else cnt ++ ; // 如果当前不是1,0的个数+1
}
//最后还需要判断一下最后一层0的个数是不是奇数
if((cnt & 1) == 1) flag = false;
st[i] = flag; // 最后将这一种状态存入st数组,表示true合法或者false非合法
}
//这是i-1 到 i列的方块
for(int i = 0 ; i < 1 << n ; i ++ ){
Arrays.fill(state[i],0); // 将所有的状态清零,因为多组数据,防止上一组数据的影响
//这是i-2到i-1列的方块
for(int j = 0 ; j < 1 << n ; j ++ ){
if((i & j) == 0 && st[i | j] ){ // 满足这两个条件的方案合法
//1、i跟j没有相交,2、i-1列的空格数是不是偶数
state[i][j] = 1; // 表示这种方案是合法的,用1表示,0表示不合法
}
}
}
for(int i = 0 ; i < N ; i ++ )
Arrays.fill(f[i],0); // 因为有多组数据,防止上一组数据的干扰,所以清零
f[0][0] = 1; // 什么都没有时候,空着表示一种方案
//最后的dp部分
//为什么从1开始呢,因为从0开始的话,我们定义的f[m][j]就是前i - 1列已经摆好
//如果是0开始,就会从-1个开始摆好,因为我们没有-1列,所以从1开始
for(int i = 1 ; i <= m ; i ++ ){
//枚举i - 1 到 i的所有方案
for(int j = 0 ; j < 1 << n ; j ++ ){
//枚举i - 2 到 i - 1 的所有方案
for(int k = 0 ; k < 1 << n ; k ++ ){
//现在的方案等于前面每种k方案的总和
if(state[j][k] == 1) f[i][j] += f[i - 1][k];
}
}
}
System.out.println(f[m][0]);
}
}
}
2. 最短Hamilton路径
最短Hamilton路径
★f[i][j] 所有从0走到j,所用的点是i的状态的所有路径.
import java.util.*;
public class Main{
public static void main(String[] args){
Scanner scan = new Scanner(System.in);
int N = 20,M = 1 << N;
int[][] f = new int[M][N];//当前的状态是i,然后走到了点j上面
int[][] w = new int[N][N];
int n = scan.nextInt();
for(int i = 0 ; i < n ; i ++ )
for(int j = 0 ; j < n ; j ++ )
w[i][j] = scan.nextInt(); // 输入每一步的权重
for(int i = 0 ; i < 1 << n ; i ++ )
Arrays.fill(f[i],0x3f3f3f); //除了第一个点,其他点初始化成正无穷
f[1][0] = 0;
//首先枚举一下所有的状态
for(int state = 0 ; state < 1 << n ; state ++ ){
//一共有多少步
for(int j = 0 ; j < n ; j ++ ){
// 表示能够走到j,才能进行下一步
if((state >> j & 1) == 1){
//我们用倒数第二步来化整为零
for(int k = 0 ; k < n ; k ++ ){
//首先减掉最后一个点剩下的路径中要能够走到k才能够进行状态计算
if((state - (1 << j) >> k & 1) == 1){
//0 - k - j的途径 f[state - (1 << j)][k] + w[k][j]
f[state][j] = Math.min(f[state][j],f[state - (1 << j)][k] + w[k][j]);
}
}
}
}
}
//最后输出从定义出发,不难想到,f[state][j],state表示的是二进制的全0表示都走过,j表示从0走到n-1
System.out.println(f[(1 << n) - 1][n - 1]);
}
}
七、树形DP
1. ☆ 没有上司的舞会
★f[i][0]所有以u为根的子树中选择,并且不选这个点的方案
★f[i][1]所有以u为根的子树中选择,选这个点的方案
没有上司的舞会
import java.util.*;
public class Main{
static int N = 6010,n,idx;
static int[] happy = new int[N];//每一个职员的快乐指数
static int[][] f = new int[N][2];
static int[] h = new int[N],e = new int[N],ne = new int[N];
static boolean[] st = new boolean[N];//存有负节点的
//领接表
public static void add(int a,int b){
e[idx] = b;
ne[idx] = h[a];
h[a] = idx ++;
}
public static void dfs(int u){
//最坏程度就是那个点不选,就是快乐指数为0
//f[u][0] = 0;
f[u][1] = happy[u];//如果这个点是选的所有,需要加上这个点的快乐指数
for(int i = h[u]; i != -1 ; i = ne[i]){
int j = e[i];
dfs(j);
f[u][0] += Math.max(f[j][0],f[j][1]);//如果这个根节点不选,就等于他的所有根节点选与不选的最大值之和
f[u][1] += f[j][0]; //如果这个根节点选,就等于他的所有根节点不选的和
}
}
public static void main(String[] args){
Scanner scan = new Scanner(System.in);
n = scan.nextInt();
for(int i = 1 ; i <= n ; i ++ ) happy[i] = scan.nextInt();
Arrays.fill(h,-1);
for(int i = 0 ; i < n - 1 ; i ++ ){
int a = scan.nextInt();
int b = scan.nextInt();
add(b,a);//因为b是a的直系上司,所以需要b->a
st[a] = true;//下司就是负节点
}
int root = 1;
while(st[root]) root ++ ; //寻找根节点
dfs(root);
//最后输出的是选根节点跟不选根节点两种方案的最大值
System.out.println(Math.max(f[root][0],f[root][1]));
}
}
八、记忆化搜索
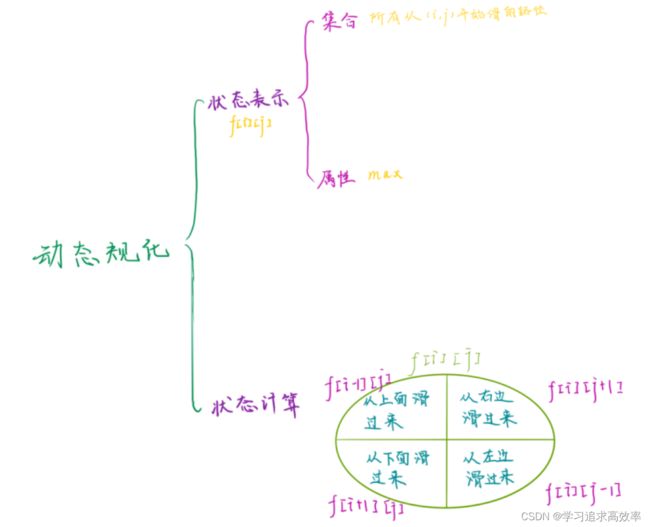
1. 滑雪
★f[i][j] 以(i,j)开始的路径最大值
import java.util.Arrays;
import java.util.Scanner;
public class Main {
static int N = 310;
static int n,m;
static int[][] h = new int[N][N];
static int[][] f = new int[N][N];
static int[] dx = new int[] {0,-1,0,1};
static int[] dy = new int[] {-1,0,1,0};
static int dfs(int x,int y)
{
if(f[x][y] != -1) return f[x][y];
f[x][y] = 1;
for(int i = 0;i < 4;i ++)
{
int a = x + dx[i];
int b = y + dy[i];
if(a < 0 || a >= n || b < 0 || b >= m) continue;
if(h[x][y] > h[a][b]) f[x][y] = Math.max(f[x][y], dfs(a,b) + 1);
}
return f[x][y];
}
public static void main(String[] args) {
Scanner scan = new Scanner(System.in);
n = scan.nextInt();
m = scan.nextInt();
for(int i = 0;i < n;i ++)
{
for(int j = 0;j < m;j ++)
h[i][j] = scan.nextInt();
}
for(int i = 0;i < n;i ++) Arrays.fill(f[i], -1);
int res = 0;
for(int i = 0;i < n;i ++)
{
for(int j = 0;j < m;j ++)
{
res = Math.max(res, dfs(i,j));
}
}
System.out.println(res);
}
}