acwing算法基础课笔记
第一章
基础算法:
一、快速排序:
1.确定区间中的某一点,如a[l],a[r],a[(l+r)/2]等等,
2.将数组分为左右两边,左边全为比分界点小的数,右边全为比分界点大的数,
代码实现:
void quick_sort(int q[],int l,int r)
{
if(l>=r) return 0;//meiyoushu
int i=l-1,j=r+1;
int x=q[l];
while(ix);
if (i y总代码:
上图29行:改为;,31行l,r改为0和n-1,33行将取地址符&去掉。
3.然后分别对左右两边进行递归排序。
tips:
*若选取的为q[l],则底下两个递归为l,j和j+1,r;
为q[r]则为l,i-1和i,r;是互相对称的。
*选q[l],不能用i,只能用j,反之也是一样,,因为这会导致死循环。
较为建议选取q[(l+r)/2];
*(l+r)/2也可以写为(l+r)>>1,即除二取整。
*当输入数据较多时,选择较快的读取方式,在c++中我们选择scanf来进行快速读取。
二、归并排序
1.找分界点
2.递归排序左右两边,将数组分成左右两个有序的数组
3.归并,将两个数组合并成一个有序的数组,通过比较大小插入到一个新的数组中去。
代码实现:
void merge_sort(int q[],int l,int r)
{
if(l>=r) return;
int mid=(l+r)>>1,i=l,j=mid+1;
merge_sort(q,l,mid);
merge_sort(q,mid+1,r);
int k=0;
while(i<=mid && j<=r)
{
if (q[i]<=q[j]) temp[k++]=q[i++];
else temp[k++]=q[j++];
}
while(i<=mid) temp[k++]=q[i++];
while(j<=r) temp[k++]=q[j++];
for(i=l,j=0;i<=r;i++,j++) q[i]=temp[j];
}tips:
快排,归并,与sort速度差不多;
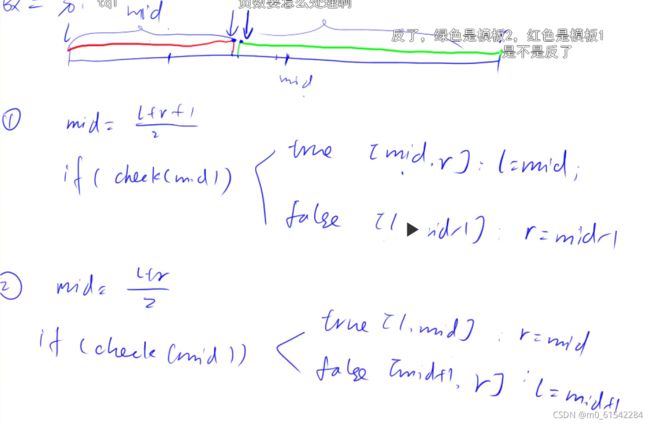
三、二分法查找边界
二分的实质是寻找边界,使用二分法一定能找到边界,至于边界是否与题意有关是否满足不在考虑之内。
因为整数除以是向下取整的,并且边界问题考虑在内,所以我们在使用时需要注意加一减一问题。做题时通过画图思考mid值是否满足要求来确定加一减一。
代码实现:
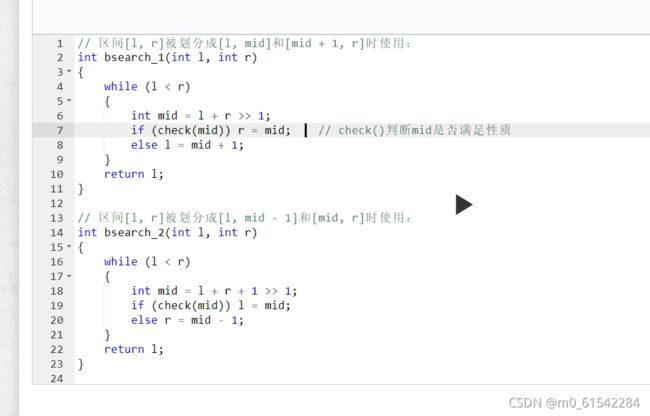
int bsearch1(int l,int r)//找右半边情况
{
while(l>1;
if(check(mid)) r=mid;
else l=mid+1;
}
return l;//r 也行
}
int bsearch2(int l,int r)//找左半边情况
{
while(l>1;
if(check(mid)) l=mid;
else r=mid-1;
}
return l;
} y总代码:
tips:
*若减一则应该在mid计算时加一,否则可能会出现死循环。
*做题时建议直接写mid=l+r>>1;再根据后面判断是否加1;
浮点数二分:不用考虑边界问题,浮点数除以没有取整问题。直接取mid就好,终止条件可为区间长度小于1e-6等;
经验:若结果取四位小数,则为1e-6,若五位小数,则为1e-7;大二即可较精确。
eg:求平方根问题:(判断条件也可不写区间长度,直接暴力重复100次也可)
四、高精度算法
高精度计算大数A和B,A的位数一般小于1e6,而计算A*a时,a的数值一般小于1e9.
对于A+B,我们通过字符串形式读入大数据,在进行逆序存入到vector容器中,因为进位时需要往前加1,所以逆序存入是最好的方式。
代码:
#include
#include
using namespace std;
const int N=1e6+10;//稍大
vector add(vector &A,vector &B)
{
vector C;
int t=0;
for(int i=0;i0) C.push_back(1);//最终有个进位
return C;
}
int main()
{
string a,b;
vector A,B;
cin>>a>>b;
for(int i=a.size()-1;i>=0;i--) A.push_back(a[i]-'0');
for(int i=b.size()-1;i>=0;i--) B.push_back(b[i]-'0');
vector C;
C=add(A,B);
for(int i=C.size()-1;i>=0;i--) cout< 对于A-B,只需要判断哪个大,用大减小就好,需要注意的事项有前导0问题。
代码:
#include
#include
using namespace std;
const int N=1e6+10;//稍大
bool cmp(vector &A,vector &B)
{
if(A.size()!=B.size()) return A.size()>B.size();
else
{
for(int i=A.size()-1;i>=0;i--)//从最高位开始比,出现不同选大的
{
if(A[i]!=B[i]) return A[i]>B[i];
}
}
return true;
}
vector C;
vector sub(vector &A,vector &B)
{
for(int i=0,t=0;i1 && C.back()==0) C.pop_back();//去除前导0
return C;
}
int main()
{
string a,b;
vector A,B;
cin>>a>>b;
for(int i=a.size()-1;i>=0;i--) A.push_back(a[i]-'0');
for(int i=b.size()-1;i>=0;i--) B.push_back(b[i]-'0');
if(cmp(A,B))
{
C=sub(A,B);
for(int i=C.size()-1;i>=0;i--) cout<=0;i--) cout< 高精度乘法
对于小数a,我们将大数的每一位都与a相乘,然后像加法那样记录进位,需要注意的事,乘法也有前导0的问题
代码:
#include
#include
using namespace std;
vector C;
vector mul(vector &A,int b)
{
int t=0;
for(int i=0;i0;i++)
{
if(i1 && C.back()==0) C.pop_back();
return C;
}
int main()
{
string a;
int b;
cin>>a>>b;
vector A;
for(int i=a.size()-1;i>=0;i--) A.push_back(a[i]-'0');
C=mul(A,b);
for(int i=C.size()-1;i>=0;i--) cout< 高精度除法
对于除法,我们将大数从高位开始,每位都对除数相除,记录,取余,存到进位中,给下一位使用,下一位乘以10在加上本身,除以除数,取余,存入,不断重复。因为是从高位开始除并将结果存入c中的,所以C的第一位就应该是输出的第一位,可以使用新的输出代码,或是使用algorithm里的reverse函数,注意除法也有前导0
代码:
#include
#include
#include
using namespace std;
vector C;
vector div(vector &A,int b,int &r)
{
for(int i=A.size()-1;i>=0;i--)
{
r=r*10+A[i];
C.push_back(r/b);
r=r%b;
}
reverse(C.begin(),C.end());
while(C.size()>1 && C.back()==0) C.pop_back();
return C;
}
int main()
{
string a;
int b;
cin>>a>>b;
vector A;
for(int i=a.size()-1;i>=0;i--) A.push_back(a[i]-'0');
int r;
C=div(A,b,r);
for(int i=C.size()-1;i>=0;i--) cout< 二、前缀和
对于一个数组a1,a2,a3...an;
前缀和s[i]表示a1+a2+..+ai;
1.如何求si?
规定s[0]=0;s[i]=s[i-1]+ai;
2.s[i]的作用有哪些?
我们可以求出数组中任意一段区间的和
如[l,r]
sum=s[r]-s[l-1];
#include
using namespace std;
const int N=100010;
int a[N],s[N];
int main()
{
int n,m;
cin>>n>>m;
s[0]=0;
for(int i=1;i<=n;i++)
{
cin>>a[i];
s[i]=s[i-1]+a[i];
}
while(m--)
{
int l,r;
cin>>l>>r;
cout< 对于数据较大时,cin没有scanf快,我们可以使用
ios::sync_with_stdio(false);
来提高cin速度,缺点是不能在使用scanf了;
二维前缀和,sij表示以元素aij为起始点,所有它左上角元素的和
sij怎么存,s[i][j]=s[i-1][j]+s[i][j-1]-s[i-1][j-1]+a[i][j];
里面多加了一遍s[i-1][j-1]所以要减去,
而计算x2,y2到x1,y1之间的元素和
sum=s[x2][y2]-s[x2][y1-1]-s[x1-1][y2]+s[x1-1][y1-1];
跟1有关就减一,然后有一块多减了一次,加回来就好了;
代码:
#include
using namespace std;
const int N=1010;
int a[N][N],s[N][N];
int main()
{
int n,m,q,i,j;
scanf("%d%d%d",&n,&m,&q);
for(i=1;i<=n;i++)
{
for(j=1;j<=m;j++)
{
scanf("%d",&a[i][j]);
}
}
for(i=1;i<=n;i++)
{
for(j=1;j<=m;j++)
{
s[i][j]=s[i-1][j]+s[i][j-1]-s[i-1][j-1]+a[i][j];
}
}
while(q--)
{
int x1,y1,x2,y2;
scanf("%d%d%d%d",&x1,&y1,&x2,&y2);
printf("%d\n",s[x2][y2]-s[x2][y1-1]-s[x1-1][y2]+s[x1-1][y1-1]);
}
return 0;
} 三、差分
一维差分构造两个数组,其中b1=a1,b2=a2-a1;...bn=an-an-1;
这样b数组的和就是ai,即ai=b1+b2+...+bi;
a就是b的前缀和,反过来b就是a的差分
用处:已知b差分数组,可以通过求b的前缀和来求出a数组,如果我们要让a数组的[l,r]之间元素全都+c,只需要将b[l]+=c,这时候a[l]之后所有数都会+c,我们再让b[r+1]-=c;这样人之后的a数组就不会有变化。
对于构造差分数组,我们可以看成读入a[i]时,进行了在i到i区间上加了一个a[i]大小的数,这样b数组就自然而然的出现了;
#include
using namespace std;
const int N=100010;
int a[N],b[N];
void insert(int l,int r,int c)
{
b[l]+=c;
b[r+1]-=c;
}
int main()
{
int n,m,i;
scanf("%d%d",&n,&m);
for(i=1;i<=n;i++) scanf("%d",&a[i]);
for(i=1;i<=n;i++) insert(i,i,a[i]);
while(m--)
{
int l,r,c;
scanf("%d%d%d",&l,&r,&c);
insert(l,r,c);
}
for(i=1;i<=n;i++) b[i]+=b[i-1];
for(i=1;i 二维差分,想要在一块a的子矩阵x1,y1到x2,y2内加上c,我们先在b的x1,y1加上c,这时它的右下角所以a的元素都会加c,我们让b[x1][y2+1]-=c,b[x2+1][y1]-=c,b[x2+1][y2+1]+=c(减了两次)就可以实现了,这完全是前缀和的求反。
代码:
#include
using namespace std;
const int N=1010;
int a[N][N],b[N][N];
void insert(int x1,int y1,int x2,int y2,int c)
{
b[x1][y1]+=c;
b[x1][y2+1]-=c;
b[x2+1][y1]-=c;
b[x2+1][y2+1]+=c;
}
int main()
{
int n,m,q;
scanf("%d%d%d",&n,&m,&q);
int i,j;
for(i=1;i<=n;i++)
{
for(j=1;j<=m;j++)
{
scanf("%d",&a[i][j]);
}
}
for(i=1;i<=n;i++)
{
for(j=1;j<=m;j++)
{
insert(i,j,i,j,a[i][j]);
}
}
while(q--)
{
int x1,y1,x2,y2,c;
scanf("%d%d%d%d%d",&x1,&y1,&x2,&y2,&c);
insert(x1,y1,x2,y2,c);
}
for(i=1;i<=n;i++)
{
for(j=1;j<=m;j++)
{
b[i][j]=b[i][j]+b[i-1][j]+b[i][j-1]-b[i-1][j-1];
}
}
for(i=1;i<=n;i++)
{
for(j=1;j<=m;j++)
{
cout< 三,基础算法三
双指针算法
用处:将原本为o(n方)复杂度的算法优化为o(n)复杂度算法,中间思路较为重要;
eg:最长连续不重复子序列
求一段序列中最长的不重复子列
我们将i在前走,j在后面等,如果ij之间存在重复数,则j++,因为是从0开始的,所以重复的肯定是最新的i,一直j++,直到 ij内无重复为止。
#include
using namespace std;
const int N=1e5+10;
int a[N];
int s[N];
int main()
{
int n,i,j;
cin>>n;
for(i=0;i>a[i];
int res=0;
for(i=0,j=0;i=j&&s[a[i]]>1)
{
s[a[j]]--;
j++;
}
res=max(res,i-j+1);
}
cout< 位运算:取二进制数的第k位,将第k位数移到最后一位,代码为n>>k,
查看数x的最后一位 :x&1;
即求n的二进制第k位:n>>k&1;
求x的最后一位1,代码为:x&-x;
举例:求x中1的位数,可以用
while(x)
{ x-=lowbit(x);
res++;
}来实现
离散化:将一连串(最大为1e5个数)大小值小于1e9的有序数,用0到n表示。
代码:(这个二分找到的是第一个大于等于x的数)
vector alls;
sort(alls.begin(),alls.end());
alls.erase(unique(alls.begin(),alls.end()),alls.end());//unique会将重复元素排到容器尾部,erase则是删去这些数。
int find(int x)
{
int l=0,r=alls.size()-1;
while(l>1;
if(alls[mid]>=x) r=mid;
else l=mid+1;
}
return r+1;//+1可以不加,加了的话就是1到n,不加就是0到n-1;
} 离散化特点:数的范围区间跨度等非常大,但是非常的稀疏,非常离散
区间合并,将所有区间的左端点进行排序,然后每次维护一个区间,观察这个区间是否需要扩容合并,不需要则维护下一个区间。用pair来记录左右端点,vector来存。
#include
#include
#include
using namespace std;
const int N=100010;
typedef pair PII;
vector segs;
void merge(vector &segs)
{
vector res;
int st=-2e9,ed=-2e9;
sort(segs.begin(),segs.end());
for(auto seg:segs)
{
if(ed< seg.first)
{
if(st!=-2e9) res.push_back({st,ed});
st=seg.first;
ed=seg.second;
}
else ed=max(ed,seg.second);
}
if(st!=-2e9) res.push_back({st,ed});
segs=res;
}
int main()
{
int n,i,j;
cin>>n;
for(i=0;i>l>>r;
segs.push_back({l,r});
}
merge(segs);
cout<