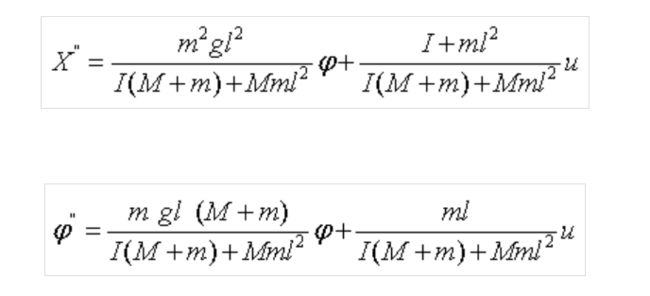基于LQR算法的一阶倒立摆控制

1. 一阶倒立摆建模

2. 数学模型

倒立摆的受力分析网上有很多，这里就不再叙述。直接放线性化后的方程：

F = (M+m)x″-mLφ″
(I+mL²)φ″= mLx″+ mgLφ

（F为外力，x为物块位移，M，m为物块和摆杆的质量，φ为摆杆相对竖直向上方向的角度）

然后建立状态控制方程：

得到状态矩阵为：

3. python代码

# lqr.py

#!/usr/bin/env python3
# -*- coding: utf-8 -*-

import control
import numpy as np

M = 1.0      # 小车质量
m = 1.0      # 摆杆质量
g = 9.8      # 重力加速度
L = 2.0      # 摆杆长度

I = 1.0 / 3.0 * m * (L*L)      # 均质摆杆转动惯量

print("I is: ", I)

A_23 = -(m*m) * (L*L) * g / (I * (M + m) + M * m * (L*L))
A_43 = (M + m) * m * g * L / (I * (M + m) + M * m * (L*L))

print("A_23 is: ", A_23)
print("A_43 is: ", A_43)

B_2 = (I + m * (L*L)) / (I * (M + m) + M * m * (L*L))
B_4 = -m * L / (I * (M + m) + M * m * (L*L))

print("B_2 is: ", B_2)
print("B_4 is: ", B_4)

A = np.array([[0, 1, 0,    0], 
              [0, 0, A_23, 0], 
              [0, 0, 0,    1], 
              [0, 0, A_43, 0]])

# B = np.array([[0], [B_2], [0], [B_4]])
_B = np.array([0, B_2, 0, B_4])
B = _B.reshape(_B.shape[0],1)

Q = np.array([[100, 0, 0,   0],
              [0,   1, 0,   0],
              [0,   0, 100, 0],
              [0,   0, 0,   1]])

R = 10

K = control.lqr(A, B, Q, R)

print("K is: ", K)

执行结果：

$ ./lqr.py 
I is:  1.3333333333333333
A_23 is:  -5.880000000000001
A_43 is:  5.880000000000001
B_2 is:  0.8
B_4 is:  -0.30000000000000004
K is:  (array([[ -3.16227766,  -6.43571648, -83.62359638, -39.56913008]]), array([[  203.5152246 ,   206.59223321,  1251.28576097,   656.32187724],
       [  206.59223321,   292.76442691,  1890.23514953,   995.22902118],
       [ 1251.28576097,  1890.23514953, 15580.3357274 ,  7828.080278  ],
       [  656.32187724,   995.22902118,  7828.080278  ,  3972.91505928]]), array([-2.38935921+0.27045155j, -2.38935921-0.27045155j,
       -0.97172371+0.81464125j, -0.97172371-0.81464125j]))

---

参考：
一阶倒立摆simscape建模