基于minist数据集用VAE训练生成图片(VAE基础入门学习)
文章目录
- 参考的代码
- VAE介绍
- 代码实现与解读
-
- 代码块
- 累计损失函数的变化
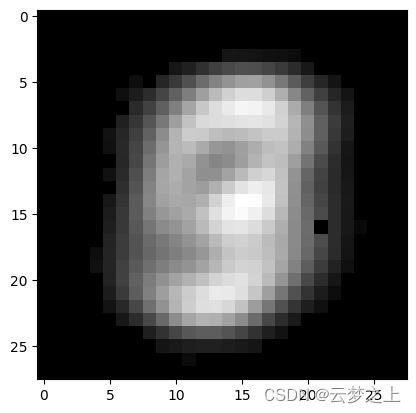
- 迭代100次后生成的图像
参考的代码
复现的代码
VAE介绍
VAE是变分自编码器(Variational Auto-Encoder)的缩写。它是一种深度生成模型,由 Kingma 等人于 2014 年提出的基于变分贝叶斯(Variational Bayes,VB)推断的生成式网络结构1. VAE 模型有两部分,分别是一个编码器和一个解码器,常用于 AI 图像生成。
训练模型的网络的结构
#所以整个VAE的图像形状的变化流程就是,
#输入:batchsize*28*28
#编码器:
#28*28 - 100
#100 - 100
#_sample_latent
#100 - 8
#解码器:
#8 -100
#100 - 28*28
损失函数loss包括两部分:重构误差和KL散度
重构误差
重构误差(reconstruction error)计算得出的,它反映了解码器解码得到的向量与输入向量之间的差异.一般用均方差来计算
KL散度
KL 散度项用于衡量潜在空间中的分布与标准正态分布之间的差异
VAE的作用
通过神经网络学习到分布的转换过程,那么可以实现图像的压缩,只记录中间过程,然后通过中间过程根据模型生成重建后的图像VAE的作用是生成新的图像,而不是还原原图像。
通过学习数据的潜在分布,VAE可以从该分布中生成与训练数据相似但不完全相同的新样本。
代码实现与解读
代码块
import torch
import torch.nn.functional as F
from torch.autograd import Variable
import torchvision
from torchvision import transforms
import torch.utils.data as Data
import torch.optim as optim
from torch import nn
import numpy as np
import matplotlib.pyplot as plt
import os
import torchsummary
from torchsummary import summary
#summary(your_model, input_size=(channels, H, W))
os.environ["CUDA_VISIBLE_DEVICES"] = '3'
class Normal(object):
def __init__(self, mu, sigma, log_sigma, v=None, r=None):
self.mu = mu
self.sigma = sigma
self.logsigma = log_sigma
dim = mu.get_shape()
if v is None:
v = torch.FloatTensor(*dim) # create a tensor
if r is None:
r = torch.FloatTensor(*dim)
self.v = v
self.r = r
class Encoder(torch.nn.Module):
def __init__(self, D_in, H, D_out): # input_dim, hidden_dim, hidden_dim
super().__init__()
self.liner1 = torch.nn.Linear(D_in, H) # dimension(D_in, H)
self.liner2 = torch.nn.Linear(H, D_out)
def forward(self, x):
x = F.relu(self.liner1(x))
return F.relu(self.liner2(x))
class Decoder(torch.nn.Module):
def __init__(self, D_in, H, D_out): # latent_dim, hidden_dim, input_dim
super().__init__()
self.liner1 = torch.nn.Linear(D_in, H)
self.liner2 = torch.nn.Linear(H, D_out)
def forward(self, x):
x = F.relu(self.liner1(x))
return F.relu(self.liner2(x))
class VAE(torch.nn.Module):
def __init__(self, encoder, decoder, latent_dim, hidden_dim): # 定义构造方法
super().__init__() #调用父类方法
self.encoder = encoder
self.decoder = decoder
self._enc_mu = torch.nn.Linear(hidden_dim, latent_dim) # 神经网络线性模块
self._enc_log_sigma = torch.nn.Linear(hidden_dim, latent_dim)
#这里对μ和σ的学习,只是利用神经网络得到两个向量,然后加入的正太分布的大小也和μ和σ的维度是一样的
#sample——latent加在了encoder和decoder之间,进行一个维度的转化,以及参数的重构,增加我们模型的参数,让我们的模型更有泛化能力
def _sample_latent(self, h_enc):
"""
:param h_enc:
:return: the latent normal sample z ~ N(mu, sigma^2)
"""
mu = self._enc_mu(h_enc)
log_sigma = self._enc_log_sigma(h_enc)
sigma = torch.exp(log_sigma) # y = e^x
std_z = torch.from_numpy(np.random.normal(0, 1, size=sigma.size())).float() # 讲numpy转成tensor
self.z_mean = mu
self.z_sigma = sigma
return mu + sigma * Variable(std_z, requires_grad=False) # Reparametization trick
def forward(self, state):
#前向传播,将图像数据转化为size为 batch_size*8 的形式
h_enc = self.encoder(state)
#然后利用重参数化技巧,将encoder的结果转化为decoder可以处理的结果
z = self._sample_latent(h_enc)
#最后用decoder对图像进行还原
return self.decoder(z)
def latent_loss(z_mean, z_stddev):
mean_sq = z_mean * z_mean
stddev_sq = z_stddev * z_stddev
return 0.5 * torch.mean(mean_sq + stddev_sq - torch.log(stddev_sq) - 1)
latent_dim = 8
hidden_dim = 100
input_dim = 28 * 28
batch_size = 32
transform = transforms.Compose([transforms.ToTensor()]) # pytorch 的一个图形库
mnist = torchvision.datasets.MNIST('./', download=True, transform=transform)
dataloader = Data.DataLoader(mnist, batch_size=batch_size, shuffle=True, num_workers=2) # 用来把训练数据分成多个小组,此函数每次抛出一组数据。直至把所有的数据都抛出
encoder = Encoder(input_dim, hidden_dim, hidden_dim)
decoder = Decoder(latent_dim, hidden_dim, input_dim)
vae = VAE(encoder, decoder, latent_dim, hidden_dim)
#所以整个VAE的图像形状的变化流程就是,
#输入:batchsize*28*28
#编码器:
#28*28 - 100
#100 - 100
#_sample_latent
#100 - 8
#解码器:
#8 -100
#100 - 28*28
criterion = nn.MSELoss() # 均方损失函数: loss(x_i,y_i) = (x_i, y_i)^2
optimizer = optim.Adam(vae.parameters(), lr=0.0001) # 为了使用torch.optim,需先构造一个优化器对象Optimizer,用来保存当前的状态,并能够根据计算得到的梯度来更新参数,lr学习率
# Adam 自适应 SGD随机梯度下降
l = 0
for epoch in range(100):
for i, data in enumerate(dataloader, 0):
inputs, classes = data
#Variable的作用是将 tensor 转换为可以进行自动求导的对象
inputs, classes = Variable(inputs.resize_(batch_size, input_dim)), Variable(classes)
optimizer.zero_grad() # 梯度置0
#vae返回的是解码器生成的图像
dec = vae(inputs)
#计算在sample过程中的潜在损失
la_loss = latent_loss(vae.z_mean, vae.z_sigma)
loss = criterion(dec, inputs) + la_loss
loss.backward() # 反向传播,计算当前梯度;
optimizer.step() # 根据梯度更新网络参数
l += loss.item()
#这里是损失函数的累加,所以损失的值是不断增大
print(epoch, l)
#最后我们得到的VAE能给定一个图像,然后其对图像进行压缩,然后解码为另一个图像(实现图像的转换,风格的变化)
#VAE的作用是生成新的图像,而不是还原原图像。通过学习数据的潜在分布,VAE可以从该分布中生成与训练数据相似但不完全相同的新样本。
plt.imshow(vae(inputs).data[0].numpy().reshape(28, 28), cmap='gray')
plt.show(block=True)
累计损失函数的变化
0 139.16818779706955
1 267.87674168124795
2 395.3811474405229
3 522.4189930967987
4 649.2481354251504
5 775.955449514091
6 902.5857038684189
7 1029.162303648889
8 1155.701839581132
9 1282.207650154829
10 1408.6873084045947
11 1535.1423131600022
12 1661.581350132823
13 1788.0235249735415
14 1914.4417337104678
15 2040.8419712409377
16 2167.2386958152056
17 2293.6268618367612
18 2420.0079036839306
19 2546.382174734026
20 2672.755078855902
21 2799.1218701675534
22 2925.488541547209
23 3051.846152242273
24 3178.199055157602
25 3304.5493181720376
26 3430.8967041336
27 3557.2448443993926
28 3683.589498732239
29 3809.9357734806836
30 3936.2771221250296
31 4062.6171908825636
32 4188.954324498773
33 4315.289867065847
34 4441.629120387137
35 4567.959967684001
36 4694.293099652976
37 4820.619683727622
38 4946.952780801803
39 5073.282864153385
40 5199.609850440174
41 5325.9397988170385
42 5452.265446525067
43 5578.591994319111
44 5704.914690893143
45 5831.23753689602
46 5957.559496037662
47 6083.884328097105
48 6210.208755288273
49 6336.530883956701
50 6462.851982541382
51 6589.169302016497
52 6715.490865979344
53 6841.8104959875345
54 6968.132151730359
55 7094.45059369877
56 7220.767149258405
57 7347.088673260063
58 7473.406335223466
59 7599.724608790129
60 7726.037183042616
61 7852.353367693722
62 7978.6651857718825
63 8104.976332779974
64 8231.28970463574
65 8357.603039838374
66 8483.91544116661
67 8610.230692859739
68 8736.543450322002
69 8862.851587157696
70 8989.160839147866
71 9115.472040515393
72 9241.782772105187
73 9368.089835889637
74 9494.398323338479
75 9620.7102698721
76 9747.017931006849
77 9873.32592940703
78 9999.633243571967
79 10125.944087844342
80 10252.24886193499
81 10378.557406943291
82 10504.867665823549
83 10631.173416335136
84 10757.483445655555
85 10883.788483023643
86 11010.096190895885
87 11136.400267038494
88 11262.704502705485
89 11389.009268335998
90 11515.318977285177
91 11641.624094836414
92 11767.9290404059
93 11894.233354754746
94 12020.536377009004
95 12146.839713525027
96 12273.143506359309
97 12399.446860846132
98 12525.751429088414
99 12652.052845072001