pytorch 深度学习实践 第三讲 梯度下降算法
第三讲 梯度下降算法 gradient Descent
pytorch学习视频——B站视频链接:《PyTorch深度学习实践》完结合集哔哩哔哩bilibili
以下是视频内容的个人笔记,主要是梯度下降算法的理解和简单公式实例,以及两个视频中的小练习源码,如有错误请指出,三扣。
目录
第三讲 梯度下降算法 gradient Descent
梯度下降法gradient Descent
gradient.py 源码
随机梯度下降法
stochastic_gradient.py
学习笔记:
梯度下降法gradient Descent
-
大致原理:
目标函数对参数求偏导——参数沿着此偏导数为负的方向变化(目标损失函数随着参数的变化而减少)——也即目标函数沿梯度下降最快的方向变化。
-
for example:
要求解W在cost最小时的最优解,求损失函数cost对W的一阶偏导数,取偏导数为负的方向
W沿着此方向变化(梯度下降)——> (α 是学习率,即控制下降的快慢)。cost的值可以下降得最快,并且可以到达局部最优解(贪心思想)。
如图所示:
- 局部最优和全局最优
如图所示,局部最优处无法再继续下降到全局最优,因为局部到全局的上升的部分是偏导数为正的方向(图中红色小箭头处),梯度下降法无法到达全局最优。
所以在神经网络训练时有可能会只达到局部最优点,但是实际上神经网络中的损失函数并没有很多局部最优点。
因此,在实际情况中要解决的是鞍点(梯度等于0)问题,如图所示:
此时的W无法再继续迭代下去找到全局最优。
- 梯度下降法实例
对w求偏导,计算w的具体更新过程,如图所示:
-
gradient.py 源码
import matplotlib.pyplot as plt
x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]
w = 1.0
print(w)
# 模型函数 y= w*x
def foward(x):
return x * w
# 全部数据的损失函数总和平均
def cost(xs, ys):
cost = 0
for x, y in zip(xs, ys):
y_pred = foward(x)
cost += (y_pred-y) ** 2
return cost / len(xs)
# 梯度下降
def gradient(xs, ys):
grad = 0
for x, y in zip(xs, ys):
grad += 2 * x * (x * w - y)
return grad / len(xs)
# 训练当达到最优值时,即损失函数梯度grad下降到梯度为0,W的值不再继续迭代
print("Predict(before training)", 4, foward(4))
epoch_list = []
loss_list = []
for epoch in range(100):
loss = cost(x_data, y_data)
grad_val = gradient(x_data, y_data)
# 如果未达到最优,可以修改学习率试试
w -= 0.01 * grad_val
if epoch % 10 == 0:
print("epoch:", epoch, "w=", w, "loss=", loss)
epoch_list.append(epoch)
loss_list.append(loss)
print("Predict(after traning)", 4, foward(4))
plt.plot(epoch_list, loss_list,)
plt.xlabel('epoch')
plt.ylabel('loss')
plt.show()结果:
-
随机梯度下降法
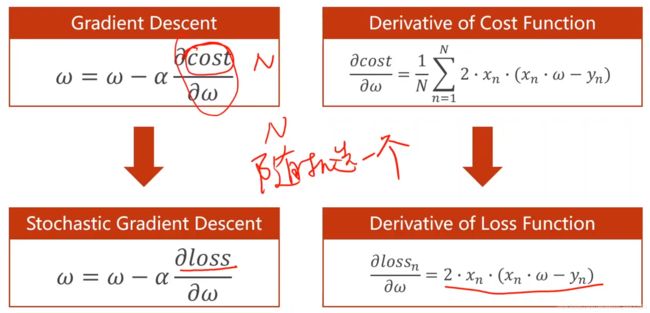
用总的损失函数cost对W求偏导的梯度下降可能会存在上述的鞍点问题,所以将某一个数据的loss损失函数作为梯度下降得方法,由于噪声的存在可能可以有效处理鞍点问题——随机梯度。如图所示:
w根据梯度的下降来更新,如果loss对w求导等于0,也就是梯度为0了,那w就不再继续迭代变化,理论上可以保持最优。
-
stic_gradient.py
import matplotlib.pyplot as plt
x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]
w = 1.0
print(w)
# 模型函数 y= w*x
def foward(x):
return x * w
# 单个数据的损失函数
def loss(x, y):
y_pred = foward(x)
return (y_pred - y) ** 2
# 梯度下降
def gradient(x, y):
grad = 2 * x * (x * w - y)
return grad
# 训练当达到最优值时,即损失函数梯度grad下降到梯度为0,W的值不再继续迭代
print("Predict(before training)", 4, foward(4))
epoch_list = []
loss_list = []
for epoch in range(100):
for x, y in zip(x_data, y_data):
# 不断根据单组数据的梯度下降方向来调整W
grad = gradient(x, y)
w -= 0.05 * grad
print("\tgrad: ", x, y, grad)
l = loss(x, y)
print("epoch:", epoch, "w=", w, "loss=", l)
epoch_list.append(epoch)
loss_list.append(l)
print("Predict(after traning)", 4, foward(4))
plt.plot(epoch_list, loss_list,)
plt.xlabel('epoch')
plt.ylabel('loss')
plt.show()结果:
-
Batch——Mini-Batch
但是如果对每一个样本都计算一次损失,那每个样本的计算都得串行执行,因为每个样本求梯度时使用的w都是上一个样本更新之后的w。如果用总的loss则可以全部数据都并行计算,因为各个样本用的w没有依赖关系,使用的是上一次训练周期的w。所以综上取一个性能和时间都折中的办法——Batch批次训练。每次计算一组batch的梯度然后更新权重
(代码理解请参考注释,以上代码已经在pycharm上经过测试,笔记纯属个人理解,如有错误欢迎路过的大佬指出 嘻嘻嘻。)
——未完待续……