二叉树的遍历总结
二叉树的遍历
二叉树的遍历分为前序遍历、中序遍历、后续遍历和层次遍历,前三种可看作是深度优先遍历,层次遍历可看作广度优先遍历,先介绍前三种。
前、中、后序遍历
前中后的区分主要在于什么时候处理根节点,若是根左右(或叫中左右)根最前遍历则为前序遍历,依次类推,左根右为中序遍历,左右根为后序遍历。
根左右的意思是对于每一个子树,先遍历根节点,再访问左子节点,再访问右子节点,注意是对每一个子树。例如对树:
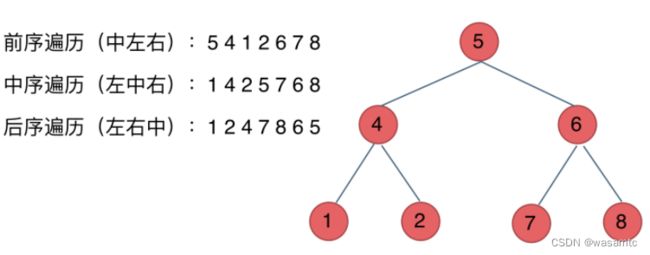
递归写法
这三种遍历来说递归实现是比较好理解的。写递归,主要就三点:
- 要传递的参数
- 递归终止条件
- 递归处理逻辑
例如对于前序遍历:
class Solution {
void traversal(TreeNode* node, vector<int> &result) {
if (node == nullptr)
return;
result.push_back(node->val);
traversal(node->left, result);
traversal(node->right, result);
}
vector<int> preorderTraversal(TreeNode* root) {
vector<int> result;
traversal(root, result);
return result;
}
}
这种递归比较好理解,其他两种遍历方式更改一下顺序就行。
迭代写法
迭代写法又有非统一写法和统一写法,都用栈来实现。
非统一写法
非统一写法中序遍历和其他两种遍历不同,主要前序遍历是边访问边处理,后序遍历可通过前序遍历变形而来,而中序遍历第一次访问节点时并不处理,下一次访问时才处理。
首先看前序遍历
class Solution {
vector<int> preorderTraversal(TreeNode* root) {
vector<int> result;
if (!root)
return result;
stack<int> st;
// 前序遍历这种写法的核心就是直接处理栈顶元素,然后压入其余元素
st.push(root);
while (!st.empty()) {
TreeNode *node = st.top();
st.pop();
// 注意压栈的时候要反着压
result.push_back(node->val);
if (node->right) st.push_back(node->right);
if (node->left) st.push_back(node->left);
}
return result;
}
}
因为前序遍历是根左右,后序遍历是左右根,所以可以把前序遍历的顺序变为根右左,然后把结果reverse了,代码如下:
class Solution {
vector<int> preorderTraversal(TreeNode* root) {
vector<int> result;
if (!root)
return result;
stack<int> st;
// 前序遍历这种写法的核心就是直接处理栈顶元素,然后压入其余元素
st.push(root);
while (!st.empty()) {
TreeNode *node = st.top();
st.pop();
// 注意压栈的时候要反着压
result.push_back(node->val);
if (node->left) st.push_back(node->left);
if (node->right) st.push_back(node->right);
}
reverse.(result.begin(), result,end());
return result;
}
}
中序遍历就有一点点麻烦了,因为中序遍历是一直访问左子节点直到没有节点可访问了再处理上一个左子节点,那么如何判断没有节点访问了呢,很简单,只要栈顶元素为nullptr就行,没有节点访问了就弹出栈顶元素,再压入右子节点,因为根节点之前压入过了,等到右子节点为空了就可以处理根节点了。代码如下:
class Solution {
vector<int> preorderTraversal(TreeNode* root) {
vector<int> result;
stack<int> st;
TreeNode *cur;
while (cur != nullptr || !stack.empty()) {
if (cur != nullptr) {
// 一直压入左子节点知道左子节点为空
stack.push(cur);
cur = cur->left;
}
else {
// 处理栈顶元素
cur = stack.top():
stack.pop();
result.push_back(cur->val);
cur = cur->right;
}
}
return result;
}
}
非统一写法主要就是模拟,前序遍历就是边访问边处理,中序遍历就是先把左子树深入访问完再处理。
统一写法
我比较喜欢统一写法,统一写法的思想也比较简单,就是第一次访问的时候不处理,下一次访问的时候处理,至于怎么决定什么时候节点下一次访问,就要看压入的顺序了,而要判断是第二次访问是通过第一次访问某一节点的时候在其后面压入一个空节点。
例如中序遍历的代码:
class Solution {
vector<int> preorderTraversal(TreeNode* root) {
vector<int> result;
if (!root)
return result;
stack<int> st;
st.push(root);
while (!st.empty()) {
TreeNode *node = st.top();
if (!node) {
st.pop();
// 这个根据遍历方式不同顺序也不同
if (node->right) st.push(node->right);
st.push(node);
// 压入一个空指针代表当前节点已经访问过了
st.push(nullptr);
if (node->left) st.push(node->left);
}
else {
st.pop();
node = st.top();
st.pop();
result.push_back(node-val);
}
}
return result;
}
}
前序遍历和后序遍历该一下压入的顺序就好了。
差不多二叉树的深入优先遍历就是这样,我觉得使用优先级是递归 > 统一迭代 > 大于非统一迭代。
层次遍历
二叉树的层次遍历比较容易实现,直接用队列即可。队列存储的是当前层的结点。每次取这一层的结点,存入结果中,同时把下一层的结点存入队列。代码如下:
class Solution {
public:
vector<vector<int>> levelOrder(TreeNode* root) {
vector<vector<int>> result;
if (!root)
return result;
queue<TreeNode*> que;
que.push(root);
while (!que.empty()) {
int queSize = que.size();
TreeNode *node;
vector<int> temp;
for (int i = 0; i < queSize; i++) {
node = que.front();
que.pop();
temp.push_back(node->val);
if (node->left) que.push(node->left);
if (node->right) que.push(node->right);
}
result.push_back(temp);
}
return result;
}
};
二叉树的遍历差不多就是这样。
