排序算法实验

欢迎来我的网站交流

（1）排序算法

分别实现归并排序、快速排序和堆排序，输入规模N=16,32,64,128,256，512，…，输入数据随机生成1-10000之间的整数，记录实验结果，做出运行时间与输入规模之间的关系曲线图，说明算法的时间复杂度和空间复杂度，根据曲线图比较3种排序算法的优劣。

排序算法结果：

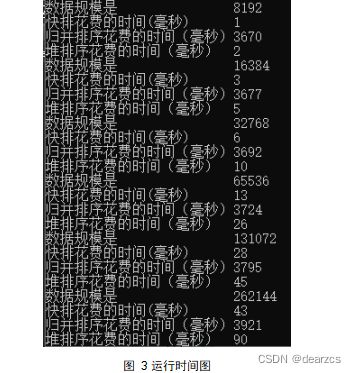
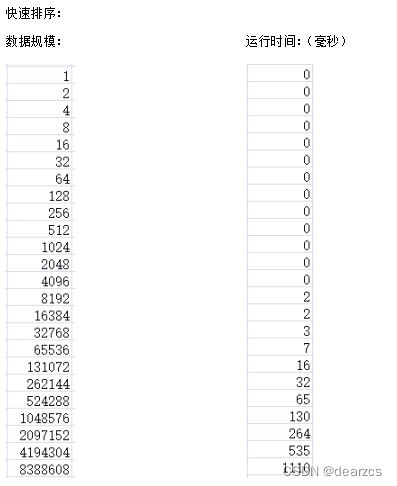
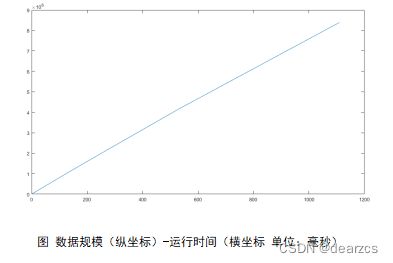
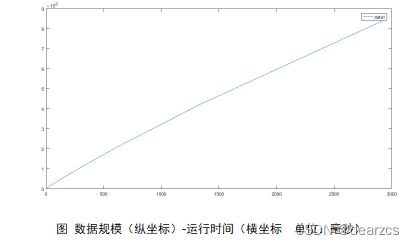
快排运行时间可视化

理论快排时间复杂度计算

最好情况：每趟最终结果是左侧与右侧等长，结合代码可以得出递推式的时间复杂度：   T(n) = 2T(n/2) + 7 + 9n/2  (n > 1)
       T(1) = 1
       满足分治推导式
       a  = 2,b = 2,k = 1.
       推出  T（n） = O(nlog(n)) (以2为底)（此处为大概量级不是精准值）
最坏情况：待排序数据每次划分后都是正序或者逆序，此时需要递归n-1次才能完成排序，每趟需要比较n - i次才能找到i的位置，
因此时间复杂度为：O（n^2）（此处为大概量级不是精准值）

由归纳法可证明：平均时间复杂度为O(nlog(n)) (以2为底)（此处为大概量级不是精准值）
分析实验数据，前面部分较小数据规模时，因为花费时间小于1毫秒未能统计，从统计到的数据以及  数据规模-时间图  
可得到实验结果大致上满足理论。  

理论空间复杂度：
每层循环 定义了三个int类型变量， 循环层数最多n-1层，最少log(n)(以2为底),所以空间开销为 
 3log(n)+n 到 4n - 3 之间，所以快排的空间复杂度为O（n）
的量级

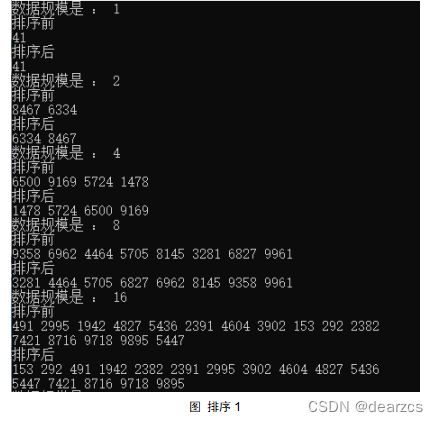
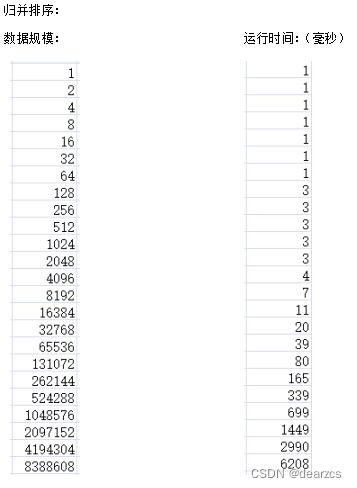
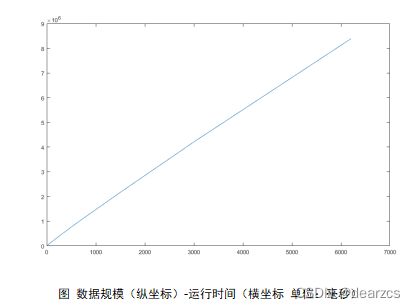
归并排序运行时间可视化

理论归并排序时间复杂度计算

T(n) = 2T(n/2) + 3n + 8  (n > 1)
T(1) =1
       满足分治推导式
        a = 2,b = 2,k = 1.
        T（n） = O(nlog(n)) (以2为底)（此处为量级不是精准值）
分析实验数据，前面部分较小数据规模时，从统计到的数据以及  数据规模-时间图  可得到实验结果大致上满足理论。
理论空间复杂度：
归并排序有 log(n)(以2为底)层， 每层空间开销为n,还有定义变量的空间开销
大致为 4n - 4(将归并排序展开可以得到类似一个满二叉树的结构，每个结点定义变量的空间花费为 4, 总共有 n - 1个结点)，
存储数据花费 n 的空间，所以总共：花费了 nlog(n) + 5n - 4; 大致为O（nlog(n)）的量级 （都是以2为底）

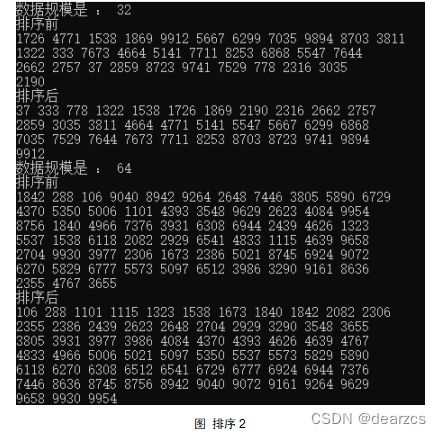
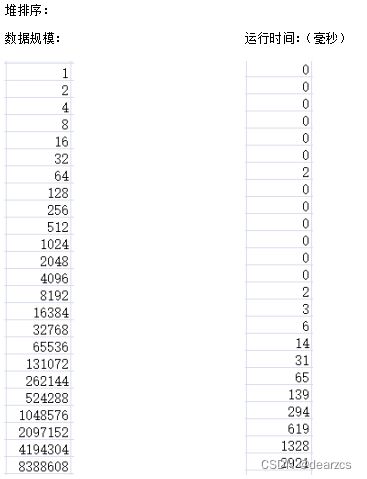
堆排序运行时间可视化

理论堆排序时间复杂度计算：

算法SiftHeap将根节点与左右子树的根结点进行比较，若不满足堆的条件，则将根结点与左右子树根结点的较大者进行交换，
所以，每比较一次，需要调整的完全二叉树的问题规模就减少一半，因此，其时间性能是O（log(n)）以2为底
然后分析HeapSort，第一个for循环大致上会执行 log(n) 次 SiftHeap函数 （以2为底）
第二个for循环调用了 n-1 次SiftHeap函数
所以总和为 (n-1 + log(n))log(n) 大致等于 nlog(n) 的量级
所以堆排序的时间复杂度量级约为 O(nlog(n))
理论空间复杂度：
第一个for 大致是 log(n)(以2为底)
第二个for 大致是 n-1
存储数据花费 n
所以总共是 n + 2(n-1) + 2log(n) = 3n -2 + 2log(n)大致是 O（n）

算法介绍

快排算法描述：

功能：排序
输入：待划分的记录序列data[first]~data[last]
输出：无
      1. 设置划分区间：i = first; j = last;
      2.重复下述过程，直到i> = j;
         2.1 右侧扫描，直到data[j]小于data[i];将data[j]与data[i]交换，i++；
         2.2 左侧扫描，直到data[i]大于data[j];将data[i]与data[j]交换，j--;
      3.对j点左侧进行快速排序；
      4.对j点右侧进行快速排序；

归并排序算法描述：

功能：排序
输入：待划分的记录序列data[first]~data[last]
输出：无
1.将待排序序列{r1,r2,......,rn}划分为两个长度相等的子序列{r1,r2,...,r(n/2)}          
和{r(n/2+1),...,rn}，分别对这两个子序列进行排序，得到两个有序子序列
2.再将这两个有序子序列合并成一个有序序列。

堆排序算法描述：

函数 Sift(k,last)
功能：将一个数组进行堆调整（这里就调整为大根堆）
输入：待调整的记录data[k]~data[last]，且data[k+1]~data[last]满足堆的条件
输出：无
      1.设变量i和j分别指向当前需要调整的结点和要调整的结点的左孩子；
      2.若结点i已是叶子，则算法结束；否则。执行下述操作；
          2.1将j指向结点i的左右孩子中的较大者
          2.2如果data[i]大于data[j],则调整完毕，算法结束
          2.3如果data[i]小于data[j],则将data[i]与data[j]交换；令i=j；j = 2*i+1;

三个排序的数据处理：
为了充分体现三种排序的运行时的时间差异，所以必须保证三种排序处理的原数据得完全一样，所以设置三个空间足够大的数组，数据规模1，2，4，8~~~~~递增，相同数据规模下，使用一个随机函数生成随机数，并赋值给三个数组，也只统计了三种方法排序时花费的时间。

代码

题目1：
#include
#include
#include
#include
#include
using namespace std;
const int N = 1e7 + 10;
struct Counts
{
    long long q,m,h,t;

}counts[N];

int n;
int qt[N];
int ht[N];
int mt[N];
int pt[N];
int idx;
void quick_sort(int l,int r)
{
    if(l >= r)return;
    int i = l - 1, j = r + 1;
    int x = qt[(i + j) >> 1];
    while(i < j)
    {
        do i ++ ;while(qt[i] < x);
        do j -- ;while(qt[j] > x);
        if(i < j)swap(qt[i],qt[j]);
    }
    quick_sort(l,j);
    quick_sort(j + 1 , r);
}
void mer_met(int l, int r)
{
    if(l >= r) return;
    int mid = (l + r) >> 1;
    mer_met(l,mid);
    mer_met(mid+1,r);
    int wi = 0;
    int i = l,j = mid + 1;
    while(i <= mid && j <= r)
    {
        if(mt[i] < mt[j])pt[wi++] = mt[i++];
        else pt[wi++] = mt[j++];
    }
    while(i <= mid) pt[wi++] = mt[i++];
    while(j <= r)   pt[wi++] = mt[j++];

    for(int h = l, t = 0; h <= r ; h++ )
     mt[h] = pt[t++];
}
void heapsift(int t,int n)
{

    int i = t, j = t * 2;
    while(j<n)
    {
         if(j < n-1 &&ht[j]<ht[j+1])j++;
         if(ht[i]>ht[j]) break;
         else
         {

             swap(ht[i],ht[j]);
             i = j;
             j = 2*i + 1;
         }

    }
}
void  heapsort()
 {
     for(int i = n/2 ; i >= 0 ; i  -- )  heapsift(i,n);
     for(int i = 1;i < n - 1;i++)
     {

         swap(ht[0],ht[n-i]);
         heapsift(0,n-i);
     }
 }
int main()
{
   n = 1;
   while(n <= 1e7)
  {
    clock_t x1,y1,x2,y2,x3,y3;
    for(int i = 0 ; i < n ; i ++ ){

        qt[i] = rand()%10000;
        ht[i] = qt[i];
        mt[i] = qt[i];
    }
    if(n < (2 << 10))
    {
        cout << "数据规模是 ： "  << n <<endl;
        cout <<"排序前"<< endl;
        for(int i = 0; i <n ; i ++ )
        {
          cout << qt[i] <<" ";
          if(i%10==0 && i != 0) puts("");
        }
    }
    cout <<endl;
    x1 = clock();
    quick_sort(0,n-1);
    y1 = clock();
     y1-=x1;
    x2 = clock();
    mer_met(0,n-1);
    y2 = clock();
    y2=x2 ;
    x3 = clock();
    heapsort();
    y3 = clock();
    y3-=x3;
    counts[idx++] = {y1,y2,y3,n};
    if(n < (2 << 10))
    {
        cout <<"排序后"<< endl;
        for(int i = 0; i < n ; i ++ )
        {
            cout << qt[i] <<" ";
            if(i%10==0 && i != 0) cout <<endl;
        }
    }
    cout <<endl;
    n*=2;
  }
   for(int  i = 0; i < idx; i ++ )
   {

       cout << "数据规模是                "<<counts[i].t << endl;
       cout << "快排花费的时间(毫秒)      " << counts[i].q << endl;
       cout << "归并排序花费的时间（毫秒）" << counts[i].m << endl;
       cout << "堆排序花费的时间（毫秒）  " << counts[i].h << endl;
   }

  return 0;
}

空间复杂度比较：

归并排序最大， 快排与堆排序一个量级。
时间复杂度比较：
三者的时间复杂度都是 nlog(n)（以2为底）的量级
但是 从数据还有理论值来看： 快排<堆排序<归并排序。

（2）数据查找

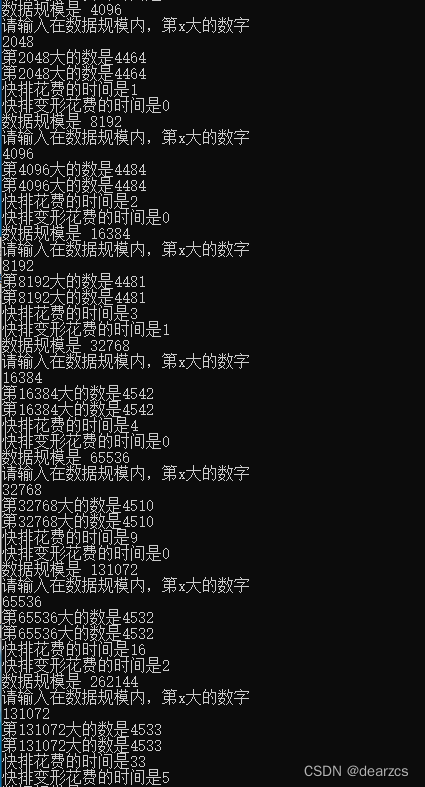
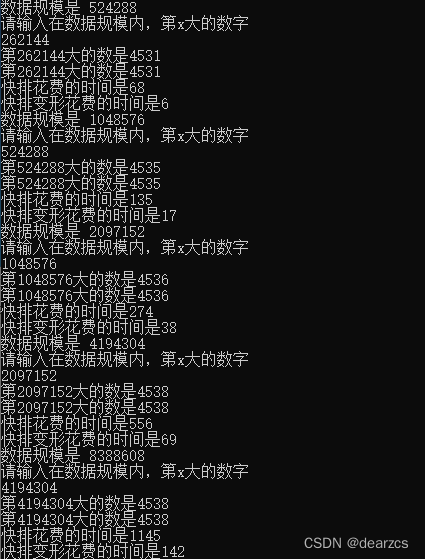
随机生成一个整数数组，数组规模N=16,32,64,128,256，512，…，用至少2种算法求数组的第i小元素，i可以由用户输入。做出图像，横坐标为数据规模，纵坐标为时间，分析你所做出的算法的时间复杂度及实际运行情况。所设计的两种算法至少一种时间复杂度要小于O(nlogn)。

数据查找结果：

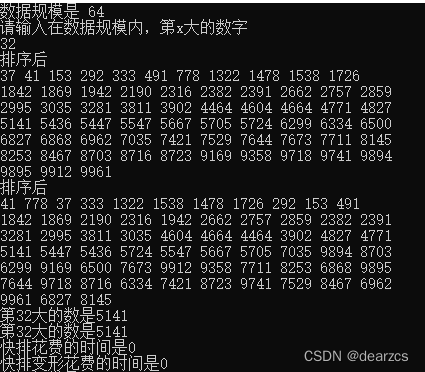
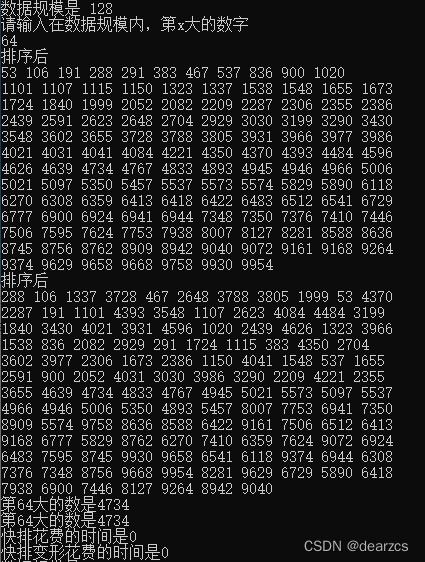
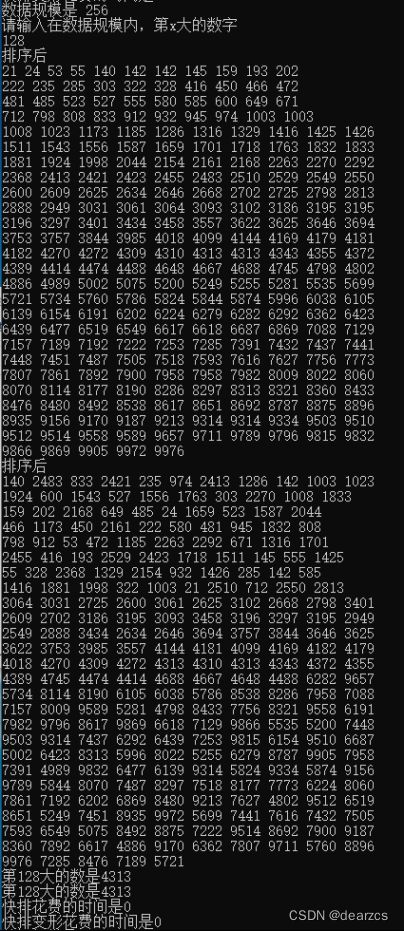
运行时间可视化

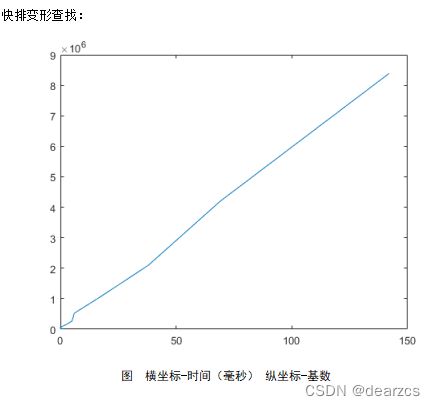
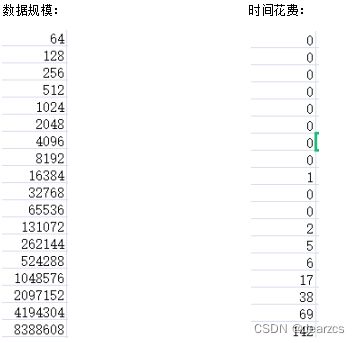
快排的平均时间复杂度为O(nlog(n)) (以2为底)以推导，所以这里不做描述

快排变形的查找：

最好情况：每趟最终结果是左侧与右侧等长，结合代码可以得出递推式的时间复杂度：   T(n) = T(n/2) + 7 + 9n/2  (n > 1)
       T(1) = 1
       满足分治推导式
       a  = 1,b = 2,k = 1.
       推出  T（n） = O(n)量级 
最坏情况：待排序数据每次划分后都是正序或者逆序，此时需要递归n-1次才能完成排序，每趟需要比较n - i次才能找到i的位置，
因此理想时间复杂度为：O（n^2）量级

推导出：时间复杂度量级在O(n) ~ O(n^2) 
因为快排已经展示过了所以这里不重复展示了，快排改良版比快排要快很多。

算法介绍：

快排：忽略（上个题目已给出算法）
快排变形查找：
功能：查找第x大的数
输入：待划分的记录序列data[first]~data[last]
输出：无
      1.设置划分区间：i = first; j = last;
      2.重复下述过程，直到i >= j;
         2.1 右侧扫描，直到data[j]小于data[i];将data[j]与data[i]交换，i++；
         2.2 左侧扫描，直到data[i]大于data[j];将data[i]与data[j]交换，j--;
      3.如果x < j对j点左侧进行快速排序；
      4.如果x > j对j点右侧进行快速排序；
	  5.如果x== j ，找到first~j 之间最大的值，与j处值交换。 

代码

题目二：
#include
#include
#include
#include
#include
using namespace std;
const int N = 1e7 +10;
int qt[N];
int qt1[N];
int n;
void quick_sort(int l,int r)
{
    if(l >= r)return;
    int i = l - 1, j = r + 1;
    int x = qt[(i + j) >> 1];
    while(i < j)
    {
        do i ++ ;while(qt[i] < x);
        do j -- ;while(qt[j] > x);
        if(i < j)swap(qt[i],qt[j]);
    }
    quick_sort(l,j);
    quick_sort(j + 1 , r);
}
void quick_find(int l, int r,int t)
{
    int x = qt1[(l + r) >> 1];
    int i = l - 1, j = r + 1;
    int ans = 0;
    while(i < j)
    {
        do i ++;while(qt1[i] < x);
        do j --;while(qt1[j] > x);
        if(i < j)swap(qt1[i],qt1[j]);

    }
    if(t < j) quick_find(l , j , t);
    if(t > j) quick_find(j + 1 , r,t);
    if(t == j)
    {
        int s = 0;
        int t = 0;
        for(int i = l ; i <= j; i++ )
            if(qt1[i] > s)
            {
                s = qt1[i];
                t = i;
            }
        swap(qt1[j],qt1[t]);
        return ;
    }


}
int main()
{
   n = 64;
   while(n <= 1e7)
  {
    clock_t x1,y1,x2,y2;
    for(int i = 0 ; i < n ; i ++ ){

        qt[i] = rand()%10000;
         qt1[i] = qt[i];
    }
    if(n <= (1 << 1))
    {
        cout << "排序前" <<endl;
        for(int i = 0; i < n ; i ++ )
        {
            cout << qt[i] << " ";
            if(i % 10 == 0 && i != 0) puts("");
        }
         cout << endl;
    }

    int x;
    cout << "数据规模是 " << n << endl;
    cout << "请输入在数据规模内，第x大的数字" << endl;
    cin >> x;
    x1 = clock();
    quick_sort(0,n-1);
    y1 = clock();
    y1-=x1;
     x2 = clock();
    quick_find(0,n-1,x-1);
    y2 = clock();
    y2-=x2;
     if(n <= (1 << 11))
    {
        cout << "排序后" <<endl;
        for(int i = 0; i < n ; i ++ )
        {
            cout << qt[i] << " ";
            if(i % 10 == 0 && i != 0) puts("");
        }
        cout << endl;
    }
         if(n <= (1 << 11))
    {
        cout << "排序后" <<endl;
        for(int i = 0; i < n ; i ++ )
        {
            cout << qt1[i] << " ";
            if(i % 10 == 0 && i != 0) puts("");
        }
        cout << endl;
    }
    cout << "第"<< x <<"大的数是" << qt[x-1] << endl;
    cout << "第"<< x <<"大的数是" << qt1[x-1] << endl;
    cout << "快排花费的时间是"  << y1 <<endl;
    cout << "快排变形花费的时间是" << y2 <<endl;
    n*=2;
  }
  return 0;
}