_42LeetCode代码随想录算法训练营第四十二天-动态规划 | 121.买卖股票的最佳时机、122.买卖股票的最佳时机II
_42LeetCode代码随想录算法训练营第四十二天-动态规划 | 121.买卖股票的最佳时机、122.买卖股票的最佳时机II
题目列表
- 121.买卖股票的最佳时机
- 122.买卖股票的最佳时机II
121.买卖股票的最佳时机
代码随想录地址:https://programmercarl.com/0121.%E4%B9%B0%E5%8D%96%E8%82%A1%E7%A5%A8%E7%9A%84%E6%9C%80%E4%BD%B3%E6%97%B6%E6%9C%BA.html
题目
给定一个数组 prices ,它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。
你只能选择 某一天 买入这只股票,并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。
返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润,返回 0 。
示例 1:
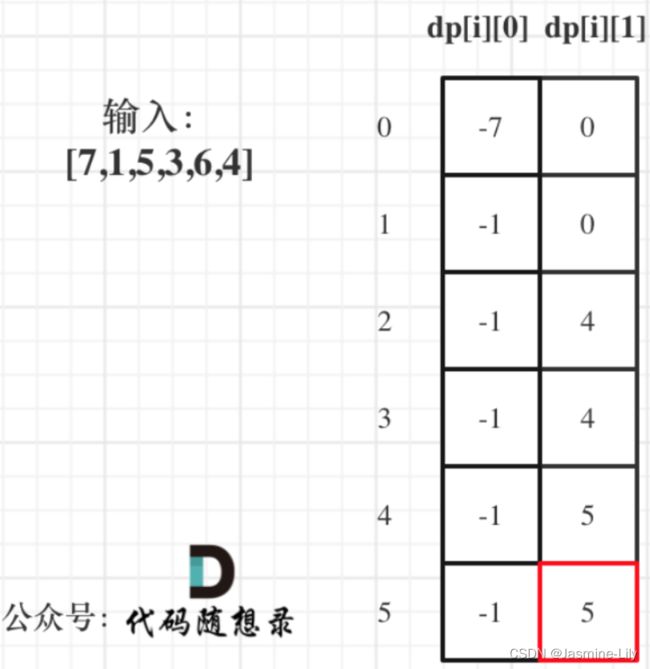
输入:[7,1,5,3,6,4]
输出:5
解释:在第 2 天(股票价格 = 1)的时候买入,在第 5 天(股票价格 = 6)的时候卖出,最大利润 = 6-1 = 5 。
注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格;同时,你不能在买入前卖出股票。
示例 2:
输入:prices = [7,6,4,3,1]
输出:0
解释:在这种情况下, 没有交易完成, 所以最大利润为 0。
提示:
- 1 <= prices.length <= 1 0 5 10^5 105
- 0 <= prices[i] <= 1 0 4 10^4 104
思路
动规五部曲:
- 确定dp数组(dp table)以及下标的含义
dp[i] [0] 表示第i天持有股票所得最多现金 ,这里的持有包括之前就持有或者今天买了股票。
如果持有股票,在本题中,现金就是负数。
dp[i] [1] 表示第i天不持有股票所得最多现金,这里包括一直未购买、之前卖掉或者今天卖掉股票。
- 确定递推公式
如果第i天持有股票即dp[i] [0], 那么可以由两个状态推出来
- 第i-1天就持有股票,那么就保持现状,所得现金就是昨天持有股票的所得现金 即:dp[i - 1] [0]
- 第i天买入股票,所得现金就是买入今天的股票后所得现金即:-prices[i]
那么dp[i] [0]应该选所得现金最大的,所以dp[i] [0] = max(dp[i - 1] [0], -prices[i]);
如果第i天不持有股票即dp[i] [1], 也可以由两个状态推出来
- 第i-1天就不持有股票,那么就保持现状,所得现金就是昨天不持有股票的所得现金 即:dp[i - 1] [1]
- 第i天卖出股票,所得现金就是按照今天股票价格卖出后所得现金即:prices[i] + dp[i - 1] [0]
同样dp[i] [1]取最大的,dp[i] [1] = max(dp[i - 1] [1], prices[i] + dp[i - 1] [0])。
- dp数组如何初始化
由递推公式可以看出dp数组都是要从dp[0] [0]和dp[0] [1]推导出来。
那么dp[0] [0]表示第0天持有股票,此时的持有股票就一定是买入股票了,因为不可能有前一天推出来,所以dp[0] [0] -= prices[0];
dp[0] [1]表示第0天不持有股票,不持有股票那么现金就是0,所以dp[0] [1] = 0;
- 遍历顺序
由递推公式可知是从前往后遍历。
- 动态分析dp数组
代码
暴力解法
- 时间复杂度:O(n^2)
- 空间复杂度:O(1)
两层for循环
class Solution {
public:
int maxProfit(vector<int>& prices) {
int result = 0;
for (int i = 0; i < prices.size(); i++) {
for (int j = i + 1; j < prices.size(); j++){
result = max(result, prices[j] - prices[i]);
}
}
return result;
}
};
贪心解法
- 时间复杂度:O(n)
- 空间复杂度:O(1)
取最左最小值,取最右最大值。
class Solution {
public:
int maxProfit(vector<int>& prices) {
int low = INT_MAX;
int result = 0;
for (int i = 0; i < prices.size(); i++) {
low = min(low, prices[i]); // 取最左最小价格
result = max(result, prices[i] - low); // 直接取最大区间利润
}
return result;
}
};
动态规划
空间复杂度较高的代码:
- 时间复杂度:O(n)
- 空间复杂度:O(n)
/*
* @lc app=leetcode.cn id=121 lang=cpp
*
* [121] 买卖股票的最佳时机
*/
// @lc code=start
class Solution {
public:
int maxProfit(vector<int>& prices) {
//定义dp数组,dp[i][1]表示第i天不持有股票,dp[i][0]表示第i天持有股票
vector<vector<int>> dp(prices.size(), vector<int>(2));
//初始化dp数组
dp[0][1] = 0;//第0天不持有股票
dp[0][0] = -prices[0];//第0天持有股票
//遍历
for(int i = 1; i < prices.size(); i++)
{
//第i天不持有股票:之前不持有 或者 之前持有第i天卖出
dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] + prices[i]);
//第i天持有股票:之前持有 或者 第i天买入
dp[i][0] = max(dp[i - 1][0], -prices[i]);
}
return dp[prices.size() - 1][1];
}
};
// @lc code=end
从递推公式可以看出,dp[i]只是依赖于dp[i - 1]的状态。
那么我们只需要记录 当前天的dp状态和前一天的dp状态就可以了,可以使用滚动数组来节省空间。
空间复杂度较低的代码:
- 时间复杂度:O(n)
- 空间复杂度:O(1)
// 版本二
class Solution {
public:
int maxProfit(vector<int>& prices) {
int len = prices.size();
vector<vector<int>> dp(2, vector<int>(2)); // 注意这里只开辟了一个2 * 2大小的二维数组
dp[0][0] -= prices[0];//持有
dp[0][1] = 0;//不持有
for (int i = 1; i < len; i++) {
dp[i % 2][0] = max(dp[(i - 1) % 2][0], -prices[i]);
dp[i % 2][1] = max(dp[(i - 1) % 2][1], prices[i] + dp[(i - 1) % 2][0]);
}
return dp[(len - 1) % 2][1];
}
};
122.买卖股票的最佳时机II
代码随想录地址:https://programmercarl.com/0122.%E4%B9%B0%E5%8D%96%E8%82%A1%E7%A5%A8%E7%9A%84%E6%9C%80%E4%BD%B3%E6%97%B6%E6%9C%BAII%EF%BC%88%E5%8A%A8%E6%80%81%E8%A7%84%E5%88%92%EF%BC%89.html
题目
给你一个整数数组 prices ,其中 prices[i] 表示某支股票第 i 天的价格。
在每一天,你可以决定是否购买和/或出售股票。你在任何时候 最多 只能持有 一股 股票。你也可以先购买,然后在 同一天 出售。
返回 你能获得的 最大 利润 。
示例 1:
输入:prices = [7,1,5,3,6,4]
输出:7
解释:在第 2 天(股票价格 = 1)的时候买入,在第 3 天(股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5 - 1 = 4 。
随后,在第 4 天(股票价格 = 3)的时候买入,在第 5 天(股票价格 = 6)的时候卖出, 这笔交易所能获得利润 = 6 - 3 = 3 。
总利润为 4 + 3 = 7 。
示例 2:
输入:prices = [1,2,3,4,5]
输出:4
解释:在第 1 天(股票价格 = 1)的时候买入,在第 5 天 (股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5 - 1 = 4 。
总利润为 4 。
示例 3:
输入:prices = [7,6,4,3,1]
输出:0
解释:在这种情况下, 交易无法获得正利润,所以不参与交易可以获得最大利润,最大利润为 0 。
提示:
- 1 <= prices.length <= 3 * 1 0 4 10^4 104
- 0 <= prices[i] <= 1 0 4 10^4 104
思路
与121.买卖股票的最佳时机的唯一不同在于买入股票时,手里的金额可能不为0。
代码
贪心解法
/*
* @lc app=leetcode.cn id=122 lang=cpp
*
* [122] 买卖股票的最佳时机 II
*/
// @lc code=start
class Solution {
public:
int maxProfit(vector<int>& prices) {
int res = 0;
for(int i = 1; i < prices.size(); i++)
{
if(prices[i] > prices[i - 1])
res += (prices[i] - prices[i - 1]);
}
return res;
}
};
// @lc code=end
动态规划代码
感觉贪心解法更简单。
- 时间复杂度:O(n)
- 空间复杂度:O(n)
/*
* @lc app=leetcode.cn id=122 lang=cpp
*
* [122] 买卖股票的最佳时机 II
*/
// @lc code=start
class Solution {
public:
int maxProfit(vector<int>& prices) {
//定义dp数组,dp[i][0]表示第i天持有股票的最大利润
//dp[i][1]表示第i天不持有股票的最大利润
vector<vector<int>> dp(prices.size(), vector<int>(2, 0));
//dp数组初始化
dp[0][0] = -prices[0];//第0天买入股票,即可持有股票
dp[0][1] = 0;//第0天不买入股票,即可不持有股票
//遍历
for(int i = 1; i < prices.size(); i++)
{
//此处为 与 121.买卖股票的最佳时机 的最大不同
//本题可以多次购买股票,因此买入股票之前可能是有钱的
//第i天持有股票:之前就持有 之前不持有今天买入
dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] - prices[i]);
//第i天不持有股票:之前就不持有 之前持有今天卖出
dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] + prices[i]);
}
return dp[prices.size() - 1][1];
}
};
// @lc code=end
可以使用滚动数组优化:
- 时间复杂度:O(n)
- 空间复杂度:O(1)
/*
* @lc app=leetcode.cn id=122 lang=cpp
*
* [122] 买卖股票的最佳时机 II
*/
// @lc code=start
class Solution {
public:
int maxProfit(vector<int>& prices) {
//定义dp数组,dp[i][0]表示第i天持有股票的最大利润
//dp[i][1]表示第i天不持有股票的最大利润
vector<vector<int>> dp(2, vector<int>(2, 0));
//dp数组初始化
dp[0][0] = -prices[0];//第0天买入股票,即可持有股票
dp[0][1] = 0;//第0天不买入股票,即可不持有股票
//遍历
for(int i = 1; i < prices.size(); i++)
{
//此处为 与 121.买卖股票的最佳时机 的最大不同
//本题可以多次购买股票,因此买入股票之前可能是有钱的
//第i天持有股票:之前就持有 之前不持有今天买入
dp[i % 2][0] = max(dp[(i - 1) % 2][0], dp[(i - 1) % 2][1] - prices[i]);
//第i天不持有股票:之前就不持有 之前持有今天卖出
dp[i % 2][1] = max(dp[(i - 1) % 2][1], dp[(i - 1) % 2][0] + prices[i]);
}
return dp[(prices.size() - 1) % 2][1];
}
};
// @lc code=end