使用Python实现二分查找算法及其应用场景详解
引言
二分查找是一种常用的搜索算法,它可以在有序数组中高效地查找指定元素。本文将详细介绍二分查找算法的原理、实现方法,并探讨其在实际应用场景中的使用。通过深入了解二分查找算法,你将能够更好地理解它的工作原理并灵活应用于各种问题中。
目录
引言
正文
二分查找算法原理
使用Python实现二分查找算法
三、二分查找算法的应用场景
示例代码
二分查找算法的时间复杂度分析
总结
参考资料
正文
二分查找算法原理
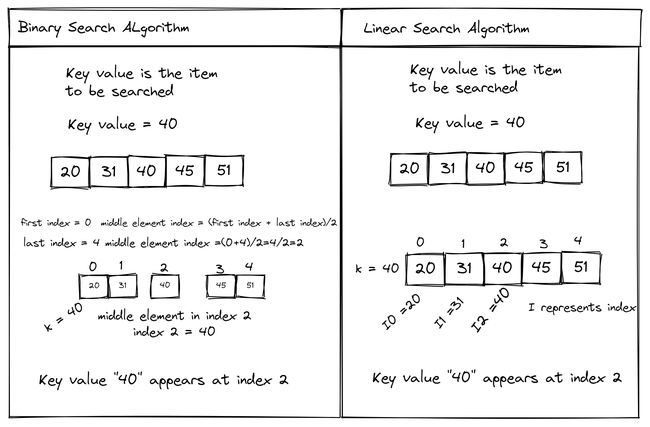
二分查找算法,也称为折半查找,是一种基于分治思想的搜索算法。它的基本原理是将有序数组分为两部分,并与目标元素进行比较,从而确定目标元素可能存在的区间。接着,根据比较结果,继续在较小或较大的那个区间内进行二分查找,直到找到目标元素或确定目标元素不存在。这种分而治之的策略使得二分查找算法的时间复杂度为 O(logN),在大规模数据集上具有高效性能。
下面详细介绍二分查找算法的原理:
1. 确定查找范围:
- 首先,我们需要有一个有序的数据集,通常是一个有序数组。
- 设定初始查找范围,一般是整个数组。使用两个指针,一个指向数组的起始位置,另一个指向数组的末尾位置。
2. 计算中间元素:
- 通过计算起始位置和末尾位置的中间位置,找到中间元素。可以使用整数除法运算来确定中间位置。
- 根据中间元素与目标元素的比较结果,可以确定目标元素可能存在的区间。
3. 比较与调整查找范围:
- 将目标元素与中间元素进行比较。
- 如果目标元素与中间元素相等,表示找到了目标元素,算法结束。
- 如果目标元素小于中间元素,说明目标元素可能在中间元素的左侧。此时,将末尾位置指针移动到中间元素的前一个位置,缩小查找范围为左半部分。
- 如果目标元素大于中间元素,说明目标元素可能在中间元素的右侧。此时,将起始位置指针移动到中间元素的后一个位置,缩小查找范围为右半部分。
- 根据比较结果,不断调整查找范围,重复执行步骤 2 和步骤 3,直到找到目标元素或确定目标元素不存在。
4. 完成查找:
- 如果起始位置指针大于末尾位置指针,表示查找范围为空,目标元素不存在于数组中,算法结束,返回查找失败的结果。
- 如果找到目标元素,算法结束,返回目标元素的索引。
使用Python实现二分查找算法
以下是使用Python实现二分查找算法的核心代码:
def binary_search(arr, target):
left = 0
right = len(arr) - 1
while left <= right:
mid = (left + right) // 2
if arr[mid] == target:
return mid
elif arr[mid] < target:
left = mid + 1
else:
right = mid - 1
return -1上述代码中,binary_search函数接受一个有序数组arr和目标元素target作为输入,并返回目标元素在数组中的索引。如果目标元素不存在于数组中,则返回-1。
三、二分查找算法的应用场景
-
查找有序数组中的特定元素 二分查找算法最常见的应用场景就是在有序数组中查找特定元素。例如,在一个存储学生分数的数组中,我们可以使用二分查找快速定位某个分数是否存在,或者找到分数所在的位置。这种应用场景可以提高查找效率,避免遍历整个数组进行线性查找。
-
寻找边界值 在某些情况下,我们需要找到有序数组中某个值的第一次出现位置或最后一次出现位置。二分查找算法可以被用于寻找边界值。通过稍作修改,我们可以找到第一个大于等于目标值的位置,或者最后一个小于等于目标值的位置。
-
数据范围的快速缩小 在某些算法问题中,我们需要在一个特定的数据范围内查找某个解。二分查找算法可以帮助我们快速缩小数据范围,以便更快地找到目标值。例如,在搜索某个函数的零点时,我们可以使用二分查找算法确定一个区间,并在该区间上进行迭代,逐步逼近零点。
-
旋转有序数组的搜索 在某些情况下,有序数组可能被旋转了若干次,即数组中的元素发生了循环移动。在这种情况下,二分查找仍然可以被应用于搜索目标元素。通过判断中间元素与边界元素的大小关系,我们可以确定目标元素位于旋转数组的哪一部分,并继续进行二分查找。
示例代码
在旋转有序数组中查找目标元素 下面是一个示例,演示如何在旋转有序数组中使用二分查找算法来查找目标元素。
def search_rotated_array(nums, target):
left = 0
right = len(nums) - 1
while left <= right:
mid = (left + right) // 2
if nums[mid] == target:
return mid
if nums[mid] >= nums[left]:
if target >= nums[left] and target < nums[mid]:
right = mid - 1
else:
left = mid + 1
else:
if target > nums[mid] and target <= nums[right]:
left = mid + 1
else:
right = mid - 1
return -1
nums = [6, 7, 8, 9, 1, 2, 3, 4, 5]
target = 2
result = search_rotated_array(nums, target)
if result != -1:
print("目标元素在旋转有序数组中的索引为:", result)
else:
print("目标元素不在旋转有序数组中。")在上述示例中,我们定义了一个旋转有序数组nums和目标元素target,然后调用search_rotated_array函数进行查找。如果目标元素存在于数组中,则打印其索引;否则,打印提示信息。
二分查找算法的时间复杂度分析
二分查找算法的时间复杂度为 O(logN),其中 N 表示有序数组的长度。这是由于每次查找都能将查找范围减半,因此在最坏情况下,需要进行 logN 次比较才能找到目标元素。
在二分查找算法中,每次迭代都将查找范围减半,因此可以表示为以下递归式: T(N) = T(N/2) + c
其中,T(N)表示解决一个长度为 N 的问题所需的时间,c 表示常数时间。
通过不断地将问题规模减半,可以得到以下推导: T(N) = T(N/2) + c = T(N/4) + c + c = T(N/8) + c + c + c = T(N/2^k) + k * c
当问题规模减小到 1 时,即 N/2^k = 1,解得 k = logN。
因此,二分查找算法的时间复杂度为 O(logN)。
需要注意的是,二分查找算法的时间复杂度只适用于静态数据集,即数据集不会频繁地插入、删除或修改元素。如果数据集经常发生变化,那么每次变化都需要重新排序,从而导致二分查找的效率降低。在这种情况下,可能需要考虑其他数据结构和算法来实现高效的查找。
综上所述,二分查找算法具有较低的时间复杂度,适用于静态有序数据集的查找问题。但在实际应用中,需要根据具体问题的特点和数据集的特征来选择合适的查找算法。
二分查找算法并不适用于所有问题。首先,要求使用二分查找算法的数据集必须是有序的。其次,二分查找算法的应用场景通常是针对静态数据集,即数据集不会频繁地插入、删除或修改元素。对于动态数据集,更适合使用其他数据结构和算法来进行高效的查找。
总结
本文详细介绍了二分查找算法的原理、Python实现方法以及在实际应用场景中的使用。二分查找算法是一种高效的搜索算法,在有序数组中定位特定元素时具有优势。通过深入了解二分查找算法,你将能够灵活应用它解决各种问题。希望本文对你理解和应用二分查找算法有所帮助。
参考资料
- 算法导论(原书第3版),Thomas H. Cormen等
- 《Python编程:从入门到实践》
- https://en.wikipedia.org/wiki/Binary_search_algorithm