2.技巧※(0x3f:从周赛中学算法 2022)
来自0x3f【从周赛中学算法 - 2022 年周赛题目总结(下篇)】:https://leetcode.cn/circle/discuss/WR1MJP/
技巧指一些比较套路的算法,包括双指针、滑动窗口、二分(主要指二分答案)、前缀和、差分、前后缀分解、位运算、二进制枚举、贡献法等。这些技巧相对容易掌握,想在周赛上分的同学可以优先学习这些内容。
顺带一提,我一般把窗口大小不固定的叫做双指针,窗口大小固定的叫做滑动窗口。
注:常见于周赛第二题(约占 18%)和第三题(约占 27%)。
| 题目 | 难度 | 备注 |
|---|---|---|
| 2483. 商店的最少代价 | 1495 | 前后缀分解 |
| 2461. 长度为 K 子数组中的最大和 | 1553 | 非常标准的滑动窗口题 |
| 2425. 所有数对的异或和 | 1622 | 贡献法 |
| 2420. 找到所有好下标 | 1695 | 前后缀分解 |
| 2397. 被列覆盖的最多行数 | 1719 | 二进制枚举 |
| 2401. 最长优雅子数组 | 1750 | 位运算与双指针结合的好题(暴力也可以过) |
| 2381. 字母移位 II | 1793 | 差分 |
| 2516. 每种字符至少取 K 个 | 1947 | 绝大多数双指针题目都是算子数组/子串,而这题是算的前缀+后缀,如此变形后要怎么做呢? |
| 2439. 最小化数组中的最大值 | 1954 | 二分答案之最小化最大值(看到最小和最大就要往二分答案上想) |
| 2517. 礼盒的最大甜蜜度 | 2020 | 二分答案 |
| 2444. 统计定界子数组的数目 | 2093 | 较为复杂的多指针题目,你能写出简洁的代码吗? |
2022上题目:
双指针
| 题目 | 题解 | 难度 | 备注 |
|---|---|---|---|
| 2271. 毯子覆盖的最多白色砖块数 | 题解 | 2021 | 双指针 |
| 2302. 统计得分小于 K 的子数组数目 | 题解 | 1808 | 双指针 |
二分
| 题目 | 题解 | 难度 | 备注 |
|---|---|---|---|
| 2141. 同时运行 N 台电脑的最长时间 | 题解 | 2265 | 二分答案 |
| 2251. 花期内花的数目 | 题解 | 2022 | 转换 |
| 2258. 逃离火灾 | 题解 | 2346 | 二分答案 |
文章目录
- 灵神-从周赛中学算法(技巧)
- 2022下
-
- [2483. 商店的最少代价](https://leetcode.cn/problems/minimum-penalty-for-a-shop/)
- [2461. 长度为 K 子数组中的最大和](https://leetcode.cn/problems/maximum-sum-of-distinct-subarrays-with-length-k/)
- [2425. 所有数对的异或和](https://leetcode.cn/problems/bitwise-xor-of-all-pairings/)
- [2420. 找到所有好下标](https://leetcode.cn/problems/find-all-good-indices/)
- [2397. 被列覆盖的最多行数](https://leetcode.cn/problems/maximum-rows-covered-by-columns/)
- [2401. 最长优雅子数组](https://leetcode.cn/problems/longest-nice-subarray/)
- [2381. 字母移位 II](https://leetcode.cn/problems/shifting-letters-ii/)
- [2516. 每种字符至少取 K 个](https://leetcode.cn/problems/take-k-of-each-character-from-left-and-right/)
- [2439. 最小化数组中的最大值](https://leetcode.cn/problems/minimize-maximum-of-array/)
- [2517. 礼盒的最大甜蜜度](https://leetcode.cn/problems/maximum-tastiness-of-candy-basket/)
-
- [1552. 两球之间的磁力](https://leetcode.cn/problems/magnetic-force-between-two-balls/)
- [2444. 统计定界子数组的数目](https://leetcode.cn/problems/count-subarrays-with-fixed-bounds/)
- 2022上
-
- 【重要】[2271. 毯子覆盖的最多白色砖块数](https://leetcode.cn/problems/maximum-white-tiles-covered-by-a-carpet/)
- [2302. 统计得分小于 K 的子数组数目](https://leetcode.cn/problems/count-subarrays-with-score-less-than-k/)
灵神-从周赛中学算法(技巧)
2022下
2483. 商店的最少代价
难度中等11
给你一个顾客访问商店的日志,用一个下标从 0 开始且只包含字符 'N' 和 'Y' 的字符串 customers 表示:
- 如果第
i个字符是'Y',它表示第i小时有顾客到达。 - 如果第
i个字符是'N',它表示第i小时没有顾客到达。
如果商店在第 j 小时关门(0 <= j <= n),代价按如下方式计算:
- 在开门期间,如果某一个小时没有顾客到达,代价增加
1。 - 在关门期间,如果某一个小时有顾客到达,代价增加
1。
请你返回在确保代价 最小 的前提下,商店的 最早 关门时间。
注意,商店在第 j 小时关门表示在第 j 小时以及之后商店处于关门状态。
示例 1:
输入:customers = "YYNY"
输出:2
解释:
- 第 0 小时关门,总共 1+1+0+1 = 3 代价。
- 第 1 小时关门,总共 0+1+0+1 = 2 代价。
- 第 2 小时关门,总共 0+0+0+1 = 1 代价。
- 第 3 小时关门,总共 0+0+1+1 = 2 代价。
- 第 4 小时关门,总共 0+0+1+0 = 1 代价。
在第 2 或第 4 小时关门代价都最小。由于第 2 小时更早,所以最优关门时间是 2 。
示例 2:
输入:customers = "NNNNN"
输出:0
解释:最优关门时间是 0 ,因为自始至终没有顾客到达。
示例 3:
输入:customers = "YYYY"
输出:4
解释:最优关门时间是 4 ,因为每一小时均有顾客到达。
提示:
1 <= customers.length <= 105customers只包含字符'Y'和'N'。
前缀和
class Solution {
public int bestClosingTime(String customers) {
int n = customers.length();
int[] s = new int[n+1];
// [0, 1, 2, 3, 4]
for(int i = 0; i < n; i++){
s[i+1] = s[i] + (customers.charAt(i) == 'Y' ? 1 : 0);
}
int res = 0;
int min = Integer.MAX_VALUE;
for(int i = 0; i <= n; i++){
int cur = 0;
cur += i - s[i]; // i小时前没有顾客来 + 1
cur += s[n] - s[i]; // i小时后有顾客来 + 1
if(cur < min){
min = cur;
res = i;
}
}
return res;
}
}
2461. 长度为 K 子数组中的最大和
难度中等32
给你一个整数数组 nums 和一个整数 k 。请你从 nums 中满足下述条件的全部子数组中找出最大子数组和:
- 子数组的长度是
k,且 - 子数组中的所有元素 各不相同 。
返回满足题面要求的最大子数组和。如果不存在子数组满足这些条件,返回 0 。
子数组 是数组中一段连续非空的元素序列。
示例 1:
输入:nums = [1,5,4,2,9,9,9], k = 3
输出:15
解释:nums 中长度为 3 的子数组是:
- [1,5,4] 满足全部条件,和为 10 。
- [5,4,2] 满足全部条件,和为 11 。
- [4,2,9] 满足全部条件,和为 15 。
- [2,9,9] 不满足全部条件,因为元素 9 出现重复。
- [9,9,9] 不满足全部条件,因为元素 9 出现重复。
因为 15 是满足全部条件的所有子数组中的最大子数组和,所以返回 15 。
示例 2:
输入:nums = [4,4,4], k = 3
输出:0
解释:nums 中长度为 3 的子数组是:
- [4,4,4] 不满足全部条件,因为元素 4 出现重复。
因为不存在满足全部条件的子数组,所以返回 0 。
提示:
1 <= k <= nums.length <= 1051 <= nums[i] <= 105
滑动窗口:当窗口值到达K的时候,统计答案,让左边界收缩
class Solution {
public long maximumSubarraySum(int[] nums, int k) {
long res = 0l, tmp = 0l;
int left = 0, right = 0;
int[] cnt = new int[100007];
while(right < nums.length){
cnt[nums[right]]++;
tmp += nums[right];
while(cnt[nums[right]] > 1){
tmp -= nums[left];
cnt[nums[left]]--;
left++;
}
if(right - left + 1 == k){
res = Math.max(res, tmp);
tmp -= nums[left];
cnt[nums[left]]--;
left++;
}
right++;
}
return res;
}
}
法二:用Map存储元素出现次数,当窗口值恒定为K,如果Map大小=k,则说明出现了k个不同的数字,统计答案
2425. 所有数对的异或和
难度中等13
给你两个下标从 0 开始的数组 nums1 和 nums2 ,两个数组都只包含非负整数。请你求出另外一个数组 nums3 ,包含 nums1 和 nums2 中 所有数对 的异或和(nums1 中每个整数都跟 nums2 中每个整数 恰好 匹配一次)。
请你返回 nums3 中所有整数的 异或和 。
示例 1:
输入:nums1 = [2,1,3], nums2 = [10,2,5,0]
输出:13
解释:
一个可能的 nums3 数组是 [8,0,7,2,11,3,4,1,9,1,6,3] 。
所有这些数字的异或和是 13 ,所以我们返回 13 。
示例 2:
输入:nums1 = [1,2], nums2 = [3,4]
输出:0
解释:
所有数对异或和的结果分别为 nums1[0] ^ nums2[0] ,nums1[0] ^ nums2[1] ,nums1[1] ^ nums2[0] 和 nums1[1] ^ nums2[1] 。
所以,一个可能的 nums3 数组是 [2,5,1,6] 。
2 ^ 5 ^ 1 ^ 6 = 0 ,所以我们返回 0 。
提示:
1 <= nums1.length, nums2.length <= 1050 <= nums1[i], nums2[j] <= 109
写几个找一下规律就好了:
对于 [a, b] 和 [c, d]
res = (a^c)^(a^d)^(b^c)^(b^d)
= (a^a)^(b^b)^(c^c)^(d^d)
= 0
对于 [a, b] 和 [c, d, e]
res = (a^c)^(a^d)^(a^e)^(b^c)^(b^d)^(b^e)
= (a^a^a)^(b^b^b)^(c^c)^(d^d)^(e^e)
= a^b
对于 [a,b,c] 和 [d, e]
res = (a^d)^(a^e)^(b^d)^(b^e)^(c^d)^(c^e)
= (a^a)^(b^b)^(c^c)^(d^d^d)^(e^e^e)
= d^e
可以发现:
- 如果 nums1 数组长度是偶数,nums2 中元素最终都会消为
0 - 如果 nums1 数组长度是奇数,nums2 会剩下
其每个元素的异或和
分别对 num1 和 num2 应用以上发现:
- 对于 [a, b] 和 [c, d],nums1 偶 nums2 偶,结果 =
0 ^ 0=0 - 对于 [a, b] 和 [c, d, e],nums1 偶 nums2 奇,结果 =
0 ^ nums1 每个元素的异或和=a^b - 对于 [a, b, c] 和 [d, e],nums1 奇 nums2 偶,结果 =
nums2 每个元素的异或和 ^ 0=d^e
class Solution {
// 由于答案是一大堆数字的异或和,根据贡献法的思想,
// 我们可以讨论每个数字在这一大堆数字中出现了多少次,对答案的贡献是多少。
// 对于 nums1[i],由于要与 nums2[i] 每个元素异或一次,因此nums1[i]出现了len(nums2[i])次
// 由于一个元素异或他自己=0,因此如果m是偶数,nums1[i]对答案贡献是0,否则就是nums1[i]
public int xorAllNums(int[] nums1, int[] nums2) {
int res = 0;
if(nums1.length % 2 != 0)
for(int n : nums2) res ^= n;
if(nums2.length % 2 != 0)
for(int n : nums1) res ^= n;
return res;
}
}
2420. 找到所有好下标
难度中等33收藏分享切换为英文接收动态反馈
给你一个大小为 n 下标从 0 开始的整数数组 nums 和一个正整数 k 。
对于 k <= i < n - k 之间的一个下标 i ,如果它满足以下条件,我们就称它为一个 好 下标:
- 下标
i之前 的k个元素是 非递增的 。 - 下标
i之后 的k个元素是 非递减的 。
按 升序 返回所有好下标。
示例 1:
输入:nums = [2,1,1,1,3,4,1], k = 2
输出:[2,3]
解释:数组中有两个好下标:
- 下标 2 。子数组 [2,1] 是非递增的,子数组 [1,3] 是非递减的。
- 下标 3 。子数组 [1,1] 是非递增的,子数组 [3,4] 是非递减的。
注意,下标 4 不是好下标,因为 [4,1] 不是非递减的。
示例 2:
输入:nums = [2,1,1,2], k = 2
输出:[]
解释:数组中没有好下标。
提示:
n == nums.length3 <= n <= 1051 <= nums[i] <= 1061 <= k <= n / 2
前缀和 + 后缀和预处理
class Solution {
public List<Integer> goodIndices(int[] nums, int k) {
int n = nums.length;
int[] suf = new int[n+1]; // suf[i]记录i位置后缀有多少非递减的
int[] pre = new int[n+1]; // pre[i]记录i位置前缀有多少非递增的
pre[0] = 1;
for(int i = 1; i < n; i++)
pre[i] = nums[i] <= nums[i-1] ? pre[i-1] + 1 : 1;
suf[n-1] = 1;
for(int i = n-2; i >= 0; i--)
suf[i] = nums[i] <= nums[i+1] ? suf[i+1] + 1 : 1;
List<Integer> res = new ArrayList<>();
for(int i = k; i < n-k; i++){
// 枚举i位置,注意不包括i
if(pre[i-1] >= k && suf[i+1] >= k) res.add(i);
}
return res;
}
}
2397. 被列覆盖的最多行数
难度中等35
给你一个下标从 0 开始的 m x n 二进制矩阵 mat 和一个整数 cols ,表示你需要选出的列数。
如果一行中,所有的 1 都被你选中的列所覆盖,那么我们称这一行 被覆盖 了。
请你返回在选择 cols 列的情况下,被覆盖 的行数 最大 为多少。
示例 1:
输入:mat = [[0,0,0],[1,0,1],[0,1,1],[0,0,1]], cols = 2
输出:3
解释:
如上图所示,覆盖 3 行的一种可行办法是选择第 0 和第 2 列。
可以看出,不存在大于 3 行被覆盖的方案,所以我们返回 3 。
示例 2:
输入:mat = [[1],[0]], cols = 1
输出:2
解释:
选择唯一的一列,两行都被覆盖了,原因是整个矩阵都被覆盖了。
所以我们返回 2 。
提示:
m == mat.lengthn == mat[i].length1 <= m, n <= 12mat[i][j]要么是0要么是1。1 <= cols <= n
class Solution {
public int maximumRows(int[][] matrix, int numSelect) {
int m = matrix.length, n = matrix[0].length;
int state = 1 << n; //state = 2^n-1
int[] mask = new int[m];
//把每一行看成一个数字
//预处理一个行的掩码mask,记录行1出现的位置
for(int i = 0; i < m; i++){
for(int j = 0; j < n; j++){
if(matrix[i][j] == 1){
mask[i] ^= (1 << j);
}
}
}
int res = 0;
// 一开始还想dfs枚举出所有大小为k的列组合,实际上只用遍历1<
for(int i = 0; i < state; i++){//遍历{空集-{0,1,2,..,n-1}所有的集合}
if(Integer.bitCount(i) == numSelect){
//只有选中cols列时才判断覆盖了多少行
int count = 0;
for(int x : mask){
// 逐行进行判断,统计个数
// i=101 ; ~i=010 ; x = 101 ; (~i)&x = 000;
if(((~i)&x) == 0){
count++;
}
}
res = Math.max(res, count);
}
}
return res;
}
}
2401. 最长优雅子数组
难度中等40
给你一个由 正 整数组成的数组 nums 。
如果 nums 的子数组中位于 不同 位置的每对元素按位 **与(AND)**运算的结果等于 0 ,则称该子数组为 优雅 子数组。
返回 最长 的优雅子数组的长度。
子数组 是数组中的一个 连续 部分。
**注意:**长度为 1 的子数组始终视作优雅子数组。
示例 1:
输入:nums = [1,3,8,48,10]
输出:3
解释:最长的优雅子数组是 [3,8,48] 。子数组满足题目条件:
- 3 AND 8 = 0
- 3 AND 48 = 0
- 8 AND 48 = 0
可以证明不存在更长的优雅子数组,所以返回 3 。
示例 2:
输入:nums = [3,1,5,11,13]
输出:1
解释:最长的优雅子数组长度为 1 ,任何长度为 1 的子数组都满足题目条件。
提示:
1 <= nums.length <= 1051 <= nums[i] <= 109
核心思想:双指针 + 位运算
class Solution {
public int longestNiceSubarray(int[] nums) {
int n = nums.length;
int left = 0, right = 0;
int res = 0;
int cnt = 0;
while(right < n){
while((cnt & nums[right]) != 0){
cnt ^= nums[left];
left++;
}
cnt ^= nums[right];
right++;
res = Math.max(res, (right-left));
}
return res;
}
}
2381. 字母移位 II
难度中等16
给你一个小写英文字母组成的字符串 s 和一个二维整数数组 shifts ,其中 shifts[i] = [starti, endi, directioni] 。对于每个 i ,将 s 中从下标 starti 到下标 endi (两者都包含)所有字符都进行移位运算,如果 directioni = 1 将字符向后移位,如果 directioni = 0 将字符向前移位。
将一个字符 向后 移位的意思是将这个字符用字母表中 下一个 字母替换(字母表视为环绕的,所以 'z' 变成 'a')。类似的,将一个字符 向前 移位的意思是将这个字符用字母表中 前一个 字母替换(字母表是环绕的,所以 'a' 变成 'z' )。
请你返回对 s 进行所有移位操作以后得到的最终字符串。
示例 1:
输入:s = "abc", shifts = [[0,1,0],[1,2,1],[0,2,1]]
输出:"ace"
解释:首先,将下标从 0 到 1 的字母向前移位,得到 s = "zac" 。
然后,将下标从 1 到 2 的字母向后移位,得到 s = "zbd" 。
最后,将下标从 0 到 2 的字符向后移位,得到 s = "ace" 。
示例 2:
输入:s = "dztz", shifts = [[0,0,0],[1,1,1]]
输出:"catz"
解释:首先,将下标从 0 到 0 的字母向前移位,得到 s = "cztz" 。
最后,将下标从 1 到 1 的字符向后移位,得到 s = "catz" 。
提示:
1 <= s.length, shifts.length <= 5 * 104shifts[i].length == 30 <= starti <= endi < s.length0 <= directioni <= 1s只包含小写英文字母。
题解:差分数组
那么现在有一个任务:对数组a区间[left,right]每个元素加一个常数c。这时可以利用原数组就是差分数组的前缀和这个特性,来解决这个问题。
对于b数组,只需要执行b[left] += c, b[right+1] −= c
如何得到更新后的数组元素值? 只需要累加即可:第i位值sum :sum += b[i]
class Solution {
// 使用差分数组计算每个位置总共左移或者右移的位数
// 与现有的加和后取模得到最终的字符
public String shiftingLetters(String s, int[][] shifts) {
int n = s.length();
int[] diff = new int[n+1];
for(int i = 0; i < shifts.length; i++){
int from = shifts[i][0], to = shifts[i][1], d = shifts[i][2];
int add = d == 1 ? 1 : -1;
diff[from] += add;
diff[to+1] -= add;
}
int sum = 0;
char[] c = new char[n];
for(int i = 0; i < n; i++){
sum += diff[i];
c[i] = (char)(((((s.charAt(i) - 'a' + sum) % 26) + 26) % 26) + 'a');
}
return new String(c);
}
}
2516. 每种字符至少取 K 个
难度中等25
给你一个由字符 'a'、'b'、'c' 组成的字符串 s 和一个非负整数 k 。每分钟,你可以选择取走 s 最左侧 还是 最右侧 的那个字符。
你必须取走每种字符 至少 k 个,返回需要的 最少 分钟数;如果无法取到,则返回 -1 。
示例 1:
输入:s = "aabaaaacaabc", k = 2
输出:8
解释:
从 s 的左侧取三个字符,现在共取到两个字符 'a' 、一个字符 'b' 。
从 s 的右侧取五个字符,现在共取到四个字符 'a' 、两个字符 'b' 和两个字符 'c' 。
共需要 3 + 5 = 8 分钟。
可以证明需要的最少分钟数是 8 。
示例 2:
输入:s = "a", k = 1
输出:-1
解释:无法取到一个字符 'b' 或者 'c',所以返回 -1 。
提示:
1 <= s.length <= 105s仅由字母'a'、'b'、'c'组成0 <= k <= s.length
class Solution {
// aabaaaacaabc k = 2
// 前缀 后缀 答案
// baaaacaabc 10
// a baaaacaabc 11
// aa baaaacaabc 12
// aab caabc 8 // 找到了一个更短的前缀+后缀
// aaba caabc 9
// aabaa caabc 10
// ... ... ...
// 随着i的变大,j也会单调变大,因此可以从小到大枚举j,一边维护i的最大值
public int takeCharacters(String s, int k) {
int n = s.length();
if(n < 3 * k) return -1;
int[] arrs = new int[3];
char[] cs = s.toCharArray();
// 判断s中abc各有多少个
for(char c : cs)
arrs[c-'a']++;
// abc减去k后,还剩多少个(即不需要取走的字符数)
int leavea = arrs[0] - k;
int leaveb = arrs[1] - k;
int leavec = arrs[2] - k;
// 如果剩余的都为0,说明s整个都要取走 return n
if(leavea == 0 && leaveb == 0 && leavec == 0) return n;
// 如果有一个剩余<0,说明该字符不足k个
if(leavea < 0 || leaveb < 0 || leavec < 0) return -1;
// 滑动窗口 为s中的一段,满足arrs[i] > leave i,求得滑动窗口最大值,len - windows 为所求最小值
// right,n为后缀;0-left为前缀,从小到大枚举后缀的同时维护前缀
int left = 0, right = 0, max = 0;
arrs = new int[3];
while(right < n){
arrs[cs[right] - 'a']++;
// 当[left,right]时,再[0,left-1]和[right+1,n]前后缀中取不到abc任意k个,就需要缩短窗口值
while(arrs[0] > leavea || arrs[1] > leaveb || arrs[2] > leavec){
arrs[cs[left++] - 'a']--;
}
max = Math.max(max, right - left + 1);
right++;
}
return n - max;
}
}
2439. 最小化数组中的最大值
难度中等40
给你一个下标从 0 开始的数组 nums ,它含有 n 个非负整数。
每一步操作中,你需要:
- 选择一个满足
1 <= i < n的整数i,且nums[i] > 0。 - 将
nums[i]减 1 。 - 将
nums[i - 1]加 1 。
你可以对数组执行 任意 次上述操作,请你返回可以得到的 nums 数组中 最大值 最小 为多少。
示例 1:
输入:nums = [3,7,1,6]
输出:5
解释:
一串最优操作是:
1. 选择 i = 1 ,nums 变为 [4,6,1,6] 。
2. 选择 i = 3 ,nums 变为 [4,6,2,5] 。
3. 选择 i = 1 ,nums 变为 [5,5,2,5] 。
nums 中最大值为 5 。无法得到比 5 更小的最大值。
所以我们返回 5 。
示例 2:
输入:nums = [10,1]
输出:10
解释:
最优解是不改动 nums ,10 是最大值,所以返回 10 。
提示:
n == nums.length2 <= n <= 1050 <= nums[i] <= 109
二分答案:
class Solution {
public int minimizeArrayValue(int[] nums) {
int n = nums.length;
int max = 0;
for(int i = 0; i < n; i++) max = Math.max(nums[i], max);
int left = 0, right = max;
while(left < right){
int mid = (left + right) / 2;
if(!check(nums, mid)) left = mid + 1;
else right = mid;
}
return right;
}
// nums数组中能不能最大值top
public boolean check(int[] nums, int top){
int n = nums.length;
int right = n-1;
double diff = 0;
while(right > 0){ // 从后往前模拟
// 如果当前数字 + 后一位额外添加的数字 > top,则需要nums[right] + diff - top补给前一位
if(nums[right] + diff > top) {
diff = (double)(nums[right] + diff - top);
}else{
diff = 0;
}
right--;
}
// 最后负担都再nums[0]上,看nums[0]能否满足要求(能不能最大值top)
return nums[0] + diff <= top;
}
}
2517. 礼盒的最大甜蜜度
难度中等31
给你一个正整数数组 price ,其中 price[i] 表示第 i 类糖果的价格,另给你一个正整数 k 。
商店组合 k 类 不同 糖果打包成礼盒出售。礼盒的 甜蜜度 是礼盒中任意两种糖果 价格 绝对差的最小值。
返回礼盒的 最大 甜蜜度*。*
示例 1:
输入:price = [13,5,1,8,21,2], k = 3
输出:8
解释:选出价格分别为 [13,5,21] 的三类糖果。
礼盒的甜蜜度为 min(|13 - 5|, |13 - 21|, |5 - 21|) = min(8, 8, 16) = 8 。
可以证明能够取得的最大甜蜜度就是 8 。
示例 2:
输入:price = [1,3,1], k = 2
输出:2
解释:选出价格分别为 [1,3] 的两类糖果。
礼盒的甜蜜度为 min(|1 - 3|) = min(2) = 2 。
可以证明能够取得的最大甜蜜度就是 2 。
示例 3:
输入:price = [7,7,7,7], k = 2
输出:0
解释:从现有的糖果中任选两类糖果,甜蜜度都会是 0 。
提示:
1 <= price.length <= 1051 <= price[i] <= 1092 <= k <= price.length
class Solution {
// 「能力检测二分」
// 由于随着甜蜜度的增大,能选择的糖果数量变小,有单调性,所以可以用二分答案来做。
// 疑问:那个check里面的大于等于,如果你所有的元素都是大于那个d,
// 而没有等于的话,他取min的时候不也是不符合的嘛?
// 解答:二分结束的位置等号一定是成立的。
// 因为从「能选至少 k 个」到「选不到 k 个」之间,一定会经过「能选恰好k个」。
public int maximumTastiness(int[] price, int k) {
Arrays.sort(price);
int n = price.length;
int left = 0, right = price[n-1] - price[0];
while(left < right){ // (left, right]
// 这里左开右闭模型(当mid满足条件仍然是要mid的)
// 因此mid在取值时要向上取整即(left + right + 1)/2
int mid = (left + right + 1) >> 1;
if(check(price, k, mid)) left = mid;
else right = mid - 1;
}
return left;
}
// 贪心: 一旦与上一个选中糖果的差值大于等于gap, 就取这个糖果
public boolean check(int[] price, int k, int gap){
int cnt = 1; // 最小的糖果一定会取
int pre = price[0];
for(int i = 1; i < price.length; i++){
// 如果两个下标的甜蜜读
if(price[i] - pre >= gap){
cnt++;
pre = price[i];
}
if(cnt >= k)// 取到了k个,提前结束
return true;
}
return cnt >= k;
}
}
1552. 两球之间的磁力
难度中等155
在代号为 C-137 的地球上,Rick 发现如果他将两个球放在他新发明的篮子里,它们之间会形成特殊形式的磁力。Rick 有 n 个空的篮子,第 i 个篮子的位置在 position[i] ,Morty 想把 m 个球放到这些篮子里,使得任意两球间 最小磁力 最大。
已知两个球如果分别位于 x 和 y ,那么它们之间的磁力为 |x - y| 。
给你一个整数数组 position 和一个整数 m ,请你返回最大化的最小磁力。
示例 1:
输入:position = [1,2,3,4,7], m = 3
输出:3
解释:将 3 个球分别放入位于 1,4 和 7 的三个篮子,两球间的磁力分别为 [3, 3, 6]。最小磁力为 3 。我们没办法让最小磁力大于 3 。
示例 2:
输入:position = [5,4,3,2,1,1000000000], m = 2
输出:999999999
解释:我们使用位于 1 和 1000000000 的篮子时最小磁力最大。
提示:
n == position.length2 <= n <= 10^51 <= position[i] <= 10^9- 所有
position中的整数 互不相同 。 2 <= m <= position.length
题解:同样的题目 不同的题干
class Solution {
public int maxDistance(int[] position, int m) {
Arrays.sort(position);
int left = 0, right = position[position.length-1] - position[0];
while(left < right){
int mid = left + (right -left) / 2 + 1;
if(check(position, m, mid)) left = mid;
else right = mid - 1;
}
return right;
}
public boolean check(int[] position, int m, int gap){
int cnt = 1;
int pre = position[0];
for(int i = 1; i < position.length; i++){
if(position[i] - pre >= gap){
cnt += 1;
pre = position[i];
}
if(cnt >= m) return true;
}
return cnt >= m;
}
}
2444. 统计定界子数组的数目
难度困难74
给你一个整数数组 nums 和两个整数 minK 以及 maxK 。
nums 的定界子数组是满足下述条件的一个子数组:
- 子数组中的 最小值 等于
minK。 - 子数组中的 最大值 等于
maxK。
返回定界子数组的数目。
子数组是数组中的一个连续部分。
示例 1:
输入:nums = [1,3,5,2,7,5], minK = 1, maxK = 5
输出:2
解释:定界子数组是 [1,3,5] 和 [1,3,5,2] 。
示例 2:
输入:nums = [1,1,1,1], minK = 1, maxK = 1
输出:10
解释:nums 的每个子数组都是一个定界子数组。共有 10 个子数组。
提示:
2 <= nums.length <= 1051 <= nums[i], minK, maxK <= 106
class Solution {
// 把在[minK,maxK]之外的数字当成分割点,只需要考虑在两个相邻分割点之间的子数组
// ==> 双指针 枚举右端点,看左端点能落在哪些范围内
// 1. mini,最小值minK出现的位置 ; maxi,最大值mink出现的位置
// 2. i0, 上一个不在[minK,maxK]区间范围内的边界
// 取值 (Math.min(mini, maxi) - i0)
public long countSubarrays(int[] nums, int minK, int maxK) {
long res = 0l;
int n = nums.length, mini = -1, maxi = -1, i0 = -1;
for(int i = 0; i < n; i++){
int x = nums[i];
if(x == minK) mini = i;
if(x == maxK) maxi = i;
if(x < minK || x > maxK) i0 = i; // 子数组不能包含 nums[i0]
res += Math.max(Math.min(mini, maxi) - i0, 0);
}
return res;
}
}
2022上
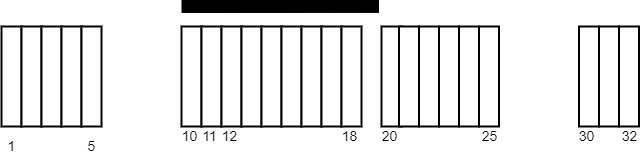
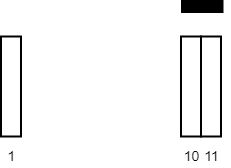
【重要】2271. 毯子覆盖的最多白色砖块数
难度中等45
给你一个二维整数数组 tiles ,其中 tiles[i] = [li, ri] ,表示所有在 li <= j <= ri 之间的每个瓷砖位置 j 都被涂成了白色。
同时给你一个整数 carpetLen ,表示可以放在 任何位置 的一块毯子。
请你返回使用这块毯子,最多 可以盖住多少块瓷砖。
示例 1:
输入:tiles = [[1,5],[10,11],[12,18],[20,25],[30,32]], carpetLen = 10
输出:9
解释:将毯子从瓷砖 10 开始放置。
总共覆盖 9 块瓷砖,所以返回 9 。
注意可能有其他方案也可以覆盖 9 块瓷砖。
可以看出,瓷砖无法覆盖超过 9 块瓷砖。
示例 2:
输入:tiles = [[10,11],[1,1]], carpetLen = 2
输出:2
解释:将毯子从瓷砖 10 开始放置。
总共覆盖 2 块瓷砖,所以我们返回 2 。
提示:
1 <= tiles.length <= 5 * 104tiles[i].length == 21 <= li <= ri <= 1091 <= carpetLen <= 109tiles互相 不会重叠 。
方法一:排序 + 前缀和 + 二分
https://leetcode.cn/problems/maximum-white-tiles-covered-by-a-carpet/solution/by-xjf-z-ll1k/
题目没有保证tiles数组是有序的,所以肯定要先对tiles数组进行排序,又由于tiles[i]不重叠,所以只需要按照tiles[i][0]排序即可
观察题目给出的示例1,我们发现只有当毯子处于li 位置(即每个连成片的瓷砖的头部)时,可以盖住最多的瓷砖。因为当毯子后移时,假设毯子的长度长于该区间的长度,中间会有一段原本能盖到瓷砖后移之后却盖不到瓷砖,当然尾部可能会有一段原本盖不到瓷砖后移之后能盖到瓷砖,但这只能抹平,不能超过。
所以我们只用将每个tiles[i][0]作为毯子可能的起始位置进行搜索。
之后,由于毯子长度固定,在确定了毯子的起始位置start后,我们也能找到毯子的结束位置end的下标。我们需要统计这一段区间内瓷砖的数量。如果一个一个去遍历,由于毯子长度最大可达1e9,肯定会超时,这时又要用到前缀和数组,这次的前缀和数组统计的是前i个区间,所包含的瓷砖的总数
class Solution {
// 前缀和 + 二分
public int maximumWhiteTiles(int[][] tiles, int carpetLen) {
Arrays.sort(tiles, (a, b) -> a[0] - b[0]);
// 定义pre[i]表示前i个区间锁包含的瓷砖数目
int[] pre = new int[tiles.length + 1];
for(int i = 0; i < tiles.length; i++){
// 注意pre[i] 表示 前i 项中的瓷砖个数因此用 tiles[i][1] - tile[i][0]
pre[i+1] = pre[i] + tiles[i][1] - tiles[i][0] + 1;
}
int ans = 0;
for(int i = 0; i < tiles.length; i++){
// 边界处理
if(tiles[i][0] + carpetLen > tiles[tiles.length - 1][1]){
ans = Math.max(ans, pre[tiles.length] - pre[i]);
break;
}
// 枚举左端点, 寻找地毯的右端点,大于地毯右端点的第一个tiles
int left = i, right = tiles.length, target = tiles[i][0] + carpetLen - 1;
while(left < right){
int mid = (left + right) >> 1;
if(tiles[mid][1] <= target) left = mid + 1;
else right = mid;
}
if(tiles[i][0] + carpetLen <= tiles[right][0])
ans = Math.max(ans, pre[right] - pre[i]);
else // 多出tiles[right][0] 一段, 除了pre[right] - pre[i] 还要加上多出的一段
ans = Math.max(ans,
pre[right] - pre[i] + tiles[i][0] + carpetLen - tiles[right][0]);
}
return ans;
}
}
时间复杂度:O(n*log(n))
方法二:贪心 + 双指针
https://leetcode.cn/problems/maximum-white-tiles-covered-by-a-carpet/solution/by-endlesscheng-kdy9/
将 tiles 按左端点 li 排序后,我们可以枚举毯子的摆放位置,然后计算毯子能覆盖多少块瓷砖。
实际上,毯子右端点放在一段瓷砖中间,是不如直接放在这段瓷砖右端点的 (因为从中间向右移动,能覆盖的瓷砖数不会减少) ,所以可以枚举每段瓷砖的右端点来摆放毯子的右端点。
这样就可以双指针了,左指针 left 需要满足其指向的那段瓷砖的右端点被毯子覆盖。
设毯子右端点在瓷砖段 i 上,则毯子左端点位于 tiles[i] - carpetLen +1,对于 left 需要满足
tiles[left][1] >= tiles[i][1] - carpetLen + 1
如果毯子左端点在瓷砖段 tiles[left] 内部,则覆盖的瓷砖数还需要额外减去这段瓷砖没被覆盖的部分,即减去
(tiles[i](1] - carpetLen + 1) - tiles[left][0]
class Solution {
/*
贪心+滑窗:
1.贪心证明:假设毯子左边缘位于某个区间中间,此时向右移动只会使得覆盖区间减少1或者0
向左移动只会使得覆盖区间增加1或者0,因此移动至区间左边界是最优的选择
2.滑窗方式:每次固定l指针然后找出区间覆盖到的区间,计算一次最大值
之后左指针主动右移一个区间,右指针被动右移至合适位置
最后的最大值就是结果
*/
public int maximumWhiteTiles(int[][] tiles, int carpetLen) {
Arrays.sort(tiles, (a, b) -> a[0] - b[0]);
int ans = 0, cover = 0, left = 0;
for(int[] t : tiles){
int tl = t[0], tr = t[1];
cover += tr - tl + 1;
while(tiles[left][1] + carpetLen - 1 < tr){
cover -= tiles[left][1] - tiles[left][0] + 1;
left += 1;
}
ans = Math.max(ans,
cover - Math.max(tr - carpetLen + 1 - tiles[left][0], 0)); // 0 表示毯子左端点不在瓷砖内的情况
}
return ans;
}
}
时间复杂度:O(nlogn),瓶颈在排序上
2302. 统计得分小于 K 的子数组数目
难度困难20
一个数组的 分数 定义为数组之和 乘以 数组的长度。
- 比方说,
[1, 2, 3, 4, 5]的分数为(1 + 2 + 3 + 4 + 5) * 5 = 75。
给你一个正整数数组 nums 和一个整数 k ,请你返回 nums 中分数 严格小于 k 的 非空整数子数组数目。
子数组 是数组中的一个连续元素序列。
示例 1:
输入:nums = [2,1,4,3,5], k = 10
输出:6
解释:
有 6 个子数组的分数小于 10 :
- [2] 分数为 2 * 1 = 2 。
- [1] 分数为 1 * 1 = 1 。
- [4] 分数为 4 * 1 = 4 。
- [3] 分数为 3 * 1 = 3 。
- [5] 分数为 5 * 1 = 5 。
- [2,1] 分数为 (2 + 1) * 2 = 6 。
注意,子数组 [1,4] 和 [4,3,5] 不符合要求,因为它们的分数分别为 10 和 36,但我们要求子数组的分数严格小于 10 。
示例 2:
输入:nums = [1,1,1], k = 5
输出:5
解释:
除了 [1,1,1] 以外每个子数组分数都小于 5 。
[1,1,1] 分数为 (1 + 1 + 1) * 3 = 9 ,大于 5 。
所以总共有 5 个子数组得分小于 5 。
提示:
1 <= nums.length <= 1051 <= nums[i] <= 1051 <= k <= 1015
题解:双指针( 一个困难题就这么A了???信心大增)
双指针使用前提:
-
子数组(连续);
-
有单调性。本题元素均为正数,这意味着只要某个子数组满足题目要求,在该子数组内的更短的子数组同样也满足题目要求。
做法:枚举子数组右端点,去看对应的合法左端点的个数,那么根据上面的前提 2,我们需要求出合法左端点的最小值。
class Solution {
public long countSubarrays(int[] nums, long k) {
long ans = 0;
int n = nums.length, left = 0;
long s = 0l;
long[] sum = new long[n+1];
for(int i = 0; i < n; i++)
sum[i+1] = sum[i] + nums[i];
// 由于区间越大,乘法结果只会增大不会减小,可以使用双指针
// 枚举以right-1为右端点的区间,查看[left,right-1]是否符合条件
for(int right = 1; right <= n; right++){
s = (sum[right] - sum[left]) * (right - left);
while(left < right && s >= k){
left += 1;
s = (sum[right] - sum[left]) * (right - left);
}
ans += (right - left); // 以right-1为右端点的区间,符合条件的[left,right-1]\[left+1,right-1]... right-left 个
}
return ans;
}
}
优化写法:
class Solution {
public long countSubarrays(int[] nums, long k) {
long ans = 0L, sum = 0L;
for(int left = 0, right = 0; right < nums.length; right++){
sum += nums[right];
while(sum * (right - left + 1) >= k)
sum -= nums[left++];
ans += right - left + 1;
}
return ans;
}
}
时间复杂度:O(n)