使用高斯混合模型拆分多模态分布

本文介绍如何使用高斯混合模型将一维多模态分布拆分为多个分布。

高斯混合模型（Gaussian Mixture Models，简称GMM）是一种在统计和机器学习领域中常用的概率模型，用于对复杂数据分布进行建模和分析。GMM 是一种生成模型，它假设观测数据是由多个高斯分布组合而成的，每个高斯分布称为一个分量，这些分量通过权重来控制其在数据中的贡献。

生成具有多模态分布的数据

当一个数据集显示出多个不同的峰值或模态时，通常会出现显示出多个不同的峰值或模态，每个模态代表分布中一个突出的数据点簇或集中。这些模式可以看作是数据值更可能出现的高密度区域。

我们将使用numpy生成的一维数组。

 import numpy as np
 
 dist_1 = np.random.normal(10, 3, 1000)
 dist_2 = np.random.normal(30, 5, 4000)
 dist_3 = np.random.normal(45, 6, 500)
 
 multimodal_dist = np.concatenate((dist_1, dist_2, dist_3), axis=0)

让我们把一维的数据分布形象化。

 import matplotlib.pyplot as plt
 import seaborn as sns
 sns.set_style('whitegrid')
 
 plt.hist(multimodal_dist, bins=50, alpha=0.5)
 plt.show()

使用高斯混合模型拆分多模态分布

下面我们将通过使用高斯混合模型计算每个分布的均值和标准差，将多模态分布分离回三个原始分布。高斯混合模型是一种可用于数据聚类的概率无监督模型。它使用期望最大化算法估计密度区域。

 from sklearn.mixture import GaussianMixture
 
 gmm = GaussianMixture(n_components=3)
 gmm.fit(multimodal_dist.reshape(-1, 1))
 
 means = gmm.means_
 
 # Conver covariance into Standard Deviation
 standard_deviations = gmm.covariances_**0.5  
 
 # Useful when plotting the distributions later
 weights = gmm.weights_  
 
 
 print(f"Means: {means}, Standard Deviations: {standard_deviations}")
 
 #Means: [29.4, 10.0, 38.9], Standard Deviations: [4.6, 3.1, 7.9]

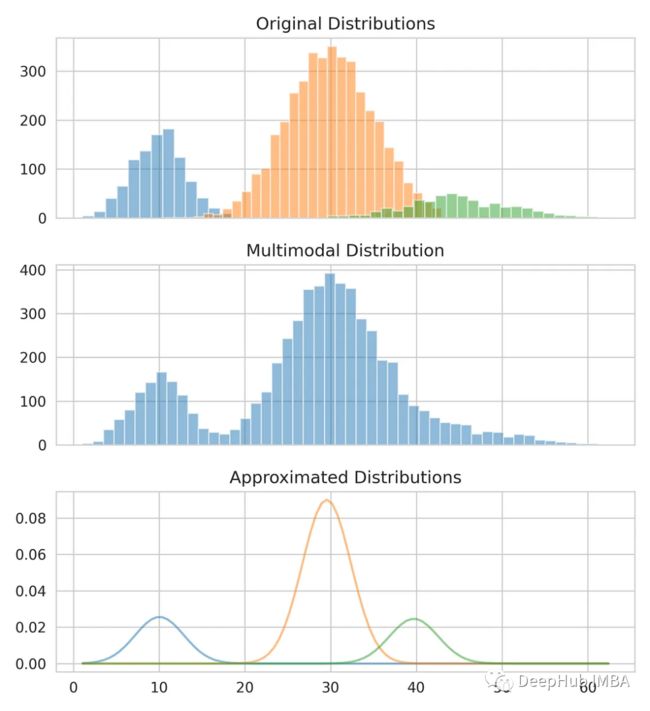
我们已经得到了均值和标准差，可以对原始分布进行建模。可以看到虽然平均值和标准差可能不完全正确，但它们提供了一个接近的估计。

把我们的估计和原始数据比较一下。

 from scipy.stats import norm
 
 fig, axes = plt.subplots(nrows=3, ncols=1, sharex='col', figsize=(6.4, 7))
 
 for bins, dist in zip([14, 34, 26], [dist_1, dist_2, dist_3]):
     axes[0].hist(dist, bins=bins, alpha=0.5)
     
 axes[1].hist(multimodal_dist, bins=50, alpha=0.5)
 
 x = np.linspace(min(multimodal_dist), max(multimodal_dist), 100)
 
 for mean, covariance, weight in zip(means, standard_deviations, weights):
     pdf = weight*norm.pdf(x, mean, std)
     plt.plot(x.reshape(-1, 1), pdf.reshape(-1, 1), alpha=0.5)
 
 plt.show()

总结

高斯混合模型是一个强大的工具，可以用来对复杂的数据分布进行建模和分析，同时也是许多机器学习算法的基础之一。它的应用范围涵盖了多个领域，能够解决各种数据建模和分析的问题。

这种方法可以作为一种特征工程技术来估计输入变量内子分布的置信区间。

https://avoid.overfit.cn/post/2d68eddf58c04732a4826c6d6c2d1a50

作者：Adrian Evensen