前缀、中缀和后缀表达式详解，中缀表达式到后缀表达式的转换规则，以及后缀表达式的计算规则，附计算代码

1. 中缀、前缀和后缀表达式

1.1 中缀表达式

首先，中缀表达式的这个“缀”指运算符在两个操作数的位置。中缀表达式其实就是我们常用的算术表达式，比如 2 + 9 - (32 * (19 - 4) +14)，我们很容易就可以得到计算结果，但是对于计算机来说，它们就得对各个运算符进行优先级比较以及弹栈和入栈等操作，其实计算机对于前缀表达式和后缀表达式更容易理解。

1.2 前缀表达式

前缀表达式，也称波兰式，指运算符处于两个操作数的前面，比如 2 + 3，那么前缀表达式就是 + 2 3；对于复杂点的表达式，如 13 * ((3 + 8) * 4)，前缀表达式为 * 13 * + 3 8 4，后续分析怎么转换。

1.3 后缀表达式

也称逆波兰式，指运算符处于两操作数后面，比如 2 + 3，后缀表达式为 2 3 +；对于复杂点的表达式，如 13 * ((3 + 8) * 4)，后缀表达式为 13 3 8 + 4 * *，后续会讲怎么转换。

 

2. 中缀表达式到后缀表达式的转换规则

前面我们提到计算机易于理解前缀表达式和后缀表达式，但我们生活中或使用计算器时是中缀表达式，这也就意味着我们需要将中缀表达式转换为前缀或后缀表达式，从而实现计算器的高效计算。

中缀表达式转换为后缀表达式的规则如下：

1.创建运算符栈s1和操作数数组a2，然后扫描中缀表达式；

2.如果是操作数，直接放入数组a2；

3.如果是运算符，栈s1为空或栈顶符号为左括号，或者优先级比栈顶运算符高，则入栈结束该步骤；否则将s1栈顶运算符弹出放入操作数数组a2，
 然后重复该步骤3。

4.如果是左括号，直接压入运算符栈s1；如果是右括号，依次弹出s1的运算符放入s2，直至遇到左括号结束，并将左、右括号舍弃。

5.循环步骤2-4直至表达式扫描结束，将s1的剩余运算符依次弹出放入数组a2，数组a2就是后缀表达式。

以下演示一个较复杂中缀表达式 3 * (11 - 8) - 45 / ((98 - 60) / 10 + 6)  转换后缀表达式的流程，流程如下。

1. 先创建运算符栈s1,和操作数数组a2，然后索引指向中缀表达式的第一位；

2. 3是操作数，放入数组a2的第一个位置，得到a2 = {3}；

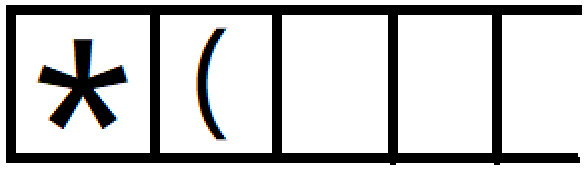
3. *是运算符，因为栈s1为空，*直接入栈s1，s1 = ；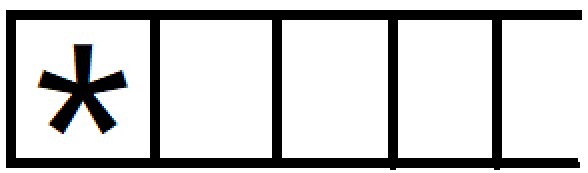

4. 遇到左括号，直接压入运算符栈s1，s1 = ；

5. 11是操作数，直接放入数组a2，得到a2 = {3, 11}；

6. - 是运算符，因为栈顶符号是左括号，- 直接入栈得到s1 =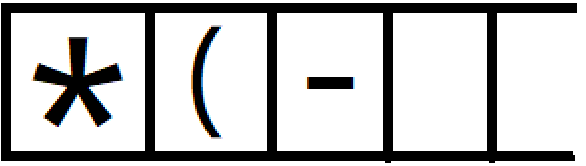 

7. 8是操作数，直接放入数组a2，得到a2 = {3, 11, 8}；

8. 遇到右括号，弹出s1中的运算符 - ，直到遇到左括号结束；此时a2={3, 11, 8, -}，s1 = 

9. - 是运算符，因为优先级低于栈顶符号 * ，将s1栈顶符号弹出放入数组a2，a2变为{3, 11, 8, -, *}，s1 = 

10. 重复步骤3，由于此时栈为空，则 - 直接入栈，s1 = 

11. 45是操作数，直接放入数组a2，得到a2 = {3, 11, 8, -, *, 45}；

12. / 是运算符，而且运算优先级高于s1的栈顶符号 -，所以直接入栈，s1 = 

13. 遇到左括号，直接压入运算符栈s1，s1 = ；

14. 遇到左括号，直接压入运算符栈s1，s1 = ；

15. 98是操作数，直接放入数组a2，得到a2 = {3, 11, 8, -, *, 45, 98}；

16. - 是运算符，因为栈顶符号是左括号，- 直接入栈,得到s1 = 

17. 60是操作数，直接放入数组a2，得到a2 = {3, 11, 8, -, *, 45, 98, 60}；

18. 遇到右括号，弹出s1中的运算符 - ，直到遇到左括号结束；此时a2={3, 11, 8, -, *, 45, 98, 60, -}，s1 = 

19. / 是运算符，而且栈顶符号是左括号，/ 直接入栈，得到s1 = 

20. 10是操作数，直接放入数组a2，得到a2 = {3, 11, 8, -, *, 45, 98, 60, -, 10}；

21. + 是运算符，因为优先级低于栈顶符号 / ，将s1栈顶符号 / 弹出放入数组a2，a2变为{3, 11, 8, -, *, 45, 98, 60, -, 10, /}，

      s1 = 

22. + 运算符接着和栈顶符号比较，此时由于栈顶符号是左括号，直接入栈，s1 =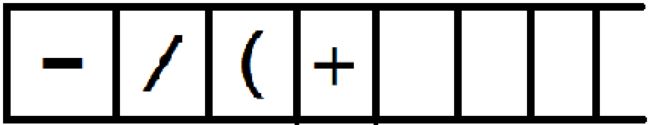 

23. 6是操作数，直接放入数组a2，得到a2 = {3, 11, 8, -, *, 45, 98, 60, -, 10, /, 6}；

24. 遇到右括号，弹出s1中的运算符 + ，直到遇到左括号结束；此时a2={3, 11, 8, -, *, 45, 98, 60, -, 10, /, 6, +}，

     s1 = 

25. 扫描结束，弹出s1中剩余运算符至数组a2，得到a2 = {3, 11, 8, -, *, 45, 98, 60, -, 10, /, 6, +, /, -}

因此，最终得到的后缀表达式为 3 11 8 - * 45 98 60 - 10 / 6 + / -

 

代码如下

static int priority(char c1){
        if((c1 == '*') || (c1 == '/')){
            return 2;
        }else{
            return 1;
        }
}

static List infixToPostfix(String infixExpress){
        char c;
        Stack s1 = new Stack();
        List a2 = new ArrayList();
        for (int i = 0; i < infixExpress.length(); i++) {
            c = infixExpress.charAt(i);
            if((c == '*') || (c == '/') || (c == '+') || (c == '-')){
                //如果栈空、栈顶元素是左括号，或者运算符优先级高于栈顶元素优先级，则入栈
                if((s1.isEmpty()) || ((char)s1.lastElement() == '(') || 
                    (priority(c) > priority((char)s1.lastElement()))){
                    s1.push(c);
                }else{
                    a2.add(String.valueOf(s1.pop()));
                    //循环比较，直至运算符可以入栈，结束；否则一直将栈顶元素弹出放入数组a2
                    while(!(s1.isEmpty() || ((char)s1.lastElement() == '(') || 
                        (priority(c) > priority((char)s1.lastElement())))){
                        a2.add(String.valueOf(s1.pop()));
                    }
                    s1.push(c);
                }
            }else if(c == '('){
                s1.push(c);
            }else if(c == ')'){
                char c2 = (char)s1.pop();
                //循环比较，直至匹配到左括号结束；否则一直将栈顶元素弹出放入数组a2
                while(c2 != '('){
                    a2.add(String.valueOf(c2));
                    c2 = (char)s1.pop();
                }
            }else if((c >= 48) && (c <= 57)){
                //如果是最后一位，那么直接将数字放入数组a2，结束
                if(i == infixExpress.length()-1){
                    a2.add(String.valueOf(c));
                }else{
                    String s2 = "" + c;
                    int cnt = 1;
                    char c3 = infixExpress.charAt(i+cnt);
                    while((c3 >= 48) && (c3 <= 57)){
                        s2 += c3;
                        cnt++;
                        //一直扫描数字，直至中缀表达式末尾，结束
                        if(i+cnt < infixExpress.length()){
                            c3 = infixExpress.charAt(i+cnt);
                        }else{
                            break;
                        }
                    }
                    i += (cnt-1);
                    a2.add(s2);
                }
            }else{
                //如果字符是空格或者表达式最后一个字符是 = ，不操作，否则表达式异常
                if(((i == infixExpress.length()-1) && (c == '=')) || (c == ' ')){
                }else{
                    System.out.println("Express is fault");
                }
            }
        }
        //最后需要将s1剩余的运算符弹出，放入数组a2中。
        while(! s1.isEmpty()){
            a2.add(String.valueOf(s1.pop()));
        }
        return a2;
    }

 

3. 后缀表达式的计算原则

我们得到后缀表达式 3 11 8 - * 45 98 60 - 10 / 6 + / -，那么怎么计算呢？其实，后缀表达式计算原则很简单，主要分为三步，如下

1. 创建一个栈，并且从左至右扫描表达式；

2. 遇到数字，将数字压入栈中；遇到运算符则弹出栈顶的两个元素，使用运算符进行计算，然后将计算结果再压入栈中；

3. 重复步骤2直到表达式扫描结束，最后弹出栈顶元素就是计算结果。

 

以上示例后缀表达式的计算步骤如下：

1. 创建栈stack，扫描表达式，将数字3, 11, 8依次压入栈stack，得到stack = 

2. 遇到运算符 - ，栈stack弹出 8 和 11，计算 11 - 8 得到3，入栈得到stack = 

3. 遇到运算符 * ，栈stack弹出 3 和 3，计算得到 9，入栈得到stack = 

4. 将数字45, 98, 60压入栈，得到stack = 

5. 遇到运算符 - ，栈stack弹出 60 和 98，计算 98- 60得到38，入栈得到stack = 

6. 将数字10压入栈，得到stack = 

7. 遇到运算符 / ，栈stack弹出 10 和 38，计算 38 / 10得到3 (java整数相除得到整数3，其它变成语言可得到3.8)，入栈得到

    stack = 

8. 将数字6压入栈，得到stack = 

9. 遇到运算符 + ，栈stack弹出 6 和 3，计算 3 + 6 得到9，入栈得到stack = 

10. 遇到运算符 / ，栈stack弹出 9 和 45，计算 45 / 9 得到5，入栈得到stack = 

11. 遇到运算符 - ，栈stack弹出 5 和 9，计算 9 - 5 得到4，入栈得到stack = 

12. 计算结束，弹出栈顶元素 4，所以计算结果为4.

 

代码如下

static String calculate(List ls){
        Stack st_result = new Stack();
        for (String s:ls) {
            // 因为这个计算后缀表达式的方法是和中缀表达式转后缀表达式联合使用的，而且中缀表达式
            // 转换后缀表达式的方法中考虑了运算符异常等异常，所以以下代码不考虑异常情况
            if(("-".equals(s)) || ("+".equals(s)) || ("*".equals(s)) || ("/".equals(s))){
                 int num_back = Integer.valueOf(st_result.pop());
                 int num_front = Integer.valueOf(st_result.pop());
                 switch(s){
                     case "-":
                         st_result.push((num_front - num_back) + "");
                         break;
                     case "/":
                         st_result.push((num_front / num_back) + "");
                         break;
                     case "+":
                         st_result.push((num_front + num_back) + "");
                         break;
                     case "*":
                         st_result.push((num_front * num_back) + "");
                         break;
                 }
            }else {
                st_result.push(s);
            }
        }
        return st_result.pop();
    }

 

 

完整测试代码以运行结果如下

static int priority(char c1){
        if((c1 == '*') || (c1 == '/')){
            return 2;
        }else{
            return 1;
        }
    }
    static List infixToPostfix(String infixExpress){
        char c;
        Stack s1 = new Stack();
        List a2 = new ArrayList();
        for (int i = 0; i < infixExpress.length(); i++) {
            c = infixExpress.charAt(i);
            if((c == '*') || (c == '/') || (c == '+') || (c == '-')){
                //如果栈空、栈顶元素是左括号，或者运算符优先级高于栈顶元素优先级，则入栈
                if((s1.isEmpty()) || ((char)s1.lastElement() == '(') || 
                    (priority(c) > priority((char)s1.lastElement()))){
                    s1.push(c);
                }else{
                    a2.add(String.valueOf(s1.pop()));
                    //循环比较，直至运算符可以入栈，结束；否则一直将栈顶元素弹出放入数组a2
                    while(!(s1.isEmpty() || ((char)s1.lastElement() == '(') || 
                            (priority(c) > priority((char)s1.lastElement())))){
                        a2.add(String.valueOf(s1.pop()));
                    }
                    s1.push(c);
                }
            }else if(c == '('){
                s1.push(c);
            }else if(c == ')'){
                char c2 = (char)s1.pop();
                //循环比较，直至匹配到左括号结束；否则一直将栈顶元素弹出放入数组a2
                while(c2 != '('){
                    a2.add(String.valueOf(c2));
                    c2 = (char)s1.pop();
                }
            }else if((c >= 48) && (c <= 57)){
                //如果是最后一位，那么直接将数字放入数组a2，结束
                if(i == infixExpress.length()-1){
                    a2.add(String.valueOf(c));
                }else{
                    String s2 = "" + c;
                    int cnt = 1;
                    char c3 = infixExpress.charAt(i+cnt);
                    while((c3 >= 48) && (c3 <= 57)){
                        s2 += c3;
                        cnt++;
                        //一直扫描数字，直至中缀表达式末尾，结束
                        if(i+cnt < infixExpress.length()){
                            c3 = infixExpress.charAt(i+cnt);
                        }else{
                            break;
                        }
                    }
                    i += (cnt-1);
                    a2.add(s2);
                }
            }else{
                //如果字符是空格或者表达式最后一个字符是 = ，不操作，否则表达式异常
                if(((i == infixExpress.length()-1) && (c == '=')) || (c == ' ')){
                }else{
                    System.out.println("Express is fault");
                }
            }
        }
        //最后需要将s1剩余的运算符弹出，放入数组a2中。
        while(! s1.isEmpty()){
            a2.add(String.valueOf(s1.pop()));
        }
        return a2;
    }

    static String calculate(List ls){
        Stack st_result = new Stack();
        for (String s:ls) {
            // 因为这个计算后缀表达式的方法是和中缀表达式转后缀表达式联合使用的，而且中缀表达式
            // 转换后缀表达式的方法中考虑了运算符异常等异常，所以以下代码不考虑异常情况
            if(("-".equals(s)) || ("+".equals(s)) || ("*".equals(s)) || ("/".equals(s))){
                 int num_back = Integer.valueOf(st_result.pop());
                 int num_front = Integer.valueOf(st_result.pop());
                 switch(s){
                     case "-":
                         st_result.push((num_front - num_back) + "");
                         break;
                     case "/":
                         st_result.push((num_front / num_back) + "");
                         break;
                     case "+":
                         st_result.push((num_front + num_back) + "");
                         break;
                     case "*":
                         st_result.push((num_front * num_back) + "");
                         break;
                 }
            }else {
                st_result.push(s);
            }
        }
        return st_result.pop();
    }
    public static void main(String[] args) {
        String s = "3 * (11 - 8) - 45 / ((98 - 60) / 10 + 6)";
        List posefixList = infixToPostfix(s);
        System.out.print("后缀表达式为：");
        for (Object o:posefixList) {
            System.out.print(o + " ");
        }
        System.out.println("\n后缀表达式计算结果是 " + calculate(posefixList));
    }