最短通路——迪克斯特拉算法
迪克斯特拉算法初探——图解算法
迪克斯特拉算法的大致思想是这样:求出起始顶点到各个后继顶点的最短通路,直到所求顶点为止。
由于直接从抽象的代码分析比较复杂(笔者很菜 零零碎碎花了好几天才搞懂),我们可从实际的例子
来感受该算法的思想,这样也符合由一般到抽象的认知过程(突然哲学)
首先来看一个直观的例子吧(看图说话)
标号是核心(L(v)实际上就是点v到a的某条通路的长度(为什么不说是最短路长度呢 ? 这个我后面会提到))
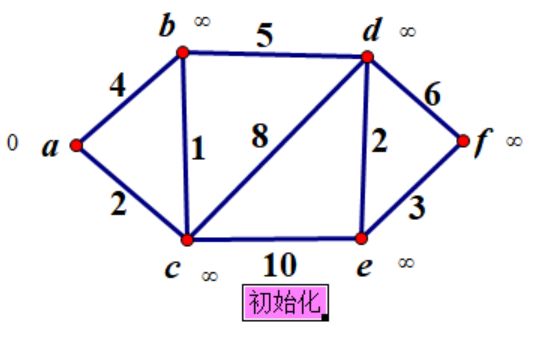
1.首先初始化标记 即:把a标号为0;其余点标号为无穷;
2.再定义一个空集S。
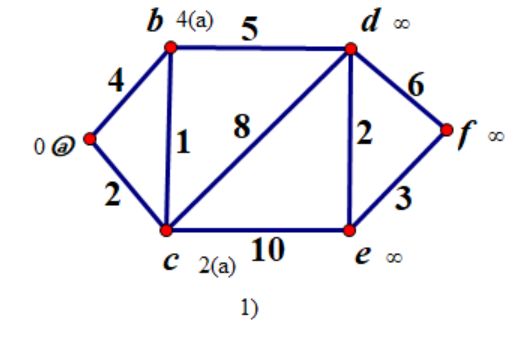
step 1:
看看图中发生了什么变化?
1.我们将标号最小的a(L(a)=0)纳入集合S中(图中用圈圈出); 即 S={a}
2.更新所有不属于S的顶点的标记 具体就是对不在集合S中的点v,其标号为min{ L(a)+w(a,v), L(v) } L(b)=4; L(c)=2;
显然 我们只能更新那些与a相邻的元素的标记。 # a-v之间如果不连通则w(a,v)=∞
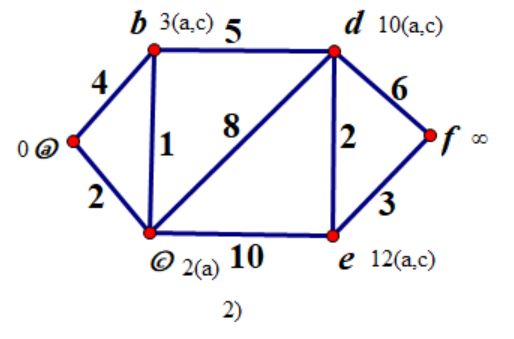
step 2:
这下 上次的标号就派上用场了呢:
我们把不在S中的顶点标号最小的顶点纳入到集合S中,即 c 得到 S={a,c};
对所有不属于S的顶点v,更新它们的标号 具体做法 L(v)= min{ L(c)+w(c,v), L(v) } L( b)=3;L(d)=10;L(e)=12;
注意:已经更新过的元素也可能会再次改变~b就是如此
标号再次改变说明存在更短的路径
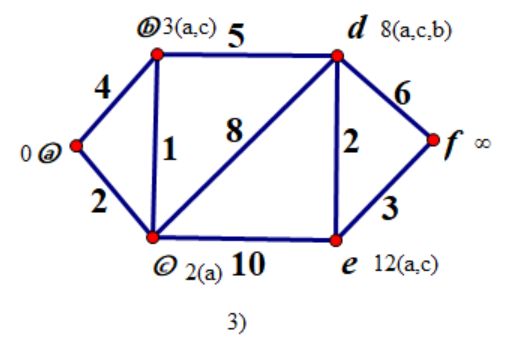
step 3:
这次L(b)为最小标号 所以把b添加到集合S中 S={a,c,b} # 至此 b加入到集合S中,所求的标号L(b)才是最短路的长度!
更新标号(以新加入S的顶点b为基准): L(v)= min{ L(b)+w(b,v), L(v) } L(d)=8;
大家发现没有,这个算法的简化之处在于,寻找新的点不需要求S中所有点和不在S中所有点的标号,
也就是说,只需要更新所有与新加入点相邻的点的标号,这一点需要慢慢体会,我就是卡在这儿出不去!
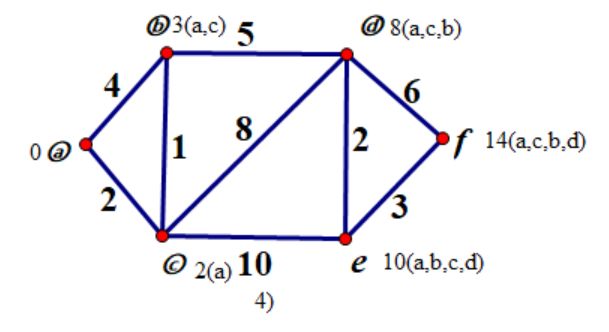
step 4:
step 5:
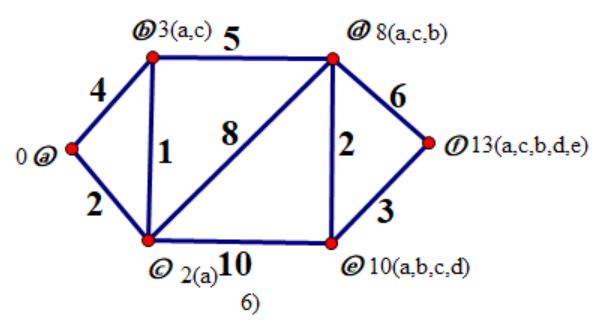
step 6 :
下面上点理论知识应该就可以接受了吧:
迪克斯特拉算法如下进行:求出a到第一个顶点的最短通路的长度,从a到第二个顶点的最短通路的长度,依次类推,直到求除从a到z的最短通路的长度为止。还有一个便利之处是,很容易扩展这个算法,求出从a到不只是z的所有顶点的最短通路的长度。
这个算法依赖于一系列的迭代。通过在每次迭代中添加一个顶点来构造特殊顶点的集合。在每次迭代中完成以个标记过程。在这个标记过程中,用只包含特殊顶点集合中的顶点的从a到w的最短通路来标记w.添加到特殊顶点中的顶点是尚在集合之外的那些顶点中带有最小标记的顶点。
首先用0标记a而用∞标记其余顶点。用记号L0(a)=0和L0(v)=∞来表示在没有发生任何迭代之前的这些标记(下标0表示“第0次”迭代)。这些标记是从a到这些顶点的最短通路的长度,其中这些通路只包含顶点a.(因为不存在a到其他顶点的这种通路,所以∞是a与这样的顶点之间的最短通路的长度。)
迪克斯特拉算法是通过形成特殊顶点的结合来进行的。设Sk表示在标记过程k次迭代之后的特殊顶点集。首先令S0=Ø。集合Sk通过把不属于Sk-1的带最小标记的顶点u添加到Sk-1形成的。
一旦把u添加到Sk中,就更新所有不属于Sk的顶点的标记,使得顶点v在第k个阶段的标记Lk(v)是只包含Sk中顶点(Sk+u)的从a到v的最短通路的长度。注意:在每一步中选择添加到Sk中的顶点u都是一个最优选择,使之成为贪婪算法(并且是最优解)。
设v是不属于Sk中的顶点。更新v的标记,注意Lk(v)是只包含Sk中顶点的从a到v的最短通路的长度。
注意:只包含Sk中顶点的最短通路,要么是只包含Sk-1中顶点的从a到v的最短通路,要么是在第k-1个阶段加上变{u,v}的从a到u的最短通路。 即 Lk(a,v)=min{Lk-1(a,v),Lk-1(a,u)+w(u,v)} w(u,v)为边的长度(权)
下面给出算法的伪代码:
procedure Dijkstra(G:所有权为正数的带权连通简单图)
{G所有顶点a=v0,v1,v2,……vn=z和权w(vi,vj), 若vi,vj无边则权w(vi,vj)为∞}
for i:=1 to n
L(vi):=∞
L(a):=0
S:=Ø
{现在初始化标记,使得a的标记为0 而所有其余标记为∞,S是空集}
while z∉S
u := a∉S的L(u)最小的一个顶点
S := S U {u}
for 所有不属于S的L(u)最小的一个顶点
if L(u)+w(u,v)
我们现在回过头来看这个算法,其实有两条线:
一条线是集合,这个集合中每次新添加一个顶点元素(这个顶点其实就是在集合S外 距离a最短的顶点!)直到所求的顶点纳入这个集合为止 (这个是算法停止的标志)
另一条线是标号,每次循环改变其余顶点的标号,标号就是该顶点到起始顶点的某通路的长度!不过,需要注意的是: 只有当该顶点包含到集合里面时,标号才代表最短通路的长度!
他们之间是怎么联系的呢,不难发现 我们把标号作为寻找集合S外到a最近的顶点的量度,而集合S提供了计算标号的划分范围!
实际上,正是这种标号的引入降低了计算的复杂度,使其从O(n^3)-->O(n^2)
至此 ,算法的思路也就明朗了!
具体实现的话后期更新给出,离散好迷~
参考书目:《离散数学及其应用》