一种新颖的PMSM转子初始位置检测

前言：PMSM常见的初始位置检测方法，以六脉冲最为知名。即使SPM，利用饱和效应仍然可以实现初始位置的检测，误差稍大，大约30°以内。

复杂一点的就是连续方波注入或者脉振注入，需要PI调节器或者各种滤波器，工程实现复杂。传统脉振比较常见就不展开了，高频方波注入之前的文章已经讲过了，这两种方法都能适用于SPM，利用饱和凸极实现位置的估算。

简介：本文基于传统脉振高频注入，提出了一种虚拟坐标系下的脉振注入方法，省略了带通滤波器、低通滤波器和锁相环，并且不需要特殊位置错误收敛的判断。

控制方法

同步旋转坐标系下，向直轴注入余弦高频信号，电压方程如下：
$$\left[\begin{array}{c}{u}_{dh}\\ u_{qh}\end{array}\right]=u_{inj}\left[\begin{array}{c}\cos {\omega }_{i}t\\ 0\end{array}\right]$$

$t$ 为时间， ${\omega }_i$ 是注入信号频率， $u_{inj}$ 是注入余弦信号的幅值。

在瞬态下，通过对高频电流信号的解耦，经过低通滤波器和带通滤波器的处理，结合锁相环可以输出角度和速度。

传统脉振控制框图如下：

图1 传统脉振注入控制框图

在 $\Delta \theta =0$ , $\Delta \theta =\pi /2$ , $\Delta \theta =3\pi /2$ , $\Delta \theta =\pi$ ,有可能辨识角度会错误的收敛，造成辨识出现较大误差，必须对错误收敛的情况进行判断。

在传统脉振的基础上，提出了基于虚拟旋转坐标系的脉振注入。在转子静止时，虚拟出一个以较高速度 ${\omega }_r^{\ast }$ 旋转的坐标系。如下图所示，虚线表示虚拟旋转坐标系，实线表示实际旋转坐标系。

图2 虚拟坐标系和同步旋转坐标系

当虚拟坐标系的 $d^{\ast }$ 轴注入余弦电压 $U_{c}cos({\omega }_{c}t)$ ,通过角度差将注入电压转换到实际旋转坐标系。采样三相电流后，经过坐标变换得到虚拟坐标系的交、直轴电流 $i_d^{\ast }$ 和 $i_q^{\ast }$。对电流进行滤波和耦合处理，再对滤波结果作反正切，得到转子位置。

假设电机静止，虚拟坐标系的旋转速度和注入的高频余弦信号速度远大于电机实际速度。虚拟坐标系和真实旋转坐标系的角度差为： $\Delta \theta ={\omega }_r^{\ast }t-\theta$

同步电机的电压方程如下：

$\left[\begin{array}{c}{u}_d\\ u_q\end{array}\right]=\left[\begin{array}{cc}{R}_s+L_{d}p& -{\omega }_r{L}_q\\ {\omega }_r{L}_d& R_s+L_{q}p\end{array}\right]\left[\begin{array}{c}{i}_d\\ i_q\end{array}\right]+\left[\begin{array}{c}0\\ {\psi }_r{\omega }_r\end{array}\right]$

向虚拟旋转坐标系注入高频余弦信号，频率为 ${\omega }_c$
：

$\left[\begin{array}{c}{u}_d^{\ast }\\ u_q^{\ast }\end{array}\right]=\left[\begin{array}{c}{U}_c\cos {\omega }_{c}t\\ 0\end{array}\right]$

经过坐标变换，把虚拟旋转坐标系下电压转换到真实旋转坐标系下：

$\left[\begin{array}{c}{u}_d\\ u_q\end{array}\right]=U_{c}cos({\omega }_{c}t)\left[\begin{array}{c}cos({\omega }_r^{\ast }t-\theta )\\ sin({\omega }_r^{\ast }t-\theta )\end{array}\right]$

代入真实旋转坐标系的电压方程，得到响应电流：

$\left[\begin{array}{c}{i}_d\\ i_q\end{array}\right]={\psi }^{-1}{U}_{c}cos({\omega }_{c}t)\left[\begin{array}{c}cos({\omega }_r^{\ast }t-\theta )\\ sin({\omega }_r^{\ast }t-\theta )\end{array}\right]$

$\psi =\left[\begin{array}{cc}{R}_s+L_{d}p& -{\omega }_r{L}_q\\ {\omega }_r{L}_d& R_s+L_{q}p\end{array}\right]$

将 $i_d$ 和 $i_q$ 变换到虚拟坐标系得到 $i_d^{\ast }$ 和 $i_q^{\ast }$ ,即

$\left[\begin{array}{c}{i}_d^{\ast }\\ i_q^{\ast }\end{array}\right]={\xi }^{-1}{\psi }^{-1}{U}_{c}cos({\omega }_{c}t)\left[\begin{array}{c}cos({\omega }_r^{\ast }t-\theta )\\ sin({\omega }_r^{\ast }t-\theta )\end{array}\right]$

$\xi =\left[\begin{array}{cc}cos({\omega }_r^{\ast }t-\theta )& -sin({\omega }_r^{\ast }t-\theta )\\ sin({\omega }_r^{\ast }t-\theta )& cos({\omega }_r^{\ast }t-\theta )\end{array}\right]$

电机静止状态下，虚拟坐标系相对电机有较大速度，所以有

${\psi }^{\ast }=\left[\begin{array}{cc}{R}_s+L_{d}p& -{\omega }_r^{\ast }{L}_q\\ {\omega }_r^{\ast }{L}_d& R_s+L_{q}p\end{array}\right]$

将 $i_d^{\ast }$ 和 $i_q^{\ast }$ 都与 $cos({\omega }_{c}t)cos(2{\omega }_r^{\ast }t)$ 相乘，并经过低通滤波得到：

$\left[\begin{array}{c}{i}_d^{{}^{\prime }}\\ i_q^{{}^{\prime }}\end{array}\right]=\frac{pq{U}_c}{8}\left[\begin{array}{c}cos(2\theta -\sigma )\\ sin(2\theta -\sigma )\end{array}\right]$

$i_d^{{}^{\prime }}$ 和 $i_q^{{}^{\prime }}$ 分别为经过滤波后的虚拟坐标系交直轴电流。 $\sigma$ 为偏置角度。

$\sigma =arctan(\frac{{\omega }_r^{\ast }}{{\omega }_r^{\ast }+{\omega }_c})$

对电流求反正切得到

$\theta =\frac{1}{2}arctan\frac{i_q^{\ast }}{i_d^{\ast }}+\frac{1}{2}\sigma$

辨识出初步角度后，再根据饱和效应来检测N-S磁极。

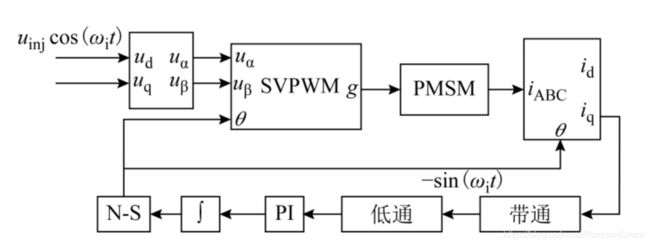
采用虚拟旋转坐标系的脉振注入，可以省略带通滤波器和锁相环，有效检测转子位置，并且不需要错误收敛的预判。控制框图如下：

图3 虚拟坐标系脉振注入控制框图

仿真波形

图4 仿真整体框图

电机参数：

图5 仿真使用的电机参数

设置初始角度0°，角度收敛过程如下，其中上图为误差，不超过10°，下图与实际初始位置和辨识位置。

图6 初始位置0°的辨识过程

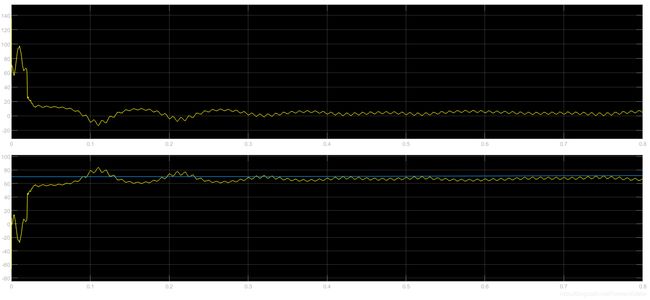
设置初始角度70°，角度收敛过程如下：

图7 初始位置70°的辨识过程

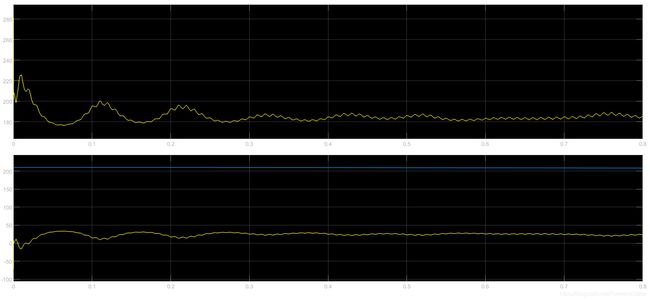
设置初始角度150°，角度收敛过程如下。磁极反了，最后需要辨识磁极，抛开磁极辨识误差最大大约6°。

图8 初始位置150°的辨识过程

设置初始角度210°，角度收敛过程如下。磁极反了，最后需要辨识磁极，抛开磁极辨识误差最大大约8°。

图9 初始位置210°的辨识过程

设置初始角度300°，角度收敛过程如下：

图10 初始位置300°的辨识过程

辨识过程中的三相电流：

图11 辨识过程中三相电流

总体误差：

总结：

虚拟注入是一种比较新颖的方法，去掉了PLL和带通滤波器，计算量减小了许多，有兴趣的朋友可以实际尝试一下。

注入电压频率我选择的250Hz，虚拟旋转频率选择了50Hz。这种方法目前看，因为只能计算出角度，如果通过角度微分计算速度会有较大误差和噪声，所以不推荐用于低速的控制。

参考文献就不贴出来了，论文相互借鉴，还有不少的错误。

作者简介：

我是转子磁场定向，十余年电控产品开发经验，精通永磁同步电机和三相异步电机无感FOC控制，可提供项目开发和技术咨询，有意加PMSM_RFO