永磁同步电机转子位置估算专题 —— 基波模型与转子位置角
前言
永磁同步电机转子位置估算专题将作为一个系列来写,将永磁同步电机常用的电机位置估算法方法分解为若干子类,再逐个写具体原理。文章风格与其他文章一致,保持通俗易懂,又不失深度。
本篇为该专题的一个开题之作,先理解转子位置角指的什么角,并和数学模型联系起来。
文章目录
-
- 前言
- 一、永磁同步电机的转子位置角
- 二、转子位置角在哪里反应
-
- 2.1 α β \alpha \beta αβ坐标系下的数学模型
- 2.2 α β \alpha \beta αβ轴的转子磁链分量包含位置信息
- 2.3 α β \alpha \beta αβ轴的反电势电压分量包含位置信息
- 三、小结
一、永磁同步电机的转子位置角
本文想要讲明白如何估算转子位置角,这是一个比较大的话题,为了把这个问题说透彻,首先要搞明白什么是转子位置角。
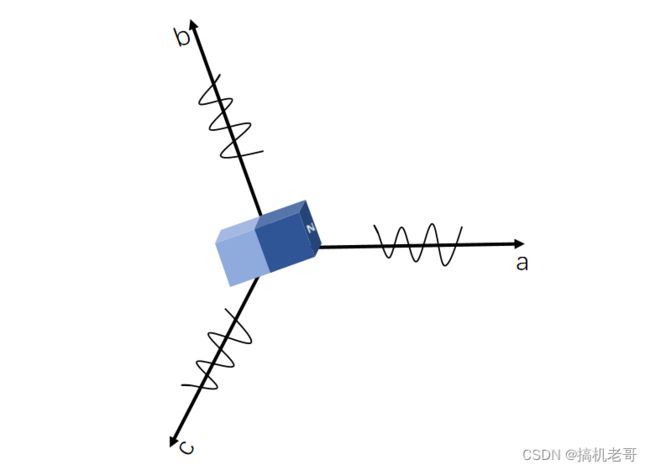
先补充一下永磁同步电机的基础知识,在做永磁同步电机控制时,我们关注的是定子与转子之间的相互作用力,这个力是定子磁场和转子磁场相互作用产生的。其中永磁同步电机的转子为一块永磁体,被生产出来后,其磁场大小就是固定的,其方向为转子N极指向的方向。定子磁场由电流产生,电流越大,产生的磁场越强,每一相电流产生的磁场大小都正比于当前时刻的电流,方向为该相在空间上的方向。总的定子磁场即三相电流产生的磁场的矢量和。
以一对极的永磁同步电机为例,其简化模型如上图。
为了说明转子位置角在空间上的关系,此处分析使用预定位法把转子拖到0°的过程。
令 i d = 10 A , i q = 0 , f o c A n g l e = 0 ; id = 10A,iq = 0,focAngle = 0; id=10A,iq=0,focAngle=0;
进行反park变换及反clark变换
[ i α i β ] = [ c o s θ s i n θ − s i n θ c o s θ ] [ i d i q ] (1) \left[\begin{array}{c} i_{\alpha }\\ i_{\beta } \end{array}\right] = \left[\begin{array}{c} cos\theta&sin\theta\\ -sin\theta & cos\theta \end{array}\right] \left[\begin{array}{c} i_{d }\\ i_{q } \end{array}\right] \tag{1} [iαiβ]=[cosθ−sinθsinθcosθ][idiq](1)
反park变换
[ i a i b i c ] = 2 3 [ 1 0 − 1 2 3 2 − 1 2 − 3 2 ] [ i α i β ] (2) \left[\begin{array}{c} i_{a}\\ i_{b} \\ i{c} \end{array}\right] = \frac{2}{3} \left[\begin{array}{c} 1 & 0\\ -\frac{1}{2} & \frac{\sqrt3}{2} \\ -\frac{1}{2} & -\frac{\sqrt3}{2} \end{array}\right] \left[\begin{array}{c} i_{\alpha }\\ i_{\beta } \end{array}\right] \tag{2} ⎣⎡iaibic⎦⎤=32⎣⎢⎡1−21−21023−23⎦⎥⎤[iαiβ](2)
反clark变换
带入 令 i d = 10 A , i q = 0 , f o c A n g l e = 0 id = 10A,iq = 0,focAngle = 0 id=10A,iq=0,focAngle=0,有 i α = 10 A , i β = 0 ; i a = 6.67 A , i b = − 3.3 A , i c = − 3.3 A i_{\alpha} = 10A, i_{\beta} = 0; i_a = 6.67A,i_b = - 3.3A,i_c = -3.3A iα=10A,iβ=0;ia=6.67A,ib=−3.3A,ic=−3.3A
放到上图,矢量合成,无论在 α β \alpha \beta αβ坐标系,还是在 a b c abc abc坐标系,都可以得到同样的结论,合成矢量的方向和a轴重合,大小为10A;
所以当预定位转子位置角为0度时,得到一个方向和a轴重合的定子磁场,把转子拉到a轴方向。也可以说转子位置角为0度时,转子N极位置和a相定子线圈重合,到此,以下说法得到验证:转子位置角指的是在空间上转子N极与定子a相绕组的电气夹角。
此处的转子位置角,也叫矢量角,磁极位置角,不同行业有不同的习惯叫法。
二、转子位置角在哪里反应
要估算出转子位置,必须知道转子位置在不同位置的时候,会有什么样的反应。在abc坐标系,三相电压、电流、磁链,相互耦合,数学模型复杂,常见的转子位置估算方法在 α β \alpha \beta αβ坐标系下进行。
2.1 α β \alpha \beta αβ坐标系下的数学模型
先来看电压方程
[ v α v β ] = [ i α i β ] R s + d d t [ ϕ α ϕ β ] (3) \left[\begin{array}{c} v_{\alpha }\\ v_{\beta } \end{array}\right] = \left[\begin{array}{c} i_{\alpha }\\ i_{\beta } \end{array}\right] R_s + \frac{d}{dt} \left[\begin{array}{c} \phi_{\alpha }\\ \phi_{\beta } \end{array}\right] \tag{3} [vαvβ]=[iαiβ]Rs+dtd[ϕαϕβ](3)
其中 ϕ α ϕ β \phi_{\alpha} \phi_{\beta} ϕαϕβ表示 α β \alpha \beta αβ轴磁链
[ ϕ α ϕ β ] = [ c o s θ s i n θ − s i n θ c o s θ ] [ L s i d + ϕ f L s i q ] (4) \left[\begin{array}{c} \phi_{\alpha }\\ \phi_{\beta } \end{array}\right] = \left[\begin{array}{c} cos\theta&sin\theta\\ -sin\theta & cos\theta \end{array}\right] \left[\begin{array}{c} L_s i_{d } + \phi_f\\ L_s i_{q } \end{array}\right] \tag{4} [ϕαϕβ]=[cosθ−sinθsinθcosθ][Lsid+ϕfLsiq](4)
把 d q dq dq轴磁链变换到 α β \alpha \beta αβ轴
[ ϕ α ϕ β ] = [ i α i β ] L s + [ ϕ f c o s θ ϕ f s i n θ ] (5) \left[\begin{array}{c} \phi_{\alpha }\\ \phi_{\beta } \end{array}\right] = \left[\begin{array}{c} i_{\alpha }\\ i_{\beta } \end{array}\right]L_s+ \left[\begin{array}{c} \phi_{f }cos\theta\\ \phi_{f}sin\theta \end{array}\right] \tag{5} [ϕαϕβ]=[iαiβ]Ls+[ϕfcosθϕfsinθ](5)
其中 ϕ f \phi_f ϕf表示永磁体磁链。
相对于以上形式的电压方程,我想更多朋友更熟悉以下形式
[ v α v β ] = [ i α i β ] R s + d d t [ L s i α L s i β ] + [ − ω e ϕ f s i n θ ω e ϕ f c o s θ ] (6) \left[\begin{array}{c} v_{\alpha }\\ v_{\beta } \end{array}\right] = \left[\begin{array}{c} i_{\alpha }\\ i_{\beta } \end{array}\right] R_s + \frac{d}{dt} \left[\begin{array}{c}L_s i_{\alpha }\\L_s i_{\beta } \end{array}\right] + \left[\begin{array}{c}- \omega_e \phi_{f } sin\theta \\ \omega_e\phi_{f}cos\theta \end{array}\right] \tag{6} [vαvβ]=[iαiβ]Rs+dtd[LsiαLsiβ]+[−ωeϕfsinθωeϕfcosθ](6)
其中 ω e \omega_e ωe为电角速度。
但是相比较于(6),(4)和(5)更容易说明问题
2.2 α β \alpha \beta αβ轴的转子磁链分量包含位置信息
(4)中, α β \alpha \beta αβ轴的磁链由 d q dq dq轴磁链ipark变换得到,其中, d d d轴磁链由 L s i d L_s i_{d } Lsid 和 ϕ f \phi_f ϕf两部分组成,前面说了, d d d轴的的位置定义为永磁体 N N N极指向的方向,所以永磁体磁链 ϕ f \phi_f ϕf只存在于 d d d轴,另一部分为电流流经 d d d轴电感产生的定子磁链 L s i d L_s i_{d } Lsid ; q q q轴只有定子磁链 L s i q L_s i_{q } Lsiq。
将(4)中的ipark变换展开,得到式(5)
可以看到,**永磁同步电机气隙中的磁链由两部分组成,一部分为定子磁链 [ i α i β ] L s \left[\begin{array}{c} i_{\alpha }\\ i_{\beta } \end{array}\right]L_s [iαiβ]Ls,由电流流过定子线圈产生,另一部分为转子磁链 [ ϕ f c o s θ ϕ f s i n θ ] \left[\begin{array}{c} \phi_{f }cos\theta\\ \phi_{f}sin\theta \end{array}\right] [ϕfcosθϕfsinθ],由转子永磁体产生。
α β \alpha \beta αβ坐标系中的转子磁链分量包含转子角度信息。
2.3 α β \alpha \beta αβ轴的反电势电压分量包含位置信息
将(5)代入(3)得到(6),该式子为常见的 α β \alpha \beta αβ坐标系电压方程表达式。我们知道磁场变化产生电场,在永磁同步电机中,每一相定子线圈绕在定子铁芯形成封闭的空间,该空间内,磁链变化,在线圈两端形成电压,磁链变化越快,产生的电压越大。 [ − ω e ϕ f s i n θ ω e ϕ f c o s θ ] \left[\begin{array}{c}- \omega_e \phi_{f } sin\theta \\ \omega_e\phi_{f}cos\theta \end{array}\right] [−ωeϕfsinθωeϕfcosθ]描述了转子磁场旋转产生的电压,与转子转速及转子当前角度的关系,这部分电压也叫反电动势; [ L s i α L s i β ] \left[\begin{array}{c}L_s i_{\alpha }\\L_s i_{\beta } \end{array}\right] [LsiαLsiβ]描述了定子磁场变化产生的电压与电流的关系。
α β \alpha \beta αβ坐标系中的反电动势电压分量包含转子角度信息。
三、小结
本文为永磁同步电机转子位置估算专题的第一篇文章,为保证每篇文章篇幅不至于过长,在此收尾。后续文章把转子位置估算的常用方法分解为, α β \alpha \beta αβ坐标系下的基波模型位置估算、 d q dq dq坐标系下的基波模型位置估算、注入信号类的位置估算,等多个方向,具体分解。
喜欢我的文章,记得点个关注哦。