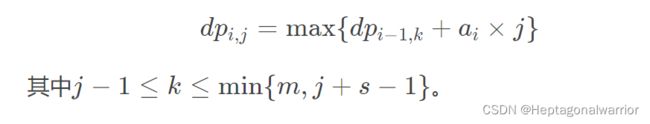第13期：动态规划-dp题集

1 P7972 [KSN2021] Self Permutation

---

//【动态规划1】动态规划的引入

---

2 P1216 [USACO1.5][IOI1994]数字三角形 Number Triangles

        定义状态(i,j)的指标函数d(i,j)为从格子(i,j)出发时能得到的最大和(包括格子(i,j)本身的值)。在这个状态定义下，原问题的解是d(1,1)。

        状态转移：从格子(i,j)出发有两种决策。如果往左走，则走到(i+1,j)后需要求“从(i+1,j)出发后能得到的最大和”这一问题，即d(i+1,j)。类似地，往右走之后需要求解d(i+1,j+1)。由于可以在这两个决策中自由选择，所以应选择d(i+1,j)和d(i+1,j+1)中较大的一个。

        状态转移方程：。

        如果连“从(i+1,j)出发走到底部”这部分的和都不是最大的，加上a(i,j)之后肯定也不是最大的。这个性质称为最优子结构（optimal substructure），也可以描述成“全局最优解包含局部最优解”。

#include
using namespace std;
int n,a[1005][1005],d[1005][1005];
inline int read(){
    char c=getchar();int x=0,f=1;
    while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();}
    while(c>='0'&&c<='9'){x=x*10+c-'0';c=getchar();}
    return x*f;
}
int solve(int i,int j){
    if(d[i][j]>=0) return d[i][j];    
    return d[i][j]=a[i][j]+(i==n?0:max(solve(i+1,j),solve(i+1,j+1)));
}
int main(){
    n=read();
    for(int i=1;i<=n;++i){
        for(int j=1;j<=i;++j){
            a[i][j]=read();
        }
    }
    memset(d,-1,sizeof(d));
    for(int j=1;j<=n;++j) d[n][j]=a[n][j];
    for(int i=n-1;i>=1;--i){
        for(int j=1;j<=i;++j){
            solve(i,j);
        }
    }
    printf("%d\n",d[1][1]);
    return 0;
}

#include 
#include 
using namespace std;

int r;
int s[1005][1005];
int main() {
    scanf("%d",&r);
    for (int i = 1;i <= r;i ++) {
        for (int j = 1;j <= i;j ++) {
            scanf("%d",&s[i][j]);
        }
    }
    for (int i = r - 1;i >= 1;i --) {
        for (int j = 1;j <= i;j ++) {
            s[i][j] += max(s[i + 1][j],s[i + 1][j + 1]);
        }
    }
    printf("%d",s[1][1]);
    return 0;
}

3 P1434 [SHOI2002]滑雪

深搜+记忆化搜索+dp

#include 
#define max(a,b) (a > b ? a : b)
#define N 120
int dx[] = {1,0,-1,0};
int dy[] = {0,-1,0,1};
int m[N][N];
int dp[N][N];
int ans = 1;
int r, c;
int in(int x,int y){
	if(x >= 0 && y >= 0 && x < r && y < c) return 1;
	else return 0;
}
int dfs(int x,int y){
	if(dp[x][y] > 1) return dp[x][y];
	for(int i = 0;i < 4;i ++){
		int tx = x + dx[i];
		int ty = y + dy[i];
		if(in(tx,ty) && m[tx][ty] < m[x][y]){
			dp[x][y] = max(dp[x][y],dfs(tx,ty)+1);
		}
	}
	return dp[x][y];
}
int read(){
    char c=getchar();int x=0,f=1;
    while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();}
    while(c>='0'&&c<='9'){x=x*10+c-'0';c=getchar();}
    return x*f;
}
int main(){
	int i, j;
	r=read();c=read(); 
	for(i = 0;i < r;i ++){
		for(j = 0;j < c;j ++){
			dp[i][j] = 1;
			m[i][j]=read();
		}
	}
	for(i = 0;i < r;i ++)
		for(j = 0;j < c;j ++)
			ans = max(ans,dfs(i,j));
	printf("%d\n",ans);
	return 0;
}

4 P2196 [NOIP1996 提高组] 挖地雷

①DP：定义状态f[i]为以第i个节点结束的最大值,则可以写出状态转移方程：

这样就不难写出代码来了.至于输出,用一个pre[i]数组存储i的前驱结点,递归输出即可.

#include
using namespace std;
int n,a[205],g[205][205],pre[205],f[205],t,ans;
void print(int x){
	if(pre[x]==0){
		cout<>n;
	for(int i=1;i<=n;i++) cin>>a[i];
	for(int i=1;i>x;
			if(x==1) g[i][j]=1;
		}
	}
	for(int i=1;i<=n;i++){
		for(int j=1;j<=n;j++){
			if(g[j][i]&&f[j]>f[i]){
				f[i]=f[j];
				pre[i]=j;
			}
		}
		f[i]+=a[i];
		if(f[i]>ans){
			ans=f[i];
			t=i;
		}
	}
	print(t);
	cout<

②dfs

#include
using namespace std;
bool f[21][21];//记录是否有路径相连
int a[21];//记录地雷数
int path[21],ans[21],cnt;//path记录路径，ans记录答案，cnt记录走了多少个点
bool b[21];//记录该点是否走过
int n;
int maxx;//记录挖的最大地雷数
bool chck(int x)//检查是否还能继续往下挖
{
	for(int i=1;i<=n;i++)
	{
		if(f[x][i]&&!b[i]) return false;
 	}
 	return true;
}
void dfs(int x,int stp,int sum)//x记录现在位置，stp记录走了几个点，sum记录挖的地雷数
{
	if(chck(x))
	{
		if(maxx>n;
	for(int i=1;i<=n;i++)
	cin>>a[i];
	for(int i=1;i>f[i][j];//这里是单向边，题目没说清楚
	}
	for(int i=1;i<=n;i++)
	{
		b[i]=1;
		path[1]=i;//记录起点
		dfs(i,1,a[i]);
		b[i]=0;
	}
	for(int i=1;i<=cnt;i++)
	cout<

 5 P4017 最大食物链计数(偏拓扑 图论)

#include
#define N 5005
#define M 500005
#define inf 0x3f3f3f3f
#define mod 80112002
#define endl '\n'
#define debug cerr<<__LINE__<'9') c=gc();
    while(c>='0'&&c<='9') k=(k<<3)+(k<<1)+(c^48),c=gc();
    return k;
}
inline int Add(const int x,const int y){return x+y>=mod?x+y-mod:x+y;}
inline void write(const int x){if(x>9) write(x/10);putchar((x%10)|48);}
inline int dfs(const int u){
    if(dp[u]) return dp[u];if(!out[u]) return 1;int ans=0;
    for(register int i=head[u];i;i=e[i].nxt) ans=Add(ans,dfs(e[i].to));
    return dp[u]=ans;
}
main(void){
    n=read();m=read();
    for(register int i=1;i<=m;i++) add(read(),read());
    for(register int i=1;i<=n;i++)
    if(!in[i]&&out[i]) ans=Add(ans,dfs(i));
    return write(ans),putchar('\n'),0;
}

#include
#ifdef ONLINE_JUDGE
	char buf[1<<21],*p1=buf,*p2=buf;
	#define getchar() (p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++)
#endif
int read()
{
	int a=0;char c;
	while((c=getchar())<'0');
	while(c>='0')a=a*10+(c^48),c=getchar();
	return a;
}
const int mod=80112002;
typedef struct{int to,next;}node;
node edge[500003];int head[5003];
int end[5003],_e,dp[5003],q[5003],_q,in[5003],out[5003];
int main()
{
	int n=read(),m=read(),i,x,Q,g,V;
	for(i=1;i<=m;i++)
	{
		edge[i].next=head[x=read()];
		in[edge[i].to=read()]++;
		head[x]=i;
		out[x]++;
	}
	for(i=1;i<=n;i++)
	{
		if(in[i]==0)q[++_q]=i,dp[i]=1;
		if(out[i]==0)end[++_e]=i;
	}
	for(i=1;i<=_q;i++)
	{
		Q=q[i];
		dp[Q]%=mod;
		for(g=head[Q];g;g=edge[g].next)
		{
			V=edge[g].to;
			dp[V]+=dp[Q];if(dp[V]>2000000000)dp[V]%=mod;
			if(--in[V]==0)q[++_q]=V;
		}
	}
	int ans=0;
	for(i=1;i<=_e;i++)
	{
		ans+=dp[end[i]];if(ans>=2000000000)ans%=mod;
	}
	printf("%d",ans%mod);
}

#include
using namespace std;
const int mod=80112002;
bool nHst[5050];
//false -> 食物链顶端
vectorEat[5050];
int dp[5050];
int n,m;
int ans;
int dfs(int now){
    if(!Eat[now].size()) return dp[now]=1;
    int res=0;
    for(int i=0;i>n>>m;
    int x,y;
    while(m--){
        scanf("%d%d",&x,&y);
        //y吃x
        Eat[y].push_back(x);
        nHst[x]=true;
    }
    for(int i=1;i<=n;i++) if(!nHst[i]) 
        ans=(ans+dfs(i))%mod;
    cout<

#include
    #define Re register//能少些一堆register
    #define Mod 80112002
    using namespace std;
    const int N=5005;
    int n,m,du[N],inu[N];
    int ans,sa[N];
    int head[N*100],cnt;
    struct ed{
        int to,nex;
    }edge[N*100];
    inline void add(int x,int y){
        cnt++;
        edge[cnt].to=y;
        edge[cnt].nex=head[x];
        head[x]=cnt;
    }
    void in(int &read){
        int x=0;char ch=getchar();
        while(ch<'0'||ch>'9')ch=getchar();
        while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
        read=x;
    }
    int dfs(int st){
        if(!du[st])return 1;
        if(sa[st])return sa[st];
        int sum=0;
        for(Re int i=head[st];i;i=edge[i].nex)
            sum=(sum+dfs(edge[i].to))%Mod;//每加一个数就%一次
        sa[st]=sum%Mod;
        return sa[st];
    }
    int main(){
        in(n);in(m);
        int a,b;
        for(Re int i=1;i<=m;i++){
            in(a);in(b);
            inu[b]++;du[a]++;
            add(a,b);
        }
        for(Re int i=1;i<=n;i++)
            if(!inu[i])ans=(ans+dfs(i))%Mod;
        printf("%d\n",ans);
        return 0;
}

6 P1048 [NOIP2005 普及组] 采药(01背包)

首先定义状态 dp[i][j] 以j为容量为放入前i个物品(按 i从小到大的顺序)的最大价值。

动态转移方程：

//二维dp
#include
using namespace std;
int w[105],val[105];
int dp[105][105]; 
int main(){
	int t,m,res=-1;
	cin>>t>>m;
	for(int i=1;i<=m;i++){
		cin>>w[i]>>val[i];
	}
	for(int i=1;i<=m;i++){
		for(int j=t;j>=0;j--){
			if(j>=w[i]){
				dp[i][j]=max(dp[i-1][j-w[i]]+val[i],dp[i-1][j]);
			}else{
				dp[i][j]=dp[i-1][j];
			}
		}
	}
	cout<

//一维dp
#include
using namespace std;
int w[105],val[105];
int dp[1005]; 
int main(){
	int t,m,res=-1;
	cin>>t>>m;
	for(int i=1;i<=m;i++){
		cin>>w[i]>>val[i];
	}
	for(int i=1;i<=m;i++){
		for(int j=t;j>=0;j--){
			if(j>=w[i]){
				dp[j]=max(dp[j-w[i]]+val[i],dp[j]);
			}
		}
	}
	cout<

7 P1616 疯狂的采药

#include
#define int long long
using namespace std;
const int N=1e4+5,M=1e7+5; 
int w[N],v[N];
int dp[M]; 
signed main(){
	ios::sync_with_stdio(false);
	int n,W;
	cin>>W>>n;
	for(int i=1;i<=n;i++){
		cin>>w[i]>>v[i];
	}
	for(int i=1;i<=n;i++){
		for(int j=w[i];j<=W;j++){
			dp[j]=max(dp[j],dp[j-w[i]]+v[i]);
		}
	}
	cout<

8 P1802 5 倍经验日（变形01背包）

#include
#define int long long
using namespace std;
const int N=1e3+5; 
int dp[N];
int win[N],lose[N],use[N];
int n,m; 
signed main(){
	ios::sync_with_stdio(false);
	cin>>n>>m;
	for(int i=1;i<=n;i++){
		cin>>lose[i]>>win[i]>>use[i];
	}
	for(int i=1;i<=n;i++){
		for(int j=m;j>=use[i];j--)
			dp[j]=max(dp[j]+lose[i],dp[j-use[i]]+win[i]);
		for(int j=use[i]-1;j>=0;j--)
			dp[j]+=lose[i];
	}
	cout<<5ll*dp[m]<

9 P1002 [NOIP2002 普及组] 过河卒

题解

算法逐渐优化

状态：设 f(i,j)表示从 (1,1) 格子走到当前格子的路径条数

状态转移方程：

//1
#include
#include
#include
#include
#define ll long long
using namespace std;

const int fx[] = {0, -2, -1, 1, 2, 2, 1, -1, -2};
const int fy[] = {0, 1, 2, 2, 1, -1, -2, -2, -1};
//马可以走到的位置

int bx, by, mx, my;
ll f[40][40];
bool s[40][40]; //判断这个点有没有马拦住
int main(){
    scanf("%d%d%d%d", &bx, &by, &mx, &my);
    bx += 2; by += 2; mx += 2; my += 2;
    //坐标+2以防越界
    f[2][1] = 1;//初始化
    s[mx][my] = 1;//标记马的位置
    for(int i = 1; i <= 8; i++) s[mx + fx[i]][my + fy[i]] = 1;
    for(int i = 2; i <= bx; i++){
        for(int j = 2; j <= by; j++){
            if(s[i][j]) continue; // 如果被马拦住就直接跳过
            f[i][j] = f[i - 1][j] + f[i][j - 1];
            //状态转移方程
        }
    }
    printf("%lld\n", f[bx][by]);
    return 0;
} 

//2
#include
#include
#include
#include
#define ll long long
using namespace std;

const int fx[] = {0, -2, -1, 1, 2, 2, 1, -1, -2};
const int fy[] = {0, 1, 2, 2, 1, -1, -2, -2, -1};
int bx, by, mx, my;
ll f[2][40];    //第一维大小为 2 就好
bool s[40][40];

int main(){
    scanf("%d%d%d%d", &bx, &by, &mx, &my);
    bx += 2; by += 2; mx += 2; my += 2;
    f[1][2] = 1; //初始化
    s[mx][my] = 1;
    for(int i = 1; i <= 8; i++) s[mx + fx[i]][my + fy[i]] = 1;
    for(int i = 2; i <= bx; i++){
        for(int j = 2; j <= by; j++){
            if(s[i][j]){
                f[i & 1][j] = 0; //被马拦住了记住清零
                continue;
            }
            f[i & 1][j] = f[(i - 1) & 1][j] + f[i & 1][j - 1]; 
            //新的状态转移方程
        }
    }
    printf("%lld\n", f[bx & 1][by]);
    //输出的时候第一维也要按位与一下
    return 0;
} 

//3
#include
#include
#include
#include
#define ll long long
using namespace std;

// 快速读入
template 
inline void read(I &num){
    num = 0; char c = getchar(), up = c;
    while(!isdigit(c)) up = c, c = getchar();
    while(isdigit(c)) num = (num << 1) + (num << 3) + (c ^ '0'), c = getchar();
    up == '-' ? num = -num : 0; return;
}
template 
inline void read(I &a, I &b) {read(a); read(b);}
template 
inline void read(I &a, I &b, I &c) {read(a); read(b); read(c);}

const int fx[] = {0, -2, -1, 1, 2, 2, 1, -1, -2};
const int fy[] = {0, 1, 2, 2, 1, -1, -2, -2, -1};

int bx, by, mx, my;
ll f[40];   //这次只需要一维数组啦
bool s[40][40];

int main(){
    read(bx, by); read(mx, my);
    bx += 2; by += 2; mx += 2; my += 2;
    f[2] = 1;   //初始化
    s[mx][my] = 1;
    for(int i = 1; i <= 8; i++) s[mx + fx[i]][my + fy[i]] = 1;
    for(int i = 2; i <= bx; i++){
        for(int j = 2; j <= by; j++){
            if(s[i][j]){
                f[j] = 0; // 还是别忘了清零
                continue;
            }
            f[j] += f[j - 1];
            //全新的 简洁的状态转移方程
        }
    }
    printf("%lld\n", f[by]);
    return 0;
} 

//4
#include 
#include 
#include 
#include 
#include 
#include 
#define ll long long

inline int read(){
    int num = 0; char c = getchar();
    while(!isdigit(c)) c = getchar();
    while(isdigit(c)) num = (num << 1) + (num << 3) + (c ^ '0'), c = getchar();
    return num;
}

int bx, by, mx, my;
ll f[30];

inline bool check(int x, int y) {
    if(x == mx && y == my) return 1;
    return (std::abs(mx - x) + std::abs(my - y) == 3) && (std::max ((std::abs(mx - x)), std::abs(my - y)) == 2);
}

int main(){
    bx = read() + 2, by = read() + 2, mx = read() + 2, my = read() + 2;
    f[2] = 1;
    for(int i = 2; i <= bx; i++){
        for(int j = 2; j <= by; j++){
            if(check(i, j)){
                f[j] = 0;
                continue;
            }
            f[j] += f[j - 1];
        }
    }
    printf("%lld\n", f[by]);
    return 0;
} 

---

//【动态规划2】线性状态动态规划

---

10 P1439 【模板】最长公共子序列

题解 LCS转化成LIS+二分法求LIS

对于这个题而言，朴素算法是n^2的，会被10^5卡死，所以我们可以考虑nlogn的做法：因为两个序列都是1~n的全排列，那么两个序列元素互异且相同，也就是说只是位置不同罢了，那么我们通过一个map数组将A序列的数字在B序列中的位置表示出来。

因为最长公共子序列是按位向后比对的，所以a序列每个元素在b序列中的位置如果递增，就说明b中的这个数在a中的这个数整体位置偏后，可以考虑纳入LCS——那么就可以转变成nlogn求用来记录新的位置的map数组中的LIS。

关于为什么可以转化成LIS问题，这里提供一个解释。

A:3 2 1 4 5

B:1 2 3 4 5

我们不妨给它们重新标个号：把3标成a,把2标成b，把1标成c……于是变成：

A: a b c d e
B: c b a d e

这样标号之后，LCS长度显然不会改变。但是出现了一个性质：

两个序列的子序列，一定是A的子序列。而A本身就是单调递增的。
因此这个子序列是单调递增的。

换句话说，只要这个子序列在B中单调递增，它就是A的子序列。

哪个最长呢？当然是B的LIS最长。

自此完成转化。

#include
#define rint register int
using namespace std;
const int maxn=1e5+10;
const int inf =0x7fffffff;
int n,len,a[maxn],b[maxn],mp[maxn],f[maxn]; 
int main(){
	ios::sync_with_stdio(false);
	cin>>n;
	for(int i=1;i<=n;i++){
		cin>>a[i];
		mp[a[i]]=i;//存位置 
	}
	for(int i=1;i<=n;i++){
		cin>>b[i];
		f[i]=inf;
	} 
	len=0; f[0]=0;
	for(int i=1;i<=n;i++){
		int l=0,r=len,mid;
		if(mp[b[i]]>f[len]) f[++len]=mp[b[i]];
		else{
			while(lmp[b[i]]) r=mid;
				else l=mid+1;
			}
			f[l]=min(mp[b[i]],f[l]);
		}
	}
	cout<

//STL
#include
using namespace std;
const int N=101000;
int b[N],idx[N],n;
int read(){
    int x=0,f=1;char ch=getchar();
    while (ch<'0' || ch>'9'){if (ch=='-')f=-1;ch=getchar();}
    while ('0'<=ch && ch<='9'){x=(x<<3)+(x<<1)+(ch^48);ch=getchar();}
    return x*f;
}
int main(){
    n=read();
    memset(b,0x3f,sizeof(b));
    for (int i=1;i<=n;i++)
        idx[read()]=i;
    for (int i=1;i<=n;i++){
        int x=idx[read()];
        *lower_bound(b+1,b+n+1,x)=x;
    }
    printf("%d\n",lower_bound(b+1,b+n+1,b[0])-b-1);
    return 0;
}

11 P1020 [NOIP1999 普及组] 导弹拦截

根据Dilworth定理可知，这题只需要求一个不上升序列长度和一个上升序列长度。

//O(nlogn)DP
#include
#define re register
using namespace std;
const int N=1e5+10;
int a[N],d1[N],d2[N],n;
inline bool read(int &x) {
    char c=getchar();
    if(c==EOF)return false;
    while(c>'9'||c<'0')c=getchar();
    while(c>='0'&&c<='9') {
        x=(x<<1)+(x<<3)+(c^48);
        c=getchar();
    }
    return true;
}
int main(){
	while(read(a[++n]));n--;
	re int len1=1,len2=1;
	d1[1]=d2[1]=a[1];
	for(re int i=2; i<=n; i++) {
        if(d1[len1]>=a[i])d1[++len1]=a[i];
        else *upper_bound(d1+1,d1+1+len1,a[i],greater())=a[i];
        if(d2[len2]

//树状数组
#include
#include
#include
#include
using namespace std;
int f[1000000];
int z[1000000];
int lowbit(int x)
{
    return x&-x;
}
int big;
inline int ask(int x)//这是用来求单调上升子序列的
{
    int r=0;
    for(int i=x;i>0;i-=lowbit(i))
        r=max(r,f[i]);
    return r;
}
inline void add(int x,int v)//这也是用来求单调上升子序列的
{
    for(int i=x;i<=big;i+=lowbit(i))
        f[i]=max(f[i],v);
}
inline int que(int x)//这是用来求最长单调不升子序列的
{
    int r=0;
    for(int i=x;i<=big;i+=lowbit(i))
        r=max(r,f[i]);
    return r;
}
inline void psh(int x,int v)//这也是用来求最长单调不升子序列的
{
    for(int i=x;i>0;i-=lowbit(i))
        f[i]=max(f[i],v);
}
int tot;
int a[1000000];
int ans;
int main()
{
    tot=1;
    while(scanf("%d",&a[tot])!=EOF)
    {
        big=max(big,a[tot]);
        z[tot]=a[tot];
        tot++;
    }
    tot--;//读入并统计个数
    for(int i=1;i<=tot;i++)//求最长单升子序列，树状数组中保存的是0~a[i]的最大值
    {
        int x=ask(a[i])+1;
        ans=max(ans,x);
        add(a[i]+1,x);//因为是严格单升所以这里要+1
    }
    memset(f,0,sizeof(f));//清空树状数组，用来求下面的不降子序列
    int num=0;
    for(int i=1;i<=tot;i++)//求最长不降子序列，树状数组里存的是a[i]~inf的最大值
    {
        int x=que(a[i])+1;
        num=max(num,x);
        psh(a[i],x);//因为是不升而不是严格单降所以不用-1或+1
    }
    printf("%d\n%d\n",num,ans);
    return 0;
}

12 P1280 尼克的任务(线性dp)

①dp

#include
#define int long long 
#define re register
using namespace std;
const int maxn=1e4+10;
int n,k,num=1,sum[maxn],f[maxn];
struct task{//结构体，一起排序，从大到小 
	int start,end;
}t[maxn];
bool cmp(task a,task b){return a.start>b.start;}
signed main(){
	ios::sync_with_stdio(false);
	cin>>n>>k;
	for(re int i=1;i<=k;i++){
		cin>>t[i].start>>t[i].end;
		sum[t[i].start]++;
	}
	sort(t+1,t+k+1,cmp);
	for(re int i=n;i>=1;i--){//倒着搜 
		if(sum[i]==0) f[i]=f[i+1]+1;
		else{
			for(re int j=1;j<=sum[i];j++){
				if(f[i+t[num].end]>f[i]){
					f[i]=f[i+t[num].end];
				}
				num++;//当前已经扫过的任务数 
			}
		} 
	}
	cout<

②最短路

这道题可以用最短路（最长路？）做。

将时间点作为图论的点。

从第P分钟开始，持续时间为T分钟的任务视为从P点到P+T点连一条权为T的边。（边的起点是任务的起始时间，终点是任务结束时间的下一分钟）

如果一个点到最后也没有出度，则向后一个点连边权为0的边（没活干，这一分钟他可以摸鱼。。。）

跑最短路就得到他至少要干多长时间，答案就是（n-最短路结果）

如果将边权作为休息时间的话用最长路也能做

#include
#include
#include
#define N 10005
using namespace std;
struct Edge{
    int to,next,w;
}edge[N*2];
int head[N],tot;
void addedge(int from,int to,int w){
    edge[++tot].to=to;
    edge[tot].w=w;
    edge[tot].next=head[from];
    head[from]=tot;
}
int dis[N];
bool vis[N];
void spfa(){
    memset(dis,0x7f,sizeof(dis));
    dis[1]=0;
    queue q;
    q.push(1);
    int now;
    while(!q.empty()){
        now=q.front();
        q.pop();
        vis[now]=false;
        for(int i=head[now];i;i=edge[i].next){
            if(dis[edge[i].to]>dis[now]+edge[i].w){
                dis[edge[i].to]=dis[now]+edge[i].w;
                if(!vis[edge[i].to]){
                    q.push(edge[i].to);
                    vis[edge[i].to]=true;
                }
            }
        }
    }
}
int main(){
    int n,k,p,t;
    scanf("%d%d",&n,&k);
    while(k--){
        scanf("%d%d",&p,&t);
        addedge(p,p+t,t);
    }
    for(int i=1;i<=n;++i){
        if(head[i]==0){
            addedge(i,i+1,0);
        }
    }
    spfa();
    printf("%d\n",n-dis[n+1]);
}

13 P2758 编辑距离

假设用f[i][j]表示将串a[1…i]转换为串b[1…j]所需的最少操作次数（最短距离）

首先是边界：

①i==0时，即a为空，那么对应的f[0][j]的值就为j：增加j个字符，使a转化为b

②j==0时，即b为空，那么对应的f[i][0]的值就为i：减少i个字符，使a转化为b

然后考虑一般情况（这里是DP思想）：我们要得到将a[1..i]经过最少次数的操作就转化为b[1..j]，那么我们就必须在此之前以最少次数（假设为k次）的操作,使现在的a和b只需再做一次操作或者不做操作就可以使a[1..i]转化到b[1..j]。而“之前”有三种情况：

①将a[1…i]转化为b[1…j-1]

②将a[1..i-1]转化为b[1..j]

③将a[1…i-1]转化为b[1…j-1]

第①种情况，只需要在最后将a[j]加上b[1..i]就可以了，总共就需要k+1次操作。

第②种情况，只需要在最后将a[i]删除，总共需要k+1个操作。

第③种情况，只需要在最后将a[i]替换为b[j]，总共需要k+1个操作。但如果a[i]刚好等于b[j]，就不用再替换了，那就只需要k个操作。

为了得到最小值，将以上三种情况的最小值作为f[i][j]的值（我前面不是说了f[i][j]表示串a[1…i]转换为串b[1…j]所需的最少操作次数嘛）,最后答案在f[n][m]中。

状态转移方程：

 

实现（只描述算法部分）

初始化。边界情况，用循环嵌套或两个独立的循环都可以做到。

2.循环嵌套遍历f数组，先处理a[i]==b[j]的情况，如不满足，再从三种情况中选择最小的，作为f[i][j]的值。三种情况中，①如果在k个操作里将a[1…i-1]转换为b[1..j]，那就可以将a[i]删除，共需k+1个操作，所以是f[i-1][j]+1;②如果在k个操作里将a[1…i]转换为b[1…j-1] ，那就可以加上b[j]，共需k+1个操作；③如果我们可以在k个操作里将a[1…i-1]转换为b[1…j-1]，那就可以将a[i]转换为b[j]，也是共需k+1个操作。（前面已经处理过了a[i]==b[j]的情况）

3.最后的答案是f[][]最后一个元素的值。

#include
#define re register
using namespace std;
const int maxn=2e3+10;
int f[maxn][maxn],lena,lenb;
char a[maxn],b[maxn];
void dp(){
	for(re int i=1;i<=lena;i++) f[i][0]=i;
	for(re int j=1;j<=lenb;j++) f[0][j]=j;
	for(re int i=1;i<=lena;i++){
		for(re int j=1;j<=lenb;j++){
			if(a[i-1]==b[j-1]) f[i][j]=f[i-1][j-1];
			else f[i][j]=min(min(f[i-1][j],f[i][j-1]),f[i-1][j-1])+1;
		}
	}
}
int main(){
	scanf("%s %s",a,b);
	lena=strlen(a);
	lenb=strlen(b);
	dp();
	printf("%d\n",f[lena][lenb]);
	return 0;
}

14 P1040 [NOIP2003 提高组] 加分二叉树（区间dp*）

首先，我们要做的就是设计状态，其实就是设计dp数组的含义，它要满足无后效性。
关注这个 左子树*右子树+根 我只要知道左子树分数和右子树分数和根的分数（已给出），不就可以了吗？管他子树长什么样！
所以，我们ff数组存的就是最大分数，怎么存呢？
我们发现：子树是一个或多个节点的集合。
那么我们可不可以开一个f[i][j]来表示节点i到节点j成树的最大加分呢？可以先保留这个想法（毕竟暂时也想不到更好的了）。

如果这样话，我们就来设计状态转移方程。
按照刚刚的设计来说的话，我们的答案就是f[1][n]了，那么我们可以从小的子树开始，也就是len，区间长度。有了区间长度我们就要枚举区间起点，i为区间起点，然后就可以算出区间终点j。
通过加分二叉树的式子我们可以知道，二叉树的分取决于谁是根，于是我们就在区间内枚举根k。
特别的，f[i][i]=a[i]f[i][i]=a[i]其中a[i]为第i个节点的分数。
因为是要求最大值，所以我们就可以设计出

于是乎，我们就自己设计出了一个dp过程，因为是顺着来的，所以很少有不成立的。

至于输出前序遍历，我们再设计一个状态root[i][j]来表示节点i到节点j成树的最大加分所选的根节点。
所以我们按照根->左->右的顺序递归输出即可。

①区间dp

#include
#define int long long
#define re register
using namespace std;
const int maxn=50;
int n;
int f[maxn][maxn],root[maxn][maxn];
void print(int l,int r){//前序遍历 
	if(l>r) return;
	cout<>n;
	for(re int i=1;i<=n;i++){
		cin>>f[i][i];
		f[i][i-1]=1;
		root[i][i]=i;
	}
	for(re int len=1;len

②记忆化搜索

#include
#include
using namespace std;
int n,v[49],dp[49][49],root[49][49];
int ser(int l,int r){
    if(dp[l][r]>0)return dp[l][r];
    if(l==r)return v[l];
    if(rdp[l][r]){
            dp[l][r]=p;root[l][r]=i;
        }
    }
    return dp[l][r];
}
void print(int l,int r){
    if(r

15 P4933 大师

对于两个数字，他们组成的等差数列的公差一定是一样的

那么我们不必去枚举公差，直接枚举第 i 个数前面那个数，得到公差进行转移即可

用 f[i][j]表示以 i 结尾公差为 j 的等差数列个数。

以 i结尾且上一个数是 j 的公差为 k 的等差数列数量是以 j 结尾公差为 k 的等差数列数加一

转移的过程中直接计数，顺便把数字数为一的区间加上

注意第二维数组开二倍将负数右移即可

这样只需要 n^2 的转移就可以了

#include
#define re register
using namespace std;
const int p=20000;
const int mod=998244353;
int f[1005][40005];
int a[1005];
int n,ans;
int main(){
	cin>>n;
	for(re int i=1;i<=n;i++) cin>>a[i];
	for(re int i=1;i<=n;i++){
		ans++;
		for(re int j=i-1;j>0;j--){
			f[i][a[i]-a[j]+p]+=f[j][a[i]-a[j]+p]+1;
			f[i][a[i]-a[j]+p]%=mod;
			ans+=f[j][a[i]-a[j]+p]+1;
			ans%=mod;
		}
	}
	cout<

16 P1077 [NOIP2012 普及组] 摆花

题解 更多题解看这个

①【解题思路】

这一题乍一看有些难度，理解后看一下觉得其实还蛮简单的。

主要思路是：先开一个二维数组b[][]，存储放i种j盆花的方案总数。

首先进行初始化，大家想想,无论有多少种花，如果一盆都没有，那是不是只有一种方案总数了（什么也不放）？

所以初始化为b[i][0]=1(0<=i<=m)。然后呢，我们进行三重循环。变量i表示有多少种花，j表示有多少盆花，k则是用于计算某种花放多少盆。

从总盆数开始循环到总盆数-最大盆数，如果k小于0（说明最大盆数大于总盆数）就退出循环。我们得到的状态转移方程则是：

b[i][j]+=b[i-1][k](j>=k>=j-a[i])

最终的答案就是b[n][m]

当然，随时加上%1000007会更保险。然后就AC啦。

//dp
#include
#define re register
using namespace std;
const int mod=1e6+7;
int n,m;
int a[105],f[105][105];
int main(){
	cin>>n>>m;
	for(re int i=1;i<=n;i++) cin>>a[i];
	for(re int i=0;i<=m;i++) f[i][0]=1;//初始化，不管有多少种花，只要是0盆花，就只有1种可能性，啥都不放
	for(re int i=1;i<=n;i++){//几种花
		for(re int j=1;j<=m;j++){//几盆花
			for(re int k=j;k>=j-a[i];k--){//这种花放多少盆？我们用变量k来循环
				if(k>=0){
					f[i][j]+=f[i-1][k]%mod;
					f[i][j]%=mod;
				}else break; //如果超出限制就退出循环
			}
		}
	}
	cout<

//dalao dp
#include
using namespace std;
const int maxn=105, mod = 1000007;
int n, m, a[maxn], f[maxn][maxn];
int main()
{
    cin>>n>>m;
    for(int i=1; i<=n; i++) cin>>a[i];
    f[0][0] = 1;
    for(int i=1; i<=n; i++)
       for(int j=0; j<=m; j++)
           for(int k=0; k<=min(j, a[i]); k++)
              f[i][j] = (f[i][j] + f[i-1][j-k])%mod;
    cout<

②所谓记忆化，其实就是用一个数组将搜索过的值存起来，避免重复搜索，从而提高效率。（有必要可以上网搜一下，会搜索的应该很容易理解记忆化吧）

时间复杂度大概是：O(nma_i)O(nmai​) 吧，100%的数据稳过

//记忆化搜索
#include
using namespace std;
const int maxn=105, mod = 1000007;
int n, m, a[maxn], rmb[maxn][maxn];
int dfs(int x,int k)
{
    if(k > m) return 0;
    if(k == m) return 1;
    if(x == n+1) return 0;
    if(rmb[x][k]) return rmb[x][k]; //搜过了就返回
    int ans = 0;
    for(int i=0; i<=a[x]; i++) ans = (ans + dfs(x+1, k+i))%mod;
    rmb[x][k] = ans; //记录当前状态的结果
    return ans;
}
int main()
{
    cin>>n>>m;
    for(int i=1; i<=n; i++) cin>>a[i];
    cout<

17 P1233 木棍加工

DP求最大上升子序列

先根据长度从高到低排序，如果长度相同，再根据宽度从高到低排序。

如果是在同一次准备周期里面，前面的木棍一定在后面木棍之前被加工。

这样，这个问题就转化成了在n个数中，求不下降子序列最少个数。

根据dilworth定理，不下降子序列最小个数等于最大上升子序列的长度。

于是乎，问题又简化成求n个数的最大上升子序列

//O(n^2)
#include
using namespace std;
struct MG{
	int l,w;
	bool operator < (const MG& x)const{//重定向小于号用于排序
		return l==x.l?w>x.w:l>x.l;
	}
}m[5050];
int f[5050];//dp
int n,ans;
int main(){
	cin>>n;
	for(int i=0;i>m[i].l>>m[i].w;
	sort(m,m+n);//根据先前重定向的小于号排序
	//for(int i=0;i=0;j--){
			if(m[i].w>m[j].w) f[i]=max(f[i],f[j]+1);
		}
		ans=max(ans,f[i]);//更新ans的值 
	}
	cout<

O(nlogn)的方法：f[i] 表示长度为 i 的(木棒宽度的)上升子序列结尾最小是多少，在 f[ans] 比当前木棒宽度小时更新 ans，否则二分查找( f数组显然单调)找到比当前木棒宽度大的第一个位置更新。

这里就可以说明为什么要 l 相同时按 w 降序，我们需要答案尽量小，而以 w 降序时可以不浪费时间的按顺序加工完，因此这样排序，对应到模型里就是减少最长上升子序列的长度 

//O(nlogn)
#include
using namespace std;
//快读
const int lenc=1e5;
inline char gc(){
	static char buf[lenc],*p1,*p2;
	return p1==p2&&(p2=(p1=buf)+fread(buf,1,lenc,stdin),p1==p2)?EOF:*p1++;
}
inline int read(){
	register int q=0;
	register char c=gc();
	while(!isdigit(c))
		c=gc();
	while(isdigit(c))
		q=(q<<3)+(q<<1)+(c^48),c=gc();
	return q;
} 
//快读结束
struct stick{
	int l,w;
}a[5010]; 
bool cmp(stick q,stick w){
	if(q.l!=w.l) return q.l>w.l;
	return q.w>w.w;
}
int n,ans,f[5010];
int main(){
	n=read();
	for(register int i=1;i<=n;i++)
		a[i].l=read(),a[i].w=read();
	sort(a+1,a+1+n,cmp);
	for(register int i=1;i<=n;i++){
		if(a[i].w>f[ans]) f[++ans]=a[i].w;
		else{
			int tmp=lower_bound(f+1,f+1+ans,a[i].w)-f;
			f[tmp]=a[i].w;
		}
	}
	printf("%d\n",ans);
	return 0;
}

贪心。

先将长度排序，再依次寻找宽度不上升序列，将它们全部标记，最后寻找没有被标记的。

//贪心
#include
using namespace std;
struct thing{
	int lo,wi;
}t[5005];//木棍定义为结构体
bool comp(thing& a,thing& b){
	if(a.lo==b.lo) return a.wi>b.wi;
	return a.lo>b.lo;
}//定义比较函数，先按从高到低排列长度，长度相同的按从高到低排列宽度
bool used[5005]={};//是否被处理过
int n,sum,twi;
int main(){
	ios::sync_with_stdio(false);//取消输入流同步，加快输入速度
	cin>>n;
	for(int i=1;i<=n;i++) cin>>t[i].lo>>t[i].wi;//输入
	sort(t+1,t+n+1,comp);//排序
	for(int i=1;i<=n;i++){
		if(used[i]==0){//如果这个木棍被处理过就跳过
			twi=t[i].wi;//保存现有宽度
			for(int j=i+1;j<=n;j++){//向后搜索
				if(t[j].wi<=twi&&used[j]==0){//如果有宽度小于现有宽度且没有被处理过
					used[j]=1;//处理这个木棍
					twi=t[j].wi;//保存这个木棍的宽度 
				} 
			} 
		}
	}
	for(int i=1;i<=n;i++){
		if(used[i]==0) sum++;//如果没用过就加1分钟
	} 
	cout<

18 P1091 [NOIP2004 提高组] 合唱队形

本人觉得这题是很不错的，虽然难度不高。首先，我们要想出列最少，那么就想要留下的最多。很容易想的最长升，但是，这个序列是一个中间高，两头底的序列，最长升只能处理出单调性的序列。

那么怎么做到呢？

我们先看从T1到Ti这一段单调递增的序列，再看Ti到TK这一段单调递减的序列，那么问题就解决了。先从1到n求一趟最长升，然后从n到1也求一趟，最后枚举中间的Ti，然后从众多Ti中挑个大的。

#include
using namespace std;
//快读
const int lenc=1e5;
inline char gc(){
	static char buf[lenc],*p1,*p2;
	return p1==p2&&(p2=(p1=buf)+fread(buf,1,lenc,stdin),p1==p2)?EOF:*p1++;
}
inline int read(){
	register int q=0;
	register char c=gc();
	while(!isdigit(c))
		c=gc();
	while(isdigit(c))
		q=(q<<3)+(q<<1)+(c^48),c=gc();
	return q;
} 
//快读结束
int n,ans,a[105],f[2][105];
int main(){
	n=read();
	for(int i=1;i<=n;i++) a[i]=read();
	a[0]=0;
	//从1到n求最长升 
	for(int i=1;i<=n;i++){
		for(int j=0;ja[j]){
				f[0][i]=max(f[0][i],f[0][j]+1);
			}
		} 
	}
	a[n+1]=0;
	//从n到1求最长升 
	for(int i=n;i>=1;i--){
		for(int j=n+1;j>i;j--){
			if(a[i]>a[j]){
				f[1][i]=max(f[1][i],f[1][j]+1);
			}
		} 
	} 
	for(int i=1;i<=n;i++) ans=max(f[0][i]+f[1][i]-1,ans);//枚举Ti，从1到Ti的最长升+从TK到Ti的最长升-1(Ti被加了两次)
	printf("%d\n",n-ans);
	return 0;
}

//动态规划+线段树+离散化
#include
#define N 200001
#define INF INT_MAX
using namespace std;
struct node{
	int left,right,v;
};
struct point{
	int v,id;
};
int n,ans=INF;
int a[N],c[N],f1[N],f2[N];
point b[N];
node tree[N*4];
bool cmp(point x,point y){
	return x.v>1;
	BuildTree(i<<1,L,m);
	BuildTree(i<<1|1,m+1,R);
	PushUp(i);
	return;
}
void Change(int i,int index,int s){
	if (tree[i].left==tree[i].right){
		tree[i].v=max(tree[i].v,s);
		return;
	}
	if (index<=tree[i<<1].right) Change(i<<1,index,s); else Change(i<<1|1,index,s);
	PushUp(i);
	return;
}
int Query(int i,int L,int R){
	if (L<=tree[i].left&&R>=tree[i].right) return tree[i].v;
	int t=0;
	if (L<=tree[i<<1].right) t=max(t,Query(i<<1,L,R));
	if (R>=tree[i<<1|1].left) t=max(t,Query(i<<1|1,L,R));
	return t;
}
void work(int *w){
	BuildTree(1,1,n);
	for (int i=1;i<=n;i++){
		if (a[i]==1) w[i]=1; else w[i]=Query(1,1,a[i]-1)+1;
		Change(1,a[i],w[i]);
	}
	return;
}
int main(){
	scanf("%d",&n);
	for (int i=1;i<=n;i++) {
		scanf("%d",&b[i].v);
		b[i].id=i;
		c[i]=i;
	}
	sort(b+1,b+n+1,cmp);
	for (int i=2;i<=n;i++) if (b[i].v==b[i-1].v) c[i]=c[i-1];
	for (int i=1;i<=n;i++) a[b[i].id]=c[i];
	work(f1);
	for (int i=1;i<=n/2;i++) swap(a[i],a[n-i+1]);
	work(f2);
	for (int i=1;i<=n/2;i++) swap(f2[i],f2[n-i+1]);
	for (int i=1;i<=n;i++) ans=min(ans,n-f1[i]-f2[i]+1);
	printf("%d\n",ans);
	return 0;
}

19 P5858 「SWTR-03」Golden Sword

考虑到要顺序放置，贡献与当前锅内的原料有关，所以我们考虑将这两个东西加入我们的 dp 式。

设 dp{i,j}​为放进 i 原料，且当时正有 j 个原料所得到的最大耐久度。有 dp 方程：

//单调队列优化dp（推荐下面一个）
#include
using namespace std;
long long n,m,s,a[5505],dp[5505][5505],q[5505],pos[5505];
int main(){
	scanf("%lld %lld %lld",&n,&m,&s);
	for(long long i=1;i<=n;++i)	scanf("%lld",&a[i]);
	for(long long i=0;i<=n;++i)	for(long long j=0;j<=m;++j)	dp[i][j]=-1008600110086001;
	dp[0][0]=0;
	for(long long i=1;i<=n;++i)
	{
		int l=1,r=1;
		q[l]=dp[i-1][m];
		pos[l]=m;
		for(long long j=m;j;--j)
		{
			while(pos[l]>j+s-1 && l<=r)	++l;
			while(q[r]

//单调队列优化dp
#include
#define ll long long
using namespace std;
inline int read(){//快读
	int x=0,sign=1;char s=getchar();
	while(!isdigit(s)){
		if(s=='-')sign=-1;
		s=getchar();
	}
	while(isdigit(s)){
		x=(x<<1)+(x<<3)+(s^48);
		s=getchar();
	}
	return x*sign;
}
const int N=5555;
const ll inf=1ll<<60;
int n,w,s;
ll ans=-inf,a[N],dp[N][N];
struct monotone_queue{//单调队列
	int head,tail,id[N];
	ll d[N];
	inline void init(){
		head=1,tail=0;
	}
	inline void push(ll v,int x){//第一个参数为dp[i][x]
		while(head<=tail&&d[tail]<=v)tail--;
		d[++tail]=v;
		id[tail]=x;
	}
	inline void pop(int x){//弹出
		while(head<=tail&&id[head]-x>=s)head++;
	}
}q;
int main()
{
	n=read(),w=read(),s=read();
	for(int i=1;i<=n;i++)a[i]=read();
	dp[1][1]=a[1];
	for(int i=2;i<=n;i++){
		q.init();
		if(i>w)q.push(dp[i-1][w],w);//注意特判细节
		for(int j=min(w,i);j>=1;j--){
			if(j>1)q.push(dp[i-1][j-1],j-1);//先插入
			q.pop(j);//再弹出
			dp[i][j]=q.d[q.head]+1ll*a[i]*j;//O(1)转移 
		}
	}
	for(int j=1;j<=w;j++)ans=max(ans,dp[n][j]);//求答案
	cout<

20 P1880 [NOI1995] 石子合并

石子合并的GarsiaWachs算法

题解

#include
using namespace std;
const int inf=0x7fffffff;
int n,temp,te,maxn,minn=inf;
int cnt[210],s[210][210],f1[210][210],f2[210][210];
int main(){
	cin>>n;
	for(int i=1;i<=n;i++){
		cin>>cnt[i];
		cnt[i]+=cnt[i-1];
		s[i][i]=i;
		s[i+n][i+n]=i+n;
	}
	for(int i=1;i<=n;i++) cnt[i+n]=cnt[i]+cnt[n];
	for(int i=n*2;i>=1;i--){
		for(int j=i+1;j<=n*2;j++){
			temp=inf;
			f2[i][j]=max(f2[i+1][j],f2[i][j-1])+cnt[j]-cnt[i-1];
			for(int k=s[i][j-1];k<=s[i+1][j];k++){
				if(temp>f1[i][k]+f1[k+1][j]+cnt[j]-cnt[i-1]){
					temp=f1[i][k]+f1[k+1][j]+cnt[j]-cnt[i-1];
					te=k;
				}
			}
			f1[i][j]=temp;
			s[i][j]=te;
		}
	}
	for(int i=1;i<=n;i++){
		minn=min(minn,f1[i][i+n-1]);
		maxn=max(maxn,f2[i][i+n-1]);
	}
	printf("%d\n%d\n",minn,maxn);
	return 0;
}

#include  
#include  
#include  
using namespace std;   
int n,minl,maxl,f1[300][300],f2[300][300],num[300];  
int s[300];  
inline int d(int i,int j){return s[j]-s[i-1];}  
//转移方程：f[i][j] = max(f[i][k]+f[k+1][j]+d[i][j];
int main()  
{   
    scanf("%d",&n);  
    for(int i=1;i<=n;i++)  //好吧，终于有时间看看评论区，看来大家对这里异议蛮多的，这里统一解释一下，因为是一个环，所以需要开到两倍再枚举分界线，最后肯定是最大的 
    {  
        scanf("%d",&num[i]);    
    }  
    for(int i=1;i<=n+n;i++){
    	num[i+n]=num[i];  
        s[i]=s[i-1]+num[i];
	}
    for(int p=1;p

21 P1220 关路灯

22 P3205 [HNOI2010]合唱队

我们发现区间dp有一个性质——大区间包涵小区间，这道题就符合这样的一个性质

如何设计状态

那么我们要怎么设计状态，我们想，每个人进入队伍里，只有2种可能，1种是从左边加入，另外1种是从右边进入，所以我们的状态是有3个数

f[i][j][0]表示的是第i人从左边进来的方案数

f[i][j][1]表示的是第j人从右边进来的方案数

推导状态转移方程

从左边进来肯定前1个人比他高，前1个人有2种情况，要么在i+1号位置，要么在j号位置。

同理，从右边进来肯定前1个人比他矮，前1个人有2种情况，要么在j-1号位置，要么在i号位置。

那么状态转移方程就出来了。

if(a[i]a[i])f[i][j][1]+=f[i][j-1][0];
if(a[j]>a[j-1])f[i][j][1]+=f[i][j-1][1];
f[i][j][0]%=19650827;
f[i][j][1]%=19650827;

边界条件 

当i=j的时候显然只有一种方案，所以边界条件是

for(int i=1;i<=n;i++)f[i][i][0]=1,f[i][i][1]=1;

然而你会发现你WA了，为什么

因为，只有一个人的时候方案只有一种，可是我们这里却有2种方案，所以我们得默认1个人的时候，是从左边进来，于是我们就有了正确的边界条件

for(int i=1;i<=n;i++)f[i][i][0]=1;

#include
using namespace std;
const int mod=19650827;
int f[2010][2010][2],a[2010];
int main(){
	int n;
	cin>>n;
	for(int i=1;i<=n;i++) cin>>a[i];
	for(int i=1;i<=n;i++) f[i][i][0]=1;//边界条件
	for(int len=1;len<=n;len++){
		for(int i=1,j=i+len;j<=n;i++,j++){
			if(a[i]a[i]) f[i][j][1]+=f[i][j-1][0];
			if(a[j]>a[j-1]) f[i][j][1]+=f[i][j-1][1];
			f[i][j][0]%=mod;
			f[i][j][1]%=mod; 
		}
	} 
	cout<<(f[1][n][0]+f[1][n][1])%mod<

23 P1063 [NOIP2006 提高组] 能量项链

简单的说：给你一项链，项链上有n颗珠子。相邻的两颗珠子可以合并(两个合并成一个)。合并的同时会放出一定的能量。不同的珠子的合并所释放的能量是不同的。问：按照怎样的次序合并才能使释放的能量最多？

//区间动规 
//重点就是将整体划分为区间，小区间之间合并获得大区间
//状态转移方程的推导如下
//一、将珠子划分为两个珠子一个区间时，这个区间的能量=左边珠子*右边珠子*右边珠子的下一个珠子
//二、区间包含3个珠子，可以是左边单个珠子的区间+右边两珠子的区间，或者左边两珠子的区间右边+单个珠子的区间 
//即，先合并两个珠子的区间，释放能量，加上单个珠子区间的能量（单个珠子没有能量。。）
//Energy=max(两个珠子的区间的能量+单个珠子区间的能量，单个珠子的区间的能量+两个珠子的区间的能量 ） 
//三、继续推4个珠子的区间，5个珠子的区间。
//于是可以得到方程：Energy=max（不操作的能量，左区间合并后的能量+右区间合并后的能量+两区间合并产生能量）
//两区间合并后产生的能量=左区间第一个珠子*右区间第一个珠子*总区间后面的一个珠子

#include
using namespace std;
int n,e[300],f[300][300],maxn=-1;
int main(){
	cin>>n;
	for(int i=1;i<=n;i++){
		cin>>e[i];
		e[i+n]=e[i];
	}//珠子由环拆分为链，重复存储一遍
	for(int i=2;i<2*n;i++){
		for(int j=i-1;i-j=1;j--){//从i开始向前推
			for(int k=j;kmaxn) maxn=f[j][i];//更新最大值 
		}
	} 
	cout<

24 P1005 [NOIP2007 提高组] 矩阵取数游戏

25 P3146 [USACO16OPEN]248 G

题解

#include
using namespace std;
const int maxn=255;
const int INF=0x3f3f3f3f;
int n,val,ans;
int f[maxn][maxn];
int main(){
	cin>>n;
	for(int i=1;i<=n;i++){
		cin>>val;
		f[i][i]=val;// 预处理，当不进行合并时得到的价值就是自己 
	}
	for(int len=2;len<=n;len++){// 枚举所合并区间的长度，因为转移是从小区间转移到大区间，所以要从小到大枚举区间的长度
		for(int i=1;i<=n-len+1;i++){// 枚举区间的左端点 ，当左端点等于  全长 减去 区间长度 再加一  的时候，右端点取到序列的最右边 
			int j=i+len-1;
			for(int pos=i;pos

26 P4170 [CQOI2007]涂色

#include
using namespace std;
const int maxn=255;
const int INF=0x3f3f3f3f;
char s[52];
int f[52][52];
int main(){
	int n;
	cin>>s+1;
	n=strlen(s+1);
	memset(f,0x7f,sizeof(f));//由于求最小，于是应初始化为大数
	for(int i=1;i<=n;i++){
		f[i][i]=1;
	}
	for(int len=1;len

27 CF607B Zuma