深入浅出雷达脉冲压缩技术
本文讲脉冲压缩技术。我在学习的时候也查过很多资料,尤其是网上搜到的资料,基本都不太清楚或者不好理解。我想通过自己的努力把脉冲压缩技术的今生前世讲讲清楚。
本文是我的第一篇文章,我是一名技术爱好者,典型的理科生,但是文科实在不行,最终高考和考研都没能上名校,倒不是说我理工科不行,而是文科太拖后腿。
一、基础准备
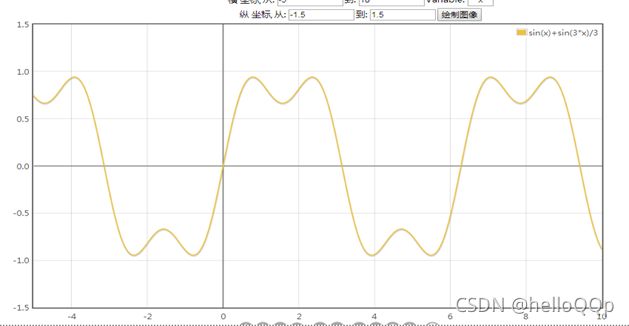
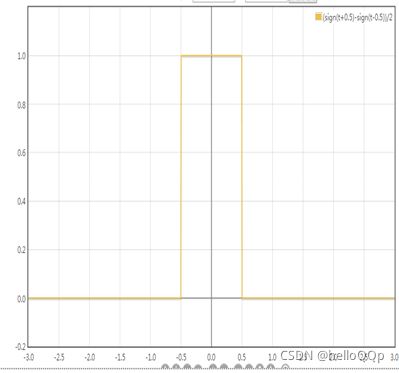
信号与系统(或者高数中的傅里叶级数,复变函数中的傅里叶变换)告诉我们一个随时间变化的信号,可以看做是不同频率信号的叠加。如下面三幅图片,是不同频率信号不断叠加,最后近似为一个方波,在工程中,本来就有干扰和噪声,叠加到一定程度就可以忽略误差而认为他就是了。
那么对于一个雷达发射的脉冲信号而言,其频率成分是怎么样的呢?通过傅里叶变换计算得到了下图,类似一个阻尼震荡,工程上一般认为这个信号的频谱宽度为1/τ(τ为时域信号的脉冲宽度),当然这是有误差的,但前面说了,这点误差实际中是可以忽略的。
二、脉冲压缩的提出
(一)雷达分辨力
脉冲雷达的大致工作过程是:发射一个短脉冲(大喊一声)、同时按下计时器,然后接收回波(听回声)、并把收到回波的时刻记录下来、算出距离,最后再转动角度继续上面的操作。这样的工作方式存在一个问题,如下图,如果两个物体比较近,小于脉冲宽度的一半时,这两个物体的回波就会重叠在一起,在雷达的回波图形上就会显示成一个回波,无法区分是否为两个物体。这就是雷达分辨力这一技术指标。请注意是分辨力,是分辨两个物体的能力,不是分辨率。应该说分辨力越小越好。
(二)雷达作用距离
雷达作用距离可用雷达方程来理论计算,雷达方程有多种形式,大多是通过变量代换变出来的。网上找了个用信号能量表示的雷达方程,如下图最后。意思是说,最大最用距离与发射信号的能量E(功率*发射持续时间)有关。可见雷达想看得远,就需要提高E,除了提高功率外,只能增加发射脉冲宽度。这里提一个题外的小问题:对于一部雷达,假设远处F的回波已经小于噪声,雷达已经无法探测F。此时我单纯地增加发射信号的宽度,是否能探测到F?正如我小喊一声,无法听到回声。此时我不增加喊声强度,只增加喊声的持续时间,是否可以听到回声?如果能回答,那么对雷达方程的认识已经不在表面。请读者自己思考,如果完全理解本文思想,应该能回答出来,欢迎留言讨论。
(三)鱼和熊掌兼得——脉冲压缩
通过前文介绍,如果想要提高距离分辨力,就需要减小发射脉冲的宽度;如果想要提高最大作用距离,就需要增大发射脉冲的宽度。于是距离分辨力和最大作用距离之间产生矛盾,两者不可兼得。
究其本质原因,是发射脉冲的时宽(宽度)与发射带宽成反比,即τ=C/B,其中τ为时宽;C为常数,通常取1;B为发射带宽,也是接收机的带宽,会影响接收机的灵敏度,进而影响最大作用距离。由此可见,在常规脉冲雷达中时宽带宽积(B╳τ)是个常数,而时宽影响距离分辨力,带宽影响最大作用距离,这是产生矛盾的内在逻辑。
那么是否可以通过一种技术来提高时宽带宽积,从而解决这一矛盾呢?单纯地通过减小脉宽(常规脉冲雷达)肯定不行,必须使用其他调制方式。如在脉冲持续时间不变的前提下,在脉冲持续期间采用调频波方式来增加带宽,从而提高时宽带宽积。同时在接收回波信号时,采用匹配滤波器将信号“压缩”成窄脉冲,于是解决了距离分辨力和最大作用距离之间的矛盾。同时通过“压缩”,还提高了信噪比。
三、脉冲压缩怎么做
发射时:
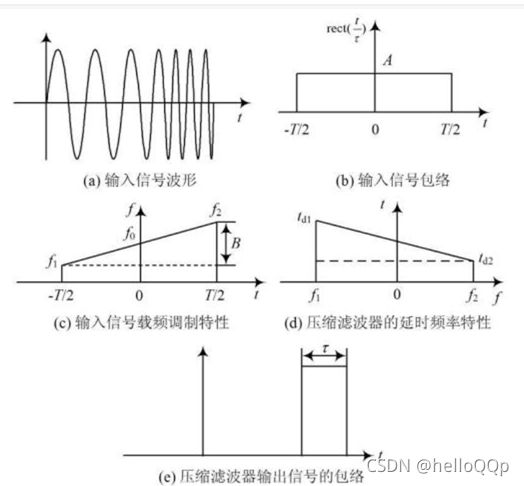
必须使用其他调制方式。如在脉冲持续时间不变的前提下,在脉冲持续期间采用调频波方式来增加带宽(F2-F1),从而提高时宽带宽积。下图是发射信号脉冲持续期间的时域波形和频谱。所以很多资料上说的chip、啁啾,其实就是这个调频波。当然线性调频只是一直方式,也可以采用非线性调频、或者采用数字方式加入扰码也是一样的,都是在在脉冲持续时间不变的前提下增加了带宽。
接收时:
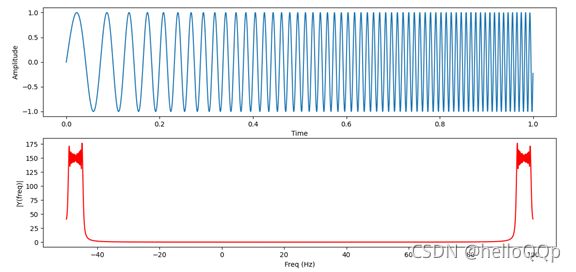
对于这样的回波,采用匹配滤波器将信号“压缩”成窄脉冲,于是解决了距离分辨力和最大作用距离之间的矛盾。同时通过“压缩”,还提高了信噪比。下图蓝色为时域波形,红色为频谱。压缩后,输出的脉冲会变得很窄、且幅度很大,从图上看由1变到600以上(直观的理解是面积不变)。对于接收机来说,最终处理的是压缩后的窄脉冲,分辨力由该窄脉冲决定,与发射的长脉冲无关。本质上来讲,是经过了匹配滤波器,也有一些资料中说是做卷积,那是因为现在都采用了数字信号处理,匹配滤波器采用数学电路实现(应该是FIR滤波器那种)。在数字处理电路中,经过滤波器也可以用卷积来实现(即信号与系统中常说的,频域上的乘积就是时域上的卷积).
也在网上找了个示意图,大概的压缩过程如下图
四、脉冲压缩的本质
到此为止,对于数学很棒,通信原理很懂的人来说,应该是看懂了。但是可能大多数人会觉得很奇怪,输入的信号是这样的,输出信号怎么就变成一个窄脉冲了呢?那我们继续吧。
怎么理解脉冲压缩?将问题简化而不失一般性。
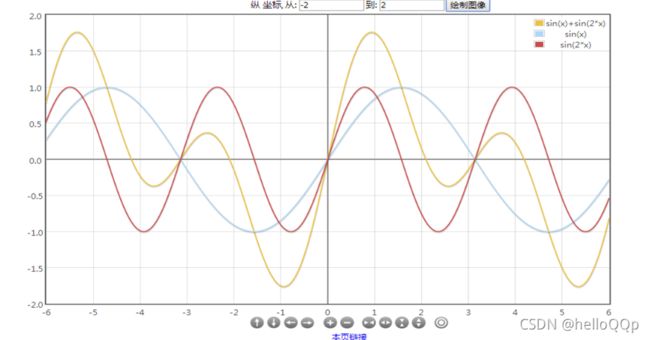
假设我要传输一个信号,我采用的发射波形是下图黄色这样的,这个信号有两个频率分量。那么我在接收的时候,我应该如何利用信号,使性能最佳?当然我也可以直接按照最常规的方法去接收,但是这不是最佳的,比如当底噪比较大,为1.9时,你就无法接收该信号的。
那么怎么办呢?就是要最大化地利用信号,发射信号是我自己发射的,对我来说他的频谱和各分量的相位是已知的,我只要做下图处理即可。就是把这个已知的发射信号的所有频谱分量的波峰对对齐,使输出信号在某一个时刻上有个共振(这一时刻,所有的频谱信号都是波峰),这就是最大限度地利用了已知发射信号,也不可能存在另一个比他还要大的情况。而噪声的相位是随机的,经过这样的相位移动后,底噪的幅度还是于原来一样。这么一叠加脉冲自然是变窄了一些。叠加的结果为2,即使噪声大于原接收波形,通过技术处理后也能提取回波。而这个技术处理这就是通过匹配滤波器。具体的严密计算论证亲参阅通信原理书中描述(配滤波器严格的做法是:1)对某一时刻的相位偏差进行修正,都修正到一个值上,使所有频率都同相相加,如上述内容。2)对幅度大的频率分量响应大,对幅度小的频率分量响应小,可以直观理解为频率分量大的地方信噪比占优,需要放大的多一些,上述内容两个频率分量大小一样,所以没有讨论)。那么有人要问了,为什么要搞得这么复杂呢,直接发射这样的共振信号不就完了?工程所限,如果直接发共振信号,那么发射机的电压就会很高。如果不采用共振信号,在接收时对齐共振,可以减小发射机功率,或在发射功率一定的情况下有更好的作用距离。笔者见过压缩后,信号能增强100倍的情况。如果直接让发射机电压增大100,那太恐怖了。
再从简单到复杂,前面的数学基础中讲到信号可以看成是不同频率的叠加。一个线性调频波是F1到F2的频率信号的叠加。接收时,经过匹配滤波器,把这些频率信号的波峰都对其,就产生了脉冲压缩的效果(脉宽变小很多,幅度变大很多)。
五、脉冲压缩理解举例
在光线通信中,
1)在发射端产生一束强窄白光。
2)由于紫光传播速度慢于红光,进过很长距离的传播,变成了一束弱宽色彩分离的光。类似线性调频波。
3)在接收端,进行修正,其过程与传播过程相反——让紫光追上红光。类似脉冲压缩处理。
4)于是又产生了一束窄白光。
六、脉冲压缩的优缺点
七、总结提高
脉冲压缩一词是从直观的效果来讲的,看起来像是让面积保持不变,把长脉冲挤压成短脉冲而增加了脉冲的幅度。比如100微秒的脉冲压缩成1微秒后,那么幅度增加100倍。但是这样的叫法太过肤浅,有时还有误导成分。我一开始看到这一词语时,咋一看以为是:检测脉冲的幅度和持续时间;然后保持面积不变,脉冲宽度减小n倍,同时脉冲幅度增加n倍。这显然是不对的,因为想要脉冲增加多少倍,只是软件上乘上一个数,想多大就多大;时间上想短一点只要截取一段就可以,想多短就多短。关键是当信号淹没在噪声中时你怎么去找脉冲?所以这样的处理毫无意义。
仔细一看,原来是匹配滤波器。所以从工程的角度来讲它主要依靠匹配滤波器来实现目标。
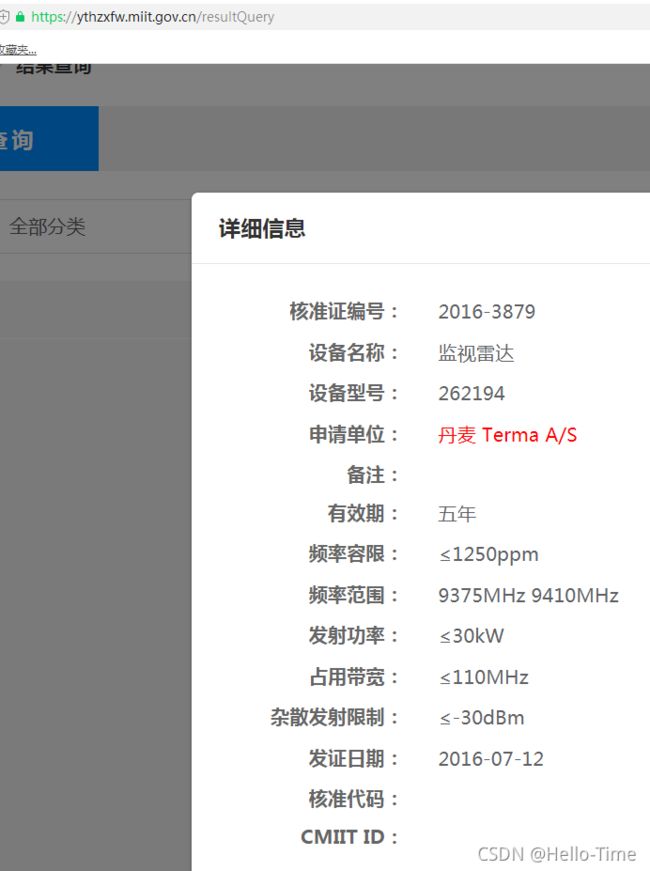
那么为什么可以这样呢,可以在不损失分辨力的前提下增加作用距离呢?本质上是增加了信号的带宽。从通信理论来看,根据从香农公式,这是一种扩频通信。在码元速率(类似雷达每秒发射的脉冲数量)不变的前提下,通过增加带宽来提高信噪比,从而增加了作用距离。对于雷达来说也是有损失的,这个损失就是带宽,需要占用更大的带宽,才能来解决这一对矛盾。那么有接触过雷达的人又要问了。如下图,从工信部网站上找来的两个海事雷达的核准证,两者应用场景一样,应该说作用距离相当。一个发射功率为50w,一个为30Kw,可见前者采用了脉压技术。那么为何占用的带宽还是后者比前者大很多呢?请读者自己思考,如果完全理解本文思想,应该能回答出来,欢迎留言讨论。
另外,脉冲压缩后时域上的波形中,次高峰与最高峰的比值是衡量脉压的一个技术指标。如果次高峰也很高,那么在雷达原始图像上会:强回波的径向前后存在次高峰产生的回波图像,这是由脉压引起的雷达假目标。
纯粹的线性调频波不是最优的,需要加各种窗(如海明窗等),或采用其他复杂一点的调频方式(如非线性调频)来提高这一指标。
至此,将其来龙去脉讲解完毕!