数据结构—— 基于二叉树的算术表达式求值

实验五 基于二叉树的算术表达式求值

数据结构——中序表达式求值（栈实现）
实验目的：
1.掌握二叉树的二叉链表存储表示和二叉树的遍历等基本算法。
2.掌握根据中缀表达式创建表达式树的算法
3.掌握基于表达式树的表达式求值算法。
实验内容：
问题描述
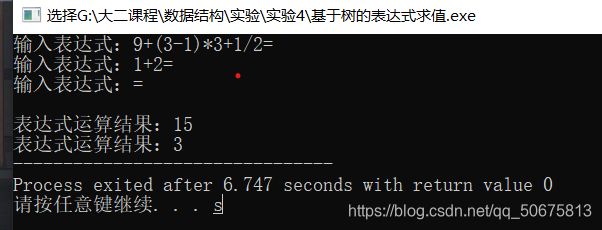
输入一个表达式(表达式中的数均为小于10的正整数),利用二叉树来表示该表达式,创建表达式树,然后利用二叉树的遍历操作求表达式的值。
输入要求：
多组数据,每组数据一行,对应一个算术表达式,每个表达式均以“=”结尾。当表达式只有一个“=”时,输入结束。
输出要求
每组数据输出1行,为表达式的值。

输出样例
15
3
【实验提示】
首先,读入表达式,参照算法6.4创建一个基于二叉链表表示的表达式树;然后,对表达式树进行后序遍历,得到表达式的值。
【扩展提示】
对于任意一个算术表达式,都可用二叉树来表示。表达式对应的二叉树创建后,利用二叉树的遍历等操作,很容易实现表达式的求值运算。因此问题的关键就是如何创建表达式树,下面讨论由中缀表达式创建表达式树的方法。
假设运算符均为双目运算符,则表达式对应的表达式树中叶子结点均为操作数,分支结点均为运算符。由于创建的表达式树需要准确的表达运算次序,因此在扫描表达式创建表达式树的过程中,当遇到运算符时不能直接创建结点,而应将其与前面的运算符进行优先级比较,根据比较的结果再进行处理。这种处理方式类似于第4章的表达式求值算法中的运算符的比较,可以借助一个运算符栈,来暂存已经扫描到的还未处理的运算符。
根据表达式树与表达式对应关系的递归定义,每两个操作数和一个运算符就可以建立一棵表达式二叉树,而该二叉树又可以作为另一个运算符结点的一棵子树。可以另外借助一个表达式树栈,来暂存已建立好的表达式树的根结点,以便其作为另一个运算符结点的子树而被引用。

为实现表达式树的创建算法

可以使用两个工作栈,一个称做OPTR,用以暂存运算符;另一个称做EXPT,用以暂存已建立好的表达式树的根结点。
为了便于实现,假设每个表达式均以”#”开始,以”#”结束。
表达式树的创建算法步骤
① 初始化OPTR栈和EXPT栈,将表达式起始符“#”压入OPTR栈。
②扫描表达式,读入第一个字符ch,如果表达式没有扫描完毕至“#”或OPTR的栈顶元素不为“#”时,则循环执行以下操作：
i）若ch不是运算符,则以ch为根创建一棵只有根结点的二叉树,且将该树根结点压入EXPT栈,读入下一字符ch；
ii）若ch是运算符,则根据OPTR的栈顶元素和ch的优先级比较结果,做不同的处理:
若是小于,则ch压入OPTR栈,读入下一字符ch；
若是大于,则弹出OPTR栈顶的运算符,从EXPT栈弹出两个表达式子树的根
结点,以该运算符为根结点,以EXPT找中弹出的第二个子树作为左子树,以
EXPT中弹出的第一个子树作为右子树,创建一棵新二叉树,并将该树根结点压入EXPT栈；
若是等于，则OPTR的栈顶元素是“（”且ch是“）”，这时弹出OPTR 栈顶的“（”,相当于括号匹配成功，然后读入下一字符ch。

void EvaluateExpression(BiTree &root,char *str)
{
	SqStack OPTR;
	InitStack(&OPTR);
	SqStack_BiTree EXPT;	
	SqStack_BiTree_InitStack(EXPT);
	
	char ch,x,theta;
	BiTree a,b;
	int i=0;
	
	Push(&OPTR, '=');   //=是表达式结束符
		ch =str[i++];
	GetTop(&OPTR, &x);
	while(ch != '=' || x != '=')
	{
		if(In(ch))   //是7种运算符之一
		{
			switch(Precede(x, ch))
			{
			case '<':   //当前已经压栈一个运算符（x）比后一个运算符（c）低时，就将c压栈
				Push(&OPTR, ch);
				ch =str[i++];
				break;
			
			case '='://消除小括号 
				Pop(&OPTR, &x); //脱括号并接收下一字符 
				ch =str[i++];			
				break;
			case '>':
				Pop(&OPTR,&theta);
				BiTree TEMP;
				TEMP=(BiNode*)malloc(sizeof(BiNode));
				if(!TEMP)
					exit(-1);
				TEMP->data=theta;	
				SqStack_BiTree_Pop(EXPT,b);
				SqStack_BiTree_Pop(EXPT,a);
				
				TEMP->lchild=a;
				TEMP->rchild=b;
				SqStack_BiTree_Push(EXPT,TEMP);
			
				
				root=TEMP;
				break;
			}
		}

		if(ch>='0'&&ch<='9')
			{
				BiTree Temp;
				Temp=(BiNode*)malloc(sizeof(BiNode));
				if(!Temp)
					exit(-1);
				Temp->data=ch;
				Temp->lchild=NULL;
				Temp->rchild=NULL;
				SqStack_BiTree_Push(EXPT,Temp);
			
				ch=ch =str[i++];;	
			}
		
		
		
		GetTop(&OPTR, &x);
		
 	}

}

标题表达式树的求值算法步骤

① 设变量lvalue和 rvalue分别用以记录表达式树中左子树和右子树的值,初始均为0。
② 如果当前结点为叶子(结点为操作数),则返回该结点的数值，否则(结点为运算符)执行以下操作：
递归计算左子树的值记为 lvalue
递归计算右子树的值记为 rvalue
根据当前结点运算符的类型，将lvalue和rvalue进行相应运算并返回。

int	calculate_BiTree(BiTree &T)
{
	int lvalue;
	int rvalue;
	char theta;
	if(T==NULL)	return 0;
	if(T!=NULL)
	{
		if(T->lchild==NULL&&T->lchild==NULL)
			return T->data-'0';
		else
		{
			lvalue=calculate_BiTree(T->lchild);
			rvalue=calculate_BiTree(T->rchild);
			theta=T->data;
			
			return Operate(lvalue,theta,rvalue);
		}	
	}	
}

全部代码（可直接运行）

#include
#include 
#define TRUE 1
#define FALSE 0
#define OK 1
#define ERROR 0

#define STACK_INIT_SIZE 100   //存储空间初始分配量
#define STACKINCREMENT 10   //存储空间分配增量
typedef int Status; 
typedef char TElemType;//表达式求值的运算类型
typedef int ElemType;
typedef struct BiNode
{
	TElemType data;
	struct BiNode *lchild;
	struct BiNode *rchild;
}BiNode,*BiTree;
typedef BiTree SBElemType;

int  preorderTraverse(BiTree T)//二叉树的先序递归遍历算法 
{
	if(T==NULL)
		return 0;
	else 
		{
			printf("%c ",T->data);
			preorderTraverse(T->lchild);
			preorderTraverse(T->rchild);
		}
 } 

int InorderTraverse(BiTree T)//二叉树的中序递归遍历算法 
{
	if(T==NULL)
		return 0;
	else 
		{
			InorderTraverse(T->lchild);
			printf("%c",T->data);
			InorderTraverse(T->rchild);
		}
 }


int  PostorderTraverse(BiTree T)//二叉树的后序递归遍历算法 
{
	if(T==NULL)
		return 0;
	else 
		{
			PostorderTraverse(T->lchild);
			PostorderTraverse(T->rchild);
			printf("%c ",T->data);
		}
 }
 
 
 
typedef struct
{
	TElemType *base;
	TElemType *top;
	int stacksize;
}SqStack;


//构造一个空栈
Status InitStack(SqStack *S)
{
	S->base = (TElemType *)malloc(STACK_INIT_SIZE * sizeof(TElemType));
	if(!S->base)
	{
		printf("内存分配失败!\n");
		exit(0);
	}

	S->top = S->base;
	S->stacksize = STACK_INIT_SIZE;
	return OK;
}

//若栈不为空，则用e返回S的栈顶元素，并返回OK；否则返回ERROR
Status GetTop(SqStack *S, TElemType *e)
{
	if(S->top == S->base)
		return ERROR;

	*e = *(S->top - 1);
	return OK;
}

//插入元素e为新的栈顶元素
Status Push(SqStack *S, TElemType e)
{
	if(S->top - S->base >= STACK_INIT_SIZE)   //栈满， 追加存储空间
	{
		S->base = (TElemType *)realloc(S->base, (S->stacksize + STACKINCREMENT) * sizeof(TElemType));
		if(!S->base)
		{
			printf("内存分配失败!\n");
			exit(OVERFLOW);
		}

		S->top = S->base + S->stacksize;
		S->stacksize += STACKINCREMENT;
	}

	*S->top++ = e;
	
	return OK;
}

//若栈不为空，则删除S的栈顶元素，用e返回其值，并返回Ok；否则返回ERROR
Status Pop(SqStack *S, TElemType *e)
{
	if(S->top == S->base)
		return ERROR;

	*e =  *--S->top;

	return OK;
}






typedef struct {
  SBElemType *base; 	// 栈底指针
  SBElemType *top; 	// 栈顶指针
  int stacksize; 	// 栈空间大小
} SqStack_BiTree;


void SqStack_BiTree_InitStack(SqStack_BiTree &S)
{
    // 构造一个空栈S
    if(!(S.base = (SBElemType *)malloc(STACK_INIT_SIZE 
                                  * sizeof(SBElemType))))
        exit(0);     // 存储分配失败
    S.top = S.base;
    S.stacksize = STACK_INIT_SIZE;
}

void SqStack_BiTree_DestroyStack(SqStack_BiTree &S)
{
    // 销毁栈S，S不再存在
    free(S.base);
    S.base = NULL;
    S.top = NULL;
    S.stacksize = 0;
}

void SqStack_BiTree_Push(SqStack_BiTree &S, SBElemType e)
{
    if(S.top - S.base >= S.stacksize) { // 栈满，追加存储空间
        S.base = (SBElemType *)realloc(S.base, (S.stacksize 
              + STACKINCREMENT) * sizeof(SBElemType));
        if(!S.base)
            exit(OVERFLOW);           // 存储分配失败
        S.top = S.base + S.stacksize;
        S.stacksize += STACKINCREMENT;
    }
    *(S.top)++ = e;
}

Status SqStack_BiTree_Pop(SqStack_BiTree &S, SBElemType &e)
{
    // 若栈不空，则删除S的栈顶元素，用e返回其值，并返回OK；
    // 否则返回ERROR
    if(S.top == S.base)
        {
        	//printf("此时栈为空，不可以再出栈\n");
			return ERROR;
		}
    e = *--S.top;
    //printf("当前出栈的元素的值为：%d\n",e);
    
    return OK;
}

Status SqStack_BiTree_GetTop(SqStack_BiTree S, SBElemType &e)
{
    // 若栈不空，则用e返回S的栈顶元素，并返回OK；
    // 否则返回ERROR
    if(S.top > S.base) {
        e = *(S.top - 1);
        //printf("输出栈顶元素为 %d \n",e);
        return OK;
    }
    else
    {
    	//printf("此时栈为空，得不到栈顶元素\n");
		return ERROR;
	}
        
}




//根据教科书表3.1，判断两符号的优先关系
char Precede(char t1, char t2)
{  
	int i,j;  
    char pre[7][7]={           
    //运算符之间的优先级制作成一张表格  
        {'>','>','<','<','<','>','>'},  
        {'>','>','<','<','<','>','>'},  
        {'>','>','>','>','<','>','>'},  
        {'>','>','>','>','<','>','>'},  
        {'<','<','<','<','<','=','0'},  
        {'>','>','>','>','0','>','>'},  
        {'<','<','<','<','<','0','='}};  
    switch(t1){  
        case '+': i=0; break;  
        case '-': i=1; break;  
        case '*': i=2; break;  
        case '/': i=3; break;  
        case '(': i=4; break;  
        case ')': i=5; break;  
        case '=': i=6; break;  
    }  
    switch(t2){  
        case '+': j=0; break;  
        case '-': j=1; break;  
        case '*': j=2; break;  
        case '/': j=3; break;  
        case '(': j=4; break;  
        case ')': j=5; break;  
        case '=': j=6; break;  
    }  
    return pre[i][j];  
}  
//判断c是否为运算符
Status In(TElemType c)
{
	switch(c)
	{
	case '+':
	case '-':
	case '*':
	case '/':
	case '(':
	case ')':
	case '=':
		return TRUE;
	default:
		return FALSE;
	}

}

//二元运算(a theta b)
ElemType Operate(ElemType a, TElemType theta, ElemType b)
{
	TElemType c;
	switch(theta)
	{
	case '+':
		c = a + b;
		break;
	case '-':
		c = a - b;
		break;
	case '*':
		c = a * b;
		break;
	case '/':
		c = a / b;
		break;
	}
	return c;
}



void EvaluateExpression(BiTree &root,char *str)
{
	SqStack OPTR;
	InitStack(&OPTR);
	SqStack_BiTree EXPT;	
	SqStack_BiTree_InitStack(EXPT);
	
	char ch,x,theta;
	BiTree a,b;
	int i=0;
	
	Push(&OPTR, '=');   //=是表达式结束符
		ch =str[i++];
	GetTop(&OPTR, &x);
	while(ch != '=' || x != '=')
	{
		if(In(ch))   //是7种运算符之一
		{
			switch(Precede(x, ch))
			{
			case '<':   //当前已经压栈一个运算符（x）比后一个运算符（c）低时，就将c压栈
				Push(&OPTR, ch);
				ch =str[i++];
				break;
			
			case '='://消除小括号 
				Pop(&OPTR, &x); //脱括号并接收下一字符 
				ch =str[i++];			
				break;
			case '>':
				Pop(&OPTR,&theta);
				BiTree TEMP;
				TEMP=(BiNode*)malloc(sizeof(BiNode));
				if(!TEMP)
					exit(-1);
				TEMP->data=theta;	
				SqStack_BiTree_Pop(EXPT,b);
				SqStack_BiTree_Pop(EXPT,a);
				
				TEMP->lchild=a;
				TEMP->rchild=b;
				SqStack_BiTree_Push(EXPT,TEMP);
			
				
				root=TEMP;
				break;
			}
		}

		if(ch>='0'&&ch<='9')
			{
				BiTree Temp;
				Temp=(BiNode*)malloc(sizeof(BiNode));
				if(!Temp)
					exit(-1);
				Temp->data=ch;
				Temp->lchild=NULL;
				Temp->rchild=NULL;
				SqStack_BiTree_Push(EXPT,Temp);
			
				ch=ch =str[i++];;	
			}
		
		
		
		GetTop(&OPTR, &x);
		
 	}

}

int	calculate_BiTree(BiTree &T)
{
	int lvalue;
	int rvalue;
	char theta;
	if(T==NULL)	return 0;
	if(T!=NULL)
	{
		if(T->lchild==NULL&&T->lchild==NULL)
			return T->data-'0';
		else
		{
			lvalue=calculate_BiTree(T->lchild);
			rvalue=calculate_BiTree(T->rchild);
			theta=T->data;
			
			return Operate(lvalue,theta,rvalue);
		}	
	}	
}


int main()
{
	BiTree T;
	char str[1000];
	int result[100]={0};
	int number=0;
	do
	{
		printf("输入表达式：");
		gets(str);
		EvaluateExpression(T,str);
		result[number]=calculate_BiTree(T);
		number++;
	}while(strcmp(str,"=")!=0);
	

	for(int j=0;j<number-1;j++)
	{
		printf("\n表达式运算结果：%d",result[j]);
	}


	
}