C++ AB组辅导课
C++ AB组辅导课
- 蓝桥杯C++ AB组辅导课 第一讲 递归与递推 Acwing
-
- 1、整数划分(递归)
- 2、acwing92. 递归实现指数型枚举
- 10凑算式(全排列)
- 11李白打酒(全排列)
- 12、棋牌总数(递归)
- 13、剪邮票(递归)
- 14、1050. 鸣人的影分身 (递归或动态规划(记忆化搜索))
- 15、方格分割 (dfs+思维)
- 蓝桥杯C++ AB组辅导课 第三讲 数学与简单DP
-
- 4、包子凑数
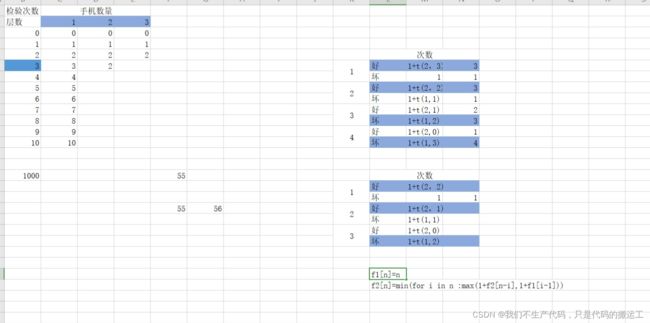
- 5、测试次数(最优解问题——>dp)
- 数论
- 3、acwing2058. 笨拙的手指(进制转换)
- 4、AcWing 1346. 回文平方(回文判断、进制转换)
- 6、AcWing 428. 数列(二进制,映射)
- 7、1431分糖果
- 蓝桥杯C++ AB组辅导课 第四讲 枚举、模拟与排序 Acwing
-
- 1、AcWing 1210.连号区间数(枚举)
- 5、AcWing466.回文日期(回文,日期,模拟)
- 7、AcWing1229.日期问题(字符串+时间格式)
- 图论
- 1、acwing2019. 拖拉机(最短路径+双向队列)
- 往年题目汇总
-
- 2015-2018
- 2013年
- 2018年
- 2019年
- 2020年
- 2021年
- (8)、其他进制转化为十进制
-
- 十进制转化成其他进制:短除法
- 其他进制转化成十进制:秦九韶算法
蓝桥杯C++ AB组辅导课 第一讲 递归与递推 Acwing
1、整数划分(递归)
算法设计与分析——分治与递归——整数划分问题
#include2、acwing92. 递归实现指数型枚举
#include 10凑算式(全排列)
凑算式
B DEF
A + --- + ------- = 10
C GHI
(如果显示有问题,可以参见【图1.jpg】)
这个算式中A~I代表1~9的数字,不同的字母代表不同的数字。
比如:
6+8/3+952/714 就是一种解法,
5+3/1+972/486 是另一种解法。
这个算式一共有多少种解法?
注意:你提交应该是个整数,不要填写任何多余的内容或说明性文字。
#include11李白打酒(全排列)
话说大诗人李白,一生好饮。幸好他从不开车。
一天,他提着酒壶,从家里出来,酒壶中有酒2斗。他边走边唱:
无事街上走,提壶去打酒。
逢店加一倍,遇花喝一斗。
这一路上,他一共遇到店5次,遇到花10次,已知最后一次遇到的是花,他正好把酒喝光了。
请你计算李白遇到店和花的次序,可以把遇店记为a,遇花记为b。则:babaabbabbabbbb 就是合理的次序。像这样的答案一共有多少呢?请你计算出所有可能方案的个数(包含题目给出的)。
注意:通过浏览器提交答案。答案是个整数。不要书写任何多余的内容。
#include 12、棋牌总数(递归)
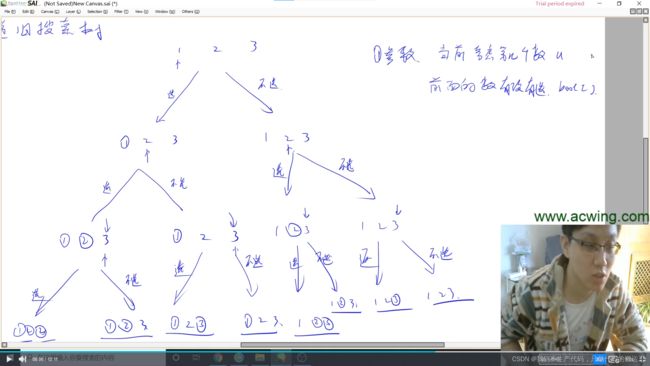
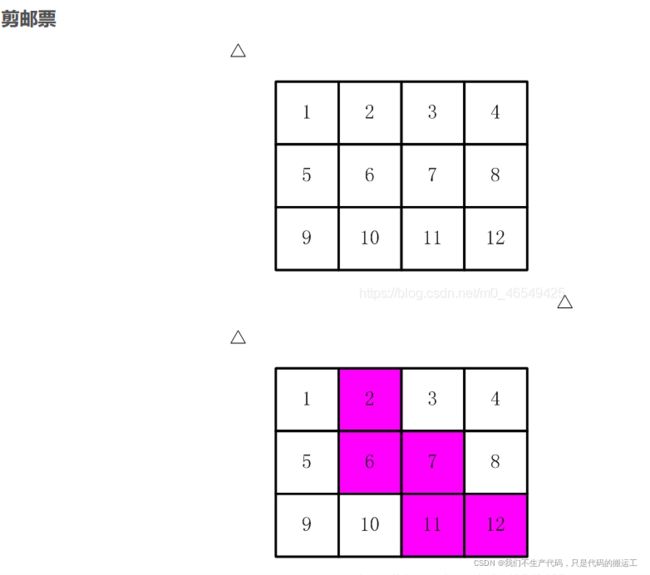
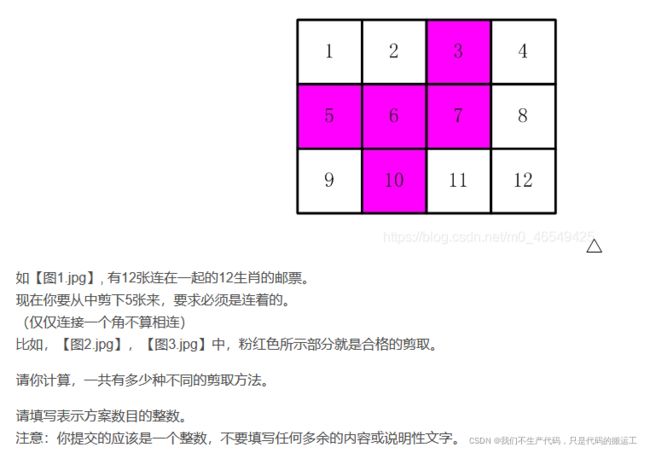
#include13、剪邮票(递归)
详解
#include14、1050. 鸣人的影分身 (递归或动态规划(记忆化搜索))
这道题目相当于是把n个苹果放m个盘子里的一道题.
题目:
把M个同样的苹果放在N个同样的盘子里,允许有的盘子空着不放,问共有多少种不同的分法?(用K表示)5,1,1和1,5,1 是同一种分法。
解题分析:
设f(m,n)为m个苹果,n个盘子的放法数目,则先对n作讨论,
当n>m:则必定有n-m个盘子永远空着,去掉它们对摆放苹果方法数目不产生影响。即 if(n>m) f(m,n) = f(m,m)
当n <= m:不同的放法可以分成两类:含有0的方案数,不含有0的方案数
1、含有0的方案数,即有至少一个盘子空着,即相当于 f(m,n)=f(m,n-1);
2、不含有0的方案数,即所有的盘子都有苹果,相当于可以从每个盘子中拿掉一个苹果,不影响不同放法的数目,即 f(m,n)=f(m-n,n).而总的放苹果的放法数目等于两者的和,即 f(m,n)=f(m,n-1)+f(m-n,n)
递归出口条件说明:
当n=1时,所有苹果都必须放在一个盘子里,所以返回1;
当m==0(没有苹果可放)时,定义为1种放法;
#include实际上我们可以发现,在递归的过程中就是要用到之前的数据,继而这道题可以转换为记忆化搜索将结果保存来做,即dp做法,但是这个dp是从递归去思考出来的- -而不是像灿总那样直接思考dp做法.
#include15、方格分割 (dfs+思维)
题目描述:
6x6的方格,沿着格子的边线剪开成两部分。要求这两部分的形状完全相同。
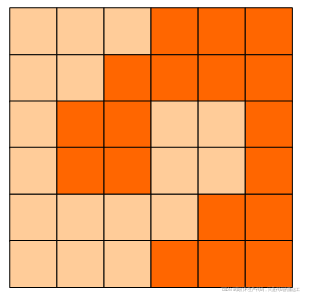
试计算:包括这3种分法在内,一共有多少种不同的分割方法。注意:旋转对称的属于同一种分割法。
请提交该整数,不要填写任何多余的内容或说明文字。
如果把样例图案剪开,发现有且只有两个点在边界上,且一定经过 (3,3)点。以(3,3)为起点进行深搜,深搜到一个边界上的点,那么他的中心对称点相当于也搜过了。如果发现搜到了边界,那么它的中心对称点也到了边界 沿着已经搜过的点剪开,那么剪开的两个图形为中心对称图形。(要注意最终的结果要除以4)
例如 我们从(3,3)点出发一直向右到边界 , 或一直向左,或一直向上,或一直向下剪出来的图形是同一个。
#include蓝桥杯C++ AB组辅导课 第三讲 数学与简单DP
4、包子凑数
包子凑数
(1)在什么情况下,包子凑不出来的数目是无限个;
(2)如何知道包子能凑出哪些数目;
第一个问题
关键其实就是知道假如输入的每笼包子的数目不互质的话,包子凑不出来的数目就是无限个;
一直反复来求两个数的公约数,假如最后不是1,那么就说这两个数不互质,求出两个数的最大公约数之后在和后面的数又进行比较,
gcd函数返回两个或多个整数的最大公约数
第二个问题
包子凑数里面说了笼数是无穷笼,所以可以利用完全背包里面的转移方程来解决:
#include5、测试次数(最优解问题——>dp)
题解
#include数论
3、acwing2058. 笨拙的手指(进制转换)
acwing2058. 笨拙的手指(进制转换)
4、AcWing 1346. 回文平方(回文判断、进制转换)
AcWing 1346. 回文平方
视频讲解
附带的知识点和题解
6、AcWing 428. 数列(二进制,映射)
AcWing 428. 数列
#include7、1431分糖果
#include 蓝桥杯C++ AB组辅导课 第四讲 枚举、模拟与排序 Acwing
1、AcWing 1210.连号区间数(枚举)
连号区间数
区间中最大值与最小值差等于区间长度
//给定的序列是包含1到N的所有数
#include5、AcWing466.回文日期(回文,日期,模拟)
AcWing466.回文日期
/*
(枚举,模拟) O(104)
由于只有八位数,而且回文串左右对称,因此可以只枚举左半边,这样只需枚举 0~9999
总共一万个数,然后判断:
整个八位数构成的日期是否合法;
是否在范围内
*/
#include7、AcWing1229.日期问题(字符串+时间格式)
AcWing1229.日期问题
set输出默认按字典序输出
/*
日期问题
https://www.acwing.com/problem/content/description/1231/
*/
#include
//仅有三种格式 年月日 --- 日月年 --- 月日年
getans(a,b,c);
getans(c,a,b);
getans(c,b,a);
for(auto x:ans)
cout<<x<<endl;
}
图论
1、acwing2019. 拖拉机(最短路径+双向队列)
acwing2019. 拖拉机(最短路径)
往年题目汇总
2015-2018
2015-2018
2012-2019
2013年
2013
2018年
2018
2019年
2019
2020年
2020
2021年
2021
(8)、其他进制转化为十进制
十进制转化成其他进制:短除法
// 将数字转换为字符
char get(int x)
{
if(x <= 9) return x + '0';
else return x - 10 + 'A';
}
// 进制转换,十进制转换为b进制
string base(int n,int b)
{
string num;
while(n){
num += get(n % b), n /= b;//num中保留余数
}
reverse(num.begin(),num.end());//逆置一下num
return num;
}
其他进制转化成十进制:秦九韶算法
// 将字符转换为数字
int uget(char c)
{
if(c <= '9') return c - '0';
return c - 'A' + 10;
}
// 将b进制转换为十进制,秦九韶算法
int base10(string num, int b)
{
int res = 0;
for(auto c : num)//从高位到低位 ,枚举一位
res = res * b + uget(c);
return res;
}
int get(string s,int b)//将其他进制转化为十进制算法
{
int res=0;
//秦九韶算法
for(auto c:s)
res = res * b + c - '0';//平时所用的进制转换 需要将c(字符)转化为数字
return res;
}
问题:acwing:笨拙的手指