数据结构---归并排序和外部排序
内部排序
若整个排序过程不需要访问外存便能完成,则称此类排序问题为内部排序。
外部排序
若参加排序的记录数量很大,整个序列的排序过程不可能在内存中完成,则称此类排序问题为外部排序。
就地排序
若排序算法所需的辅助空间并不依赖于问题的规模n,即辅助空间为O(1),称为就地排序。
稳定排序
假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序后,这些记录的相对次序保持不变,即在原序列中 ri=rj, ri 在 rj 之前,而在排序后的序列中,ri 仍在 rj 之前,则称这种排序算法是稳定的;否则称为不稳定的。
排序序列分布
排序需要考虑待排序关键字的分布情况,这会影响对排序算法的选择,通常我们在分析下列算法时都考虑关键字分布是随机分布的,不是按照某种规律分布的,比如正态分布等。
待排序序列
排序序列中,剩余即将要排序的序列部分。
已排序序列
排序序列中,已经排序好的序列部分
首先我们了解一下归并排序的特性:
- 归并的缺点在于需要O(N)的空间复杂度,归并排序的思考更多的是解决在磁盘中的外排序问题。
- 时间复杂度:O(N*logN)
- 空间复杂度:O(N)
- 稳定性:稳定
归并排序(MERGE-SORT)是建立在归并操作上的一种有效的排序算法,该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有 序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。 归并排序核心步骤
- 将我们的排序的数组进行我们的重点划分为两个部分
例如left和right此时的区间是[left,right),制定一个中点mid = (left+right)/2。 - 利用分治算法继续将我们左右两个继续进行划分,
- 知道我们的left == right 或者left+1 == right,也就是只有一个元素的时候和一个元素也没有的时候我们就认为这个序列是有序的
- 然后将我们的有序的数组进行合并,达到我们最后的时候就合成了有序的数组。
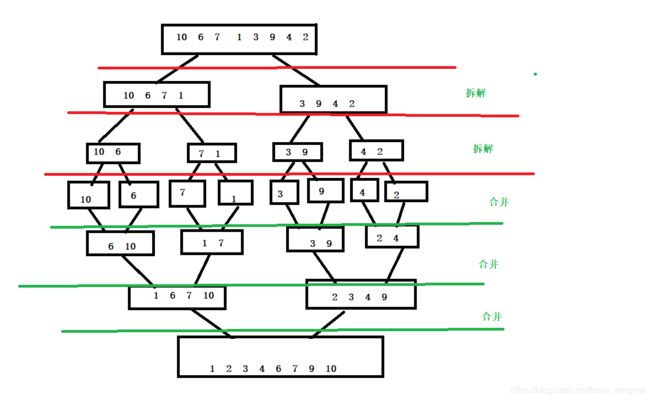
就上图一样,我们将数组每次拆解成两个部分,知道达到有序数组的条件的时候就开始合并我们的数组。这就是我们二路归并
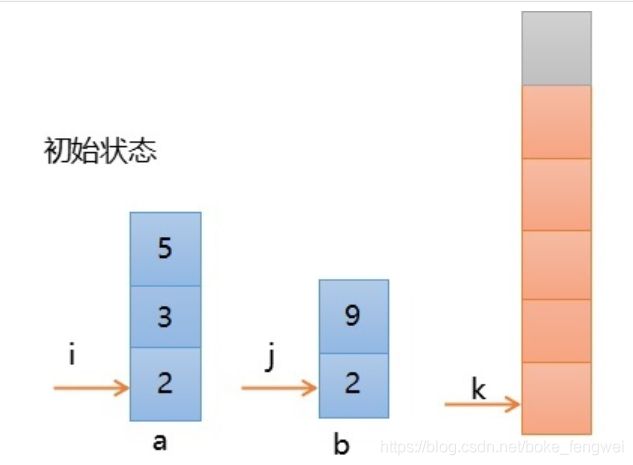
如下图所示,初始状态时,a序列[2,3,5]和b序列[2,9]为已排序好的子序列,现在利用二路归并,将a和b合并为有序序列 r,初始时,i指向a的第一个元素,j指向b的第一个元素,k初始值等于0。
说明,r中最后一个元素起到哨兵的作用,灰色显示。
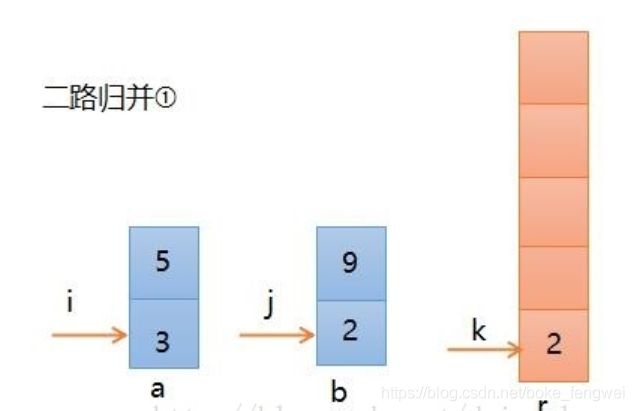
第一步,比较a[i]和b[j],发现相等,如果规定相等时,a的先进入r,则如下图所示,i, k分别加1,为了形象化,归并后的元素不再绘制。
第二步,继续比较,此时b[j]小,所以b的元素2进入r,则如下图所示,j, k分别加1,

第三步,继续比较,此时a[i]小,所以a的元素3进入r,则如下图所示,i, k分别加1,
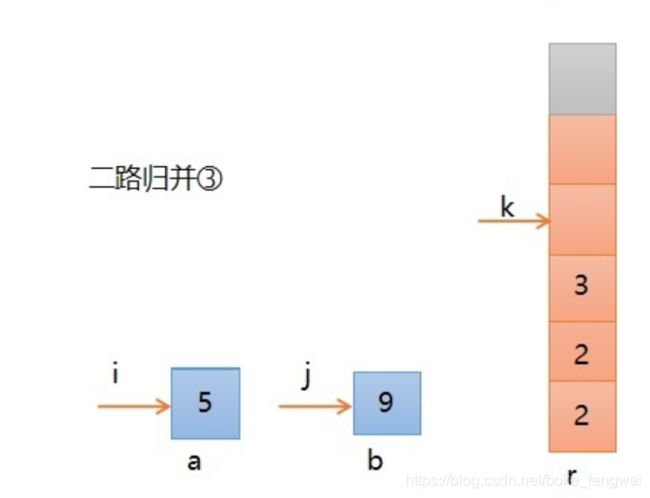
第四步,继续比较,此时a[i]小,所以a的元素5进入r,则如下图所示,i, k分别加1,此时序列a的3个元素已经归并完,b中还剩下一个,这个可以通过k可以看出,它还没有到达个数5。
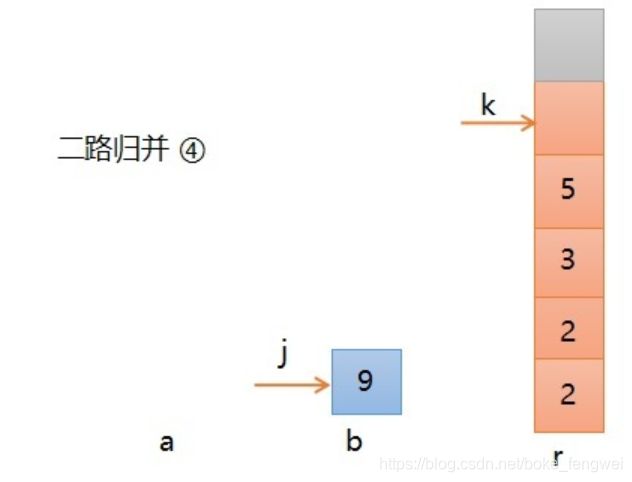
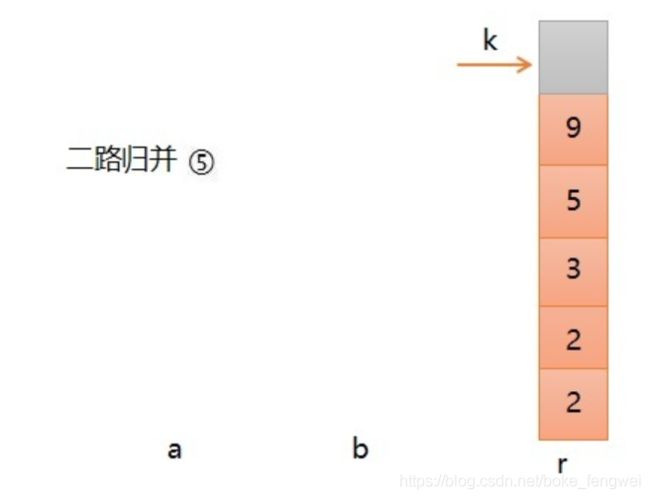
第五步,将序列b中的所有剩余元素直接放入r中即可,不用做任何比较了,直至b变空,二路归并结束。
这其实也就是和我们的第一个图解是一样的思想
完整代码
#include
using namespace std;
void Swap(int arr[], int a, int b){
int temp = arr[a];
arr[a] = arr[b];
arr[b] = temp;
}
void combindArray(int array[], int left, int right, int mid){
//将[left,mid) 和数组[mid,right)进行合并
int* p = new int[right - left];
int i = 0;
int start = left;
int end = right;
int port = mid;
while (left < mid&&port < right){
if (array[left] < array[port]){
p[i++] = array[left++];
}
else{
p[i++] = array[port++];
}
}
while (left < mid){
p[i++] = array[left++];
}
while (port < right){
p[i++] = array[port++];
}
i = 0;
while (start < end){
array[start++] = p[i++];
}
delete[]p;
}
//1.平均切割区间
//2.分治处理左右两个小区间,直到size ==0 或者size ==1
//3.合并左右两个有序数组
void MergeSortInner(int array[], int left, int right){//此时我们的区间是[left,right)
if (left == right){
return;//size=0;
}
if (left + 1 == right){
return;
}
int mid = (left + right) / 2;
MergeSortInner(array, left, mid);
MergeSortInner(array, mid, right);
//合并两个区间的元素
combindArray(array, left, right, mid);
}
//归并排序就是将两个有序的区间进行合并,采用分治算法
void MergeSort(int array[], int size){
MergeSortInner(array, 0, size);
}
void printSort(int array[], int size){
for (int i = 0; i < size; i++){
cout << array[i] << " ";
}
cout << endl;
}
int main(){
int arr[] = { 5, 6, 8, 9, 5, 4, 2, 3, 1, 6 };
int size = sizeof(arr) / sizeof(arr[0]);
MergeSort(arr, size);
printSort(arr, size);
system("pause");
return EXIT_SUCCESS;
}
了解外部排序
数据元素太多不能同时放在内存中,根据排序过程的要求不能在内外存之间移动数据的排序。
比如我们对1000000个数据进行排序,此时内存不够的时候我们就不能进行内部排序,此时应该使用我们的外部排序的思想去进行排序。
外部排序也是指的是大文件的排序,当待排序的文件很大时,无法将整个文件的所有记录同时调入内存进行排序,只能将文件存放在外存,这种排称为外部排序。外部排序的过程主要是依据数据的内外存交换和“内部归并”两者结合起来实现的。
一般来说外排序分为两个步骤:预处理和合并排序。首先,根据可用内存的大小,将外存上含有n个纪录的文件分成若干长度为t的子文件(或段);其次,利用内部排序的方法,对每个子文件的t个纪录进行内部排序。这些经过排序的子文件(段)通常称为顺串(run),顺串生成后即将其写入外存。这样在外存上就得到了m个顺串(m=[n/t])。最后,对这些顺串进行归并,使顺串的长度逐渐增大,直到所有的待排序的记录成为一个顺串为止。
1.预处理阶段
最重要的事情就是选择初始顺串。通常使用的方法为置换选择排序,它是堆排序的一种变形,实现思路同STL的partial_sort。步骤如下:
(1)初始化堆
从磁盘读入M个记录放到数组RAM中;
设置堆末尾标准LAST=M-1;
建立最小值堆。
(2)重复以下步骤直到堆为空
把具有最小关键码值的记录Min也就是根节点送到输出缓冲区;
设R是输入缓冲区中的下一条记录,如果R的关键码大于刚刚输出的关键码值Min,则把R放到根节点,否则使用数组中LAST位置的记录代替根节点,并将刚才的R放入到LAST所在位置,LAST=LAST-1;
(3)重新排列堆,筛出根节点。
如果堆的大小是M,一个顺串的最小长度就是M个记录,因为至少原来在堆中的那些记录将成为顺串的一部分,如果输入时逆序的,那么顺串的长度只能是M,最好情况输入是正序的,有可能一次性就能把整个文件生成一个顺串,由此可见生成顺串的长度是大小不一的,但是每个顺串却是有序的,利用扫雪机模型能够得到平均顺串的长度为2M。
外部排序最常用的算法是多路归并排序,即将原文件分解成多个能够一次性装入内存的部分,分别把每一部分调入内存完成排序。然后,对已经排序的子文件进行归并排序。
2. 二路合并
(1) 二路合并排序
二路合并是最简单的合并方法,合并的实现与内排序中的二路归并算法并无本质区别,下面通过具体例子,分析二路合并外部排序的过程。
有一个含有9000个纪录的文件需要排序(基于关键字)。假定系统仅能提供容纳1800个纪录的内存。文件在外存(如磁盘)上分块存储,每块600个纪录。外部排序的过程分为生成初始顺串和对顺串进行归并排序两个阶段。在生成初始顺串阶段,每次读入1800个纪录(即3段)待内存,采用内排序依次生成顺串依次写入外存储器中。
顺串生成后,就开一开始对顺串进行归并。首先将内存等分成3个缓冲区,和,每个缓冲区可容纳600个纪录,其中和为输入缓冲区,为输出缓冲区,每次从外存读入待归并的块到和,进行内部归并,归并后的结果送入,中的几率写满时再将其写入外存。若(或)中的纪录为空,则将待归并顺串中的后续块读入和(或)中进行归并,直到待归并的两个顺串都已归并为止。重复上述的归并方法,由含有5块(每块上限1800个记录)的顺串经二路归并的一边归并后生成含有3块(每块上限3600个记录)的顺串,再经过第二遍……第s遍(s=[],m为初始顺串的个数),生成含有所有记录的顺串,从而完成了二路归并外部排序。
对文件进行外部排序的过程中,因为对外存的读写操作所用的操作的时间远远超过在内存中产生顺串和合并所需的时间,所以常用对外存的读写操作所用的时间作为外部排序的主要时间开销。分析一下上述二路归并排序的对外存的读写时间。初始时生成5个顺串的读写次数为30次(每块的读写次数为2次)。
类似地,可得到二路、三路……多路合并方法。
(2) 多路替代选择合并排序
采用多路合并技术,可以减少合并遍数,从而减少块读写次数,加快排序速度。但路数的多少依赖于内存容量的限制。此外,多路合并排序的快慢还依赖于内部归并算法的快慢。
设文件有n个纪录,m个初始顺串,采用k路合并方法,那么合并阶段将进行遍合并。k路合并的基本操作是从k个顺换的第一个纪录中选出最小纪录(即关键字最小的纪录),把它从输入缓冲区移入输出缓冲区。若采用直接选择方式选择最小元,需要k-1次比较,遍合并共需n(k-1)=次比较。由于随k的增长而增长,则内部归并时间亦随k的增大而增大,这将抵消由于增大k而减少外存信息读写时间所得的效果。若在k个纪录中采用树形选择方式选择最小元,则选择输出一个最小元之后,只需从某叶到根的路径上重新调整选择树,即可选择下一个最小元。重新构造选择书仅用O()次比较,于是内部合并时间O(n)=O(),它与k无关,不再随k的增大而增大。
常见的有基于“败者树”的多路替代选择合并排序方法。