【数据结构】选择排序(简单选择排序和堆排序)的算法思想和代码实现
目录
1、简单选择排序
1.1 算法思想
1.2 代码实现
1.3 例题分析
2、堆排序
2.1 算法思想
2.2 代码实现
2.3 例题分析
1、简单选择排序
1.1 算法思想
简单选择排序算法是一种基本的排序算法,其思想是在未排序的元素中找到最小的元素,然后将其放到已排序序列的末尾,以此类推,直到所有元素均排序完毕。具体步骤如下:
- 从待排序序列中找到最小的元素;
- 将最小元素放到序列的起始位置;
- 在剩余的未排序元素中找到最小的元素,放到已排序序列的末尾;
- 重复步骤3,直到所有元素均排序完毕。
简单选择排序算法的时间复杂度为 O(n²),空间复杂度为 O(1),是一种不稳定的排序算法。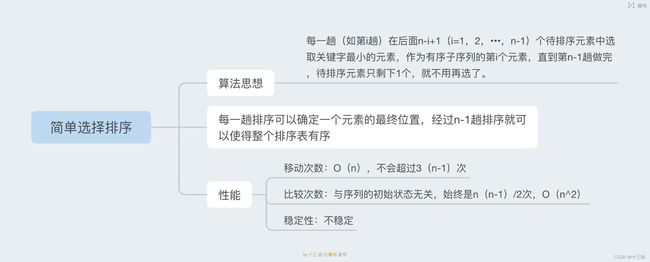
1.2 代码实现
代码的思路:每一次循环从未排序的部分找到最小值的下标,然后将它与未排序部分的第一个元素交换,将最小值插入到已排序部分的末尾。重复这个过程,直到整个数组被排序。
#include
void selection_sort(int arr[], int n) {
int i, j, min_idx;
for (i = 0; i < n - 1; i++) {
min_idx = i;
for (j = i + 1; j < n; j++) {
if (arr[j] < arr[min_idx]) {
min_idx = j;
}
}
int temp = arr[i];
arr[i] = arr[min_idx];
arr[min_idx] = temp;
}
}
int main() {
int arr[] = {64, 34, 25, 12, 22, 11, 90};
int n = sizeof(arr) / sizeof(arr[0]);
selection_sort(arr, n);
printf("Sorted array: \n");
for (int i = 0; i < n; i++) {
printf("%d ", arr[i]);
}
return 0;
}
1.3 例题分析
假设有一个数组[3, 1, 6, 2, 8, 4, 7, 5],使用简单选择排序对其进行排序。
首先,在第一轮排序中,我们从数组中找到最小的元素1,并将其与第一个元素3交换。这个数组现在变成了[1, 3, 6, 2, 8, 4, 7, 5]。
在第二轮排序中,我们从第二个元素开始找到最小的元素2,并将其与第二个元素3交换。这个数组现在变成了[1, 2, 6, 3, 8, 4, 7, 5]。
在第三轮排序中,我们从第三个元素开始找到最小的元素4,并将其与第三个元素6交换。这个数组现在变成了[1, 2, 4, 3, 8, 6, 7, 5]。
在第四轮排序中,我们从第四个元素开始找到最小的元素3,并将其与第四个元素8交换。这个数组现在变成了[1, 2, 4, 3, 3, 6, 7, 5]。
在第五轮排序中,我们从第五个元素开始找到最小的元素3,并将其与第五个元素8交换。这个数组现在变成了[1, 2, 4, 3, 3, 6, 7, 5]。
在第六轮排序中,我们从第六个元素开始找到最小的元素5,并将其与第六个元素6交换。这个数组现在变成了[1, 2, 4, 3, 3, 5, 7, 6]。
在第七轮排序中,我们从第七个元素开始找到最小的元素6,并将其与第七个元素7交换。这个数组现在变成了[1, 2, 4, 3, 3, 5, 6, 7]。
最终结果是排序后的数组[1, 2, 3, 3, 4, 5, 6, 7]。
2、堆排序
2.1 算法思想
堆排序是一种常见的排序算法,它的基本思想是将待排序序列构建成一个大根堆或小根堆,然后将堆顶元素与末尾元素交换,再对剩余元素进行重建堆的操作,直到整个序列有序为止。
具体步骤如下:
1.将待排序序列构建成一个大根堆或小根堆。
2.取出堆顶元素,即最大或最小元素,与末尾元素进行交换。
3.反复执行步骤2,直到整个序列有序为止。
下面是算法的详细过程:
1.将待排序序列构建成一个大根堆或小根堆。
(1)从最后一个非叶子节点开始,自下而上依次调整堆,使得每个节点的值都大于等于(或小于等于)其子节点的值。
(2)重复执行(1)步骤,直到整个序列成为一个大根堆或小根堆。
2.取出堆顶元素,即最大或最小元素,与末尾元素进行交换。
3.对剩余元素进行重建堆的操作,重复执行步骤2和步骤3,直到整个序列有序为止。
堆排序算法的时间复杂度为O(nlogn),空间复杂度为O(1)。其中,构建堆的时间复杂度为O(n),交换元素的时间复杂度为O(logn),总时间复杂度为O(nlogn)。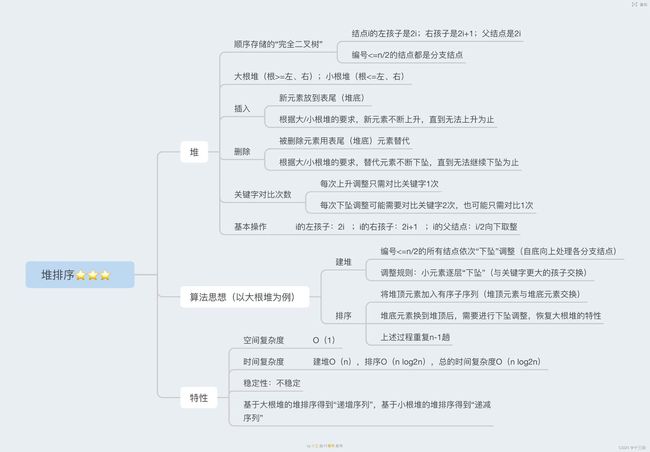
2.2 代码实现
以下是C语言递归实现堆排序代码:
#include
// 交换两个数的值
void swap(int *a, int *b) {
int temp = *a;
*a = *b;
*b = temp;
}
// 将以 root 为根节点的子树调整为大根堆(即保证根节点的值最大)
void adjustMaxHeap(int arr[], int root, int end) {
int leftChild = root * 2 + 1; // 左孩子节点的下标
int rightChild = root * 2 + 2; // 右孩子节点的下标
int maxIdx = root; // 记录最大值的下标
if (leftChild <= end && arr[leftChild] > arr[maxIdx]) {
maxIdx = leftChild;
}
if (rightChild <= end && arr[rightChild] > arr[maxIdx]) {
maxIdx = rightChild;
}
if (maxIdx != root) {
swap(&arr[root], &arr[maxIdx]);
adjustMaxHeap(arr, maxIdx, end); // 递归调整子树
}
}
// 堆排序递归实现函数
void heapSortRecursion(int arr[], int start, int end) {
if (start >= end) { // 当子序列长度为1时,递归结束
return;
}
// 构建大根堆(从最后一个非叶子节点开始,向前依次调整每个子树)
for (int i = (end - 1) / 2; i >= start; i--) {
adjustMaxHeap(arr, i, end);
}
// 将堆顶元素(最大值)与序列末尾元素交换,并缩小堆的范围
swap(&arr[start], &arr[end]);
end--;
// 递归排序子序列
heapSortRecursion(arr, start, end);
}
int main() {
int arr[] = { 4, 3, 6, 9, 1, 2, 5, 8, 7 };
int len = sizeof(arr) / sizeof(arr[0]);
heapSortRecursion(arr, 0, len - 1);
for (int i = 0; i < len; i++) {
printf("%d ", arr[i]);
}
return 0;
}
在这个实现中,主要分为三个函数:
swap函数用于交换两个数的值;adjustMaxHeap函数用于将以某个节点为根节点的子树调整为大根堆;heapSortRecursion函数是递归实现的堆排序函数。
其中,在 heapSortRecursion 函数中,首先进行了堆的构建,即从最后一个非叶子节点开始,向前依次调整每个子树,保证每个子树都是大根堆。接着将堆顶元素(即最大值)与序列末尾元素交换,并缩小堆的范围。最后,递归地将子序列排序,直到子序列长度为1时递归结束。
2.3 例题分析
假设有以下一组数据:5, 3, 6, 2, 1, 9, 4, 8, 7。
- 首先将这组数据构建成一个大根堆,过程如下:
- 从底部开始,将树中的每个子树都调整为大根堆。
- 第一次调整后,得到以下结果:5, 3, 9, 2, 1, 6, 4, 8, 7。
- 第二次调整后,得到以下结果:5, 3, 9, 8, 1, 6, 4, 2, 7。
- 第三次调整后,得到以下结果:9, 3, 5, 8, 1, 6, 4, 2, 7。
- 第四次调整后,得到以下结果:9, 8, 5, 3, 1, 6, 4, 2, 7。
- 第五次调整后,得到以下结果:9, 8, 6, 3, 1, 5, 4, 2, 7。
- 第六次调整后,得到以下结果:9, 8, 6, 3, 1, 5, 4, 2, 7。
- 第七次调整后,得到以下结果:9, 8, 7, 3, 1, 5, 4, 2, 6。
-
将堆顶元素9和堆末元素7交换位置,得到以下结果:7, 8, 6, 3, 1, 5, 4, 2, 9。
-
将除去已经有序的堆末元素7之外的剩余元素重新构建成一个新的大根堆,得到以下结果:8, 3, 6, 2, 1, 5, 4, 7。
-
重复步骤2和3,直到所有元素都有序。最终结果为:1, 2, 3, 4, 5, 6, 7, 8, 9。