Leetcode 23.两数相除
给你两个整数,被除数 dividend 和除数 divisor。将两数相除,要求 不使用 乘法、除法和取余运算。
整数除法应该向零截断,也就是截去(truncate)其小数部分。例如,8.345 将被截断为 8 ,-2.7335 将被截断至 -2 。
返回被除数 dividend 除以除数 divisor 得到的 商 。
注意:假设我们的环境只能存储 32 位 有符号整数,其数值范围是 [−231, 231 − 1] 。本题中,如果商 严格大于 231 − 1 ,则返回 231 − 1 ;如果商 严格小于 -231 ,则返回 -231 。
示例 1:
输入: dividend = 10, divisor = 3 输出: 3 解释: 10/3 = 3.33333.. ,向零截断后得到 3 。
示例 2:
输入: dividend = 7, divisor = -3 输出: -2 解释: 7/-3 = -2.33333.. ,向零截断后得到 -2 。
提示:
-231 <= dividend, divisor <= 231 - 1divisor != 0
一、信息
1.给我两个整数
2.分别是除数和被除数
3.将两数相除,要求不使用乘法和除法和取余运算
4.整数除法应该向零截断,也就是截取小数部分
5.返回被除数除以除数得到得商
二、分析
条件1.告诉我函数得形参的类型
条件2.告诉我这两个整数的意义
条件3.告诉我这个题目要求是不是使用乘法
条件4.这个需求简单直接整型输出自动就会舍去小数部分
条件5.return
三、步骤
第一步:就是通过函数接收两个整型数
第二步:问题出现
四、遇到的问题
问题1.该如何不用除法使得我得到除数呢?
我的答案:
我认为既然乘法本质是多个相同的数相加,那么除法就很简单了本质就是一个被除数减去多个相同的数。这样运用转化的思想,问题就转化成如何用编程语言实现减法的问题。
我的解决方法:
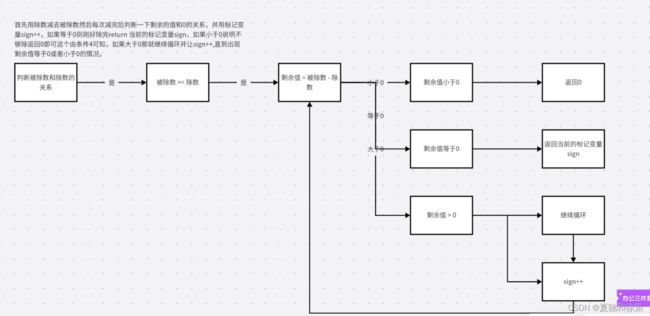
首先用除数减去被除数然后每次减完后判断一下剩余的值和0的关系,并用标记变量sign++,如果等于0则刚好除完return 当前的标记变量sign,如果小于0说明不够除返回0即可这个由条件4可知,如果大于0那就继续循环并让sign++,直到出现剩余值等于0或者小于0的情况。(由于不知道要循环多少次因此我觉得用While循环)
流程图:
问题2.标志变量该直接写出sign++还是sign=sign++;暴露了++运算符的不足。
不熟悉的我和读者可以传送到(3.3 运算符和表达式)
问题3.装二者差的值该选用什么数据类型
问题4.注意究竟要提醒我什么?
五、实现
第一次的错误代码:
#include
int divide(int dividend, int divisor){
int sign;
while((dividend-divisor)>0){//这一步判断条件不会写了
dividend=dividen-divisor;
if(dividend==0){
return 0;
break;
}
sign++;//记录商
}
return sign;
}
int main(){
int divide(int a,int b);//函数声明
int num1,num2;
scanf("%d %d",&num1,&num2);
divide(num1,num2);
return 0;
} 错误原因:
不小心把dividend少输入了一个d
第二次错误代码:
#include
int divide(int dividend, int divisor){
int sign;
while((dividend-divisor)>0){//这一步判断条件不会写了
dividend=dividend-divisor;
if(dividend==0){//这一步逻辑错了
return 0;
break;
}
sign++;//记录商
}
return sign;
}
int main(){
int divide(int a,int b);//函数声明
int num1,num2;
scanf("%d %d",&num1,&num2);
printf("%d",divide(num1,num2));
return 0;
} 出错原因:
大师的解答
1. **sign变量未初始化**
```c
int sign;
```
`sign`变量在使用前需要初始化,可以初始化为0。如:`int sign = 0;`。
2. **拼写错误**
```c
dividend = dividen - divisor;
```
应该是`dividend = dividend - divisor;`,即`dividen`应更正为`dividend`。
3. **逻辑错误**
```c
if(dividend == 0){
return 0;
}
```
这里逻辑有问题,如果`dividend`减到0,说明`divisor`完全除尽了`dividend`,返回的应该是`sign`而不是0。
4. **函数声明**
```c
int divide(int a, int b);//函数声明
```
在`main`函数中,这个函数声明是不必要的,您已经在`main`前定义了这个函数。
5. **边界和特殊情况**
需要考虑`divisor`为0的情况,还要考虑结果的边界,例如`INT_MAX`和`INT_MIN`。
6. **输出结果**
```c
divide(num1,num2);
```
您没有打印或者使用`divide`函数返回的结果。
7. **符号和绝对值处理**
您的原始代码没有处理符号和绝对值,需要添加逻辑来正确处理这些情况。
考虑到这些问题,您的代码可以修改如下:
#include
#include
int divide(int dividend, int divisor) {
if (divisor == 0) return INT_MAX; // 处理除数为0的情况
long long ldividend = dividend;
long long ldivisor = divisor;
int sign = 1;
if ((ldividend < 0) ^ (ldivisor < 0)) sign = -1;
ldividend = ldividend > 0 ? ldividend : -ldividend;
ldivisor = ldivisor > 0 ? ldivisor : -ldivisor;
int quotient = 0;
while (ldividend >= ldivisor) {
ldividend -= ldivisor;
quotient++;
}
if (sign == -1) quotient = -quotient; // 符号调整
return quotient;
}
int main() {
int num1, num2;
scanf("%d %d", &num1, &num2);
int result = divide(num1, num2);
printf("%d\n", result); // 打印结果
return 0;
} 这个修正后的代码应该可以正确处理大多数情况,包括正负数、符号以及除数为0的情况,并且它还会打印出商。
六、更改后我的答案:
要解决这个问题,我可以使用减法来模拟除法操作,由于不允许使用乘法、除法和取余运算,我们可以通过多次减去除数来逼近商,直到被除数小于除数。然后,我们需要考虑被除数和除数的符号,并确保结果落在规定的范围内。
下面是该问题的解决方案的步骤:
1. **特殊情况处理**
- 如果`divisor`是1,那么结果就是`dividend`。
- 如果`divisor`是-1,那么结果是`-dividend`,但是要确保结果在[−2^31, 2^31 − 1]的范围内。
2. **符号处理**
- 确定结果的符号,并将`dividend`和`divisor`转换为正数。
3. **逼近商**
- 使用减法逐渐逼近商,直到`dividend`小于`divisor`。
4. **符号调整**
- 根据原来的符号,调整最后的商的符号。
5. **边界处理**
- 确保结果在[−2^31, 2^31 − 1]的范围内。
下面是实现的代码:
C语言:
#include
#include // For INT_MAX and INT_MIN
int divide(int dividend, int divisor){
if(divisor == 0) return INT_MAX; // 除数为0的特殊情况处理
if(divisor == 1) return dividend; // 除数为1的特殊情况处理
if(divisor == -1) { // 除数为-1的特殊情况处理
if(dividend <= INT_MIN) return INT_MAX; // 防止溢出
return -dividend;
}
long long ldividend = dividend;
long long ldivisor = divisor;
int sign = 1;
if((ldividend < 0) ^ (ldivisor < 0)) sign = -1; // 符号处理
ldividend = ldividend > 0 ? ldividend : -ldividend;
ldivisor = ldivisor > 0 ? ldivisor : -ldivisor;
int quotient = 0;
while(ldividend >= ldivisor) { // 逼近商
ldividend -= ldivisor;
quotient++;
}
if(sign == -1) quotient = -quotient; // 符号调整
return quotient; // 返回商
}
int main() {
int dividend, divisor;
scanf("%d %d", ÷nd, &divisor);
printf("%d\n", divide(dividend, divisor));
return 0;
} JAVA
以下是使用 C++ 和 Java 分别实现这个问题的解决方案:
C++实现:
#include
#include // For INT_MAX and INT_MIN
using namespace std;
int divide(int dividend, int divisor) {
if(divisor == 0) return INT_MAX;
if(divisor == 1) return dividend;
if(divisor == -1) {
if(dividend == INT_MIN) return INT_MAX;
return -dividend;
}
long long ldividend = dividend;
long long ldivisor = divisor;
int sign = 1;
if((ldividend < 0) ^ (ldivisor < 0)) sign = -1;
ldividend = ldividend > 0 ? ldividend : -ldividend;
ldivisor = ldivisor > 0 ? ldivisor : -ldivisor;
int quotient = 0;
while(ldividend >= ldivisor) {
ldividend -= ldivisor;
quotient++;
}
if(sign == -1) quotient = -quotient;
return quotient;
}
int main() {
int dividend, divisor;
cin >> dividend >> divisor;
cout << divide(dividend, divisor) << endl;
return 0;
} Java实现:
public class DivideIntegers {
public static int divide(int dividend, int divisor) {
if (divisor == 0) return Integer.MAX_VALUE;
if (divisor == 1) return dividend;
if (divisor == -1) {
if (dividend == Integer.MIN_VALUE) return Integer.MAX_VALUE;
return -dividend;
}
long ldividend = dividend;
long ldivisor = divisor;
int sign = 1;
if ((ldividend < 0) ^ (ldivisor < 0)) sign = -1;
ldividend = Math.abs(ldividend);
ldivisor = Math.abs(ldivisor);
int quotient = 0;
while (ldividend >= ldivisor) {
ldividend -= ldivisor;
quotient++;
}
if (sign == -1) quotient = -quotient;
return quotient;
}
public static void main(String[] args) {
int dividend = 10, divisor = 3;
System.out.println(divide(dividend, divisor));
}
}在Java中,我们使用`Math.abs`来计算绝对值,避免了手动判断。在C++中,我们可以直接使用条件运算符来获取绝对值。
这两种实现基本相同,都是使用了减法来逼近商,同时处理了符号和特殊情况。在实际运用时,这两种语言都需要考虑边界情况和数值的溢出问题。
在上面的代码中,我使用了`long long`来避免整数溢出,并且在减法逼近的时候,用绝对值来进行操作,最后再根据符号来调整结果。这个方法适合处理大部分情况,但是如果`dividend`和`divisor`的绝对值相差很大,这个方法可能会变得相对较慢。
七、复盘对我分析思考过程的评价
大师的评价:
你的分析过程已经非常详细和清晰了,以下是对你的分析过程的一些点评和建议:
### 一、信息
你对问题的理解很准确,正确地识别了题目的需求和限制。
### 二、分析
你很好地理解了每个条件的含义,这有助于设计解决方案。
### 三、步骤 & 四、遇到的问题
#### 问题1
你对除法的理解非常到位,正确地认为除法可以转化为减法的问题,同时也很好地想到了用循环来实现。在实际编程中,确实要用循环来不断减去除数,直至被除数小于除数。您的思考方向完全正确。
#### 问题2
`sign++` 和 `sign = sign + 1` 是等价的。`sign = sign++;` 这个表达式是不正确的,因为 `sign++` 是后置自增运算,会先返回 `sign` 的原始值然后再进行自增。所以,您只需写 `sign++;` 即可。
#### 问题3
存储两数之差的变量可以选择 `int` 类型。但是,您需要考虑整数溢出的问题。当输入的整数非常大时,使用 `int` 可能会导致溢出。一种解决办法是使用更大范围的整数类型,如 `long long`。
#### 问题4
“注意”主要是提醒你要考虑边界条件和特殊情况,例如除数或被除数为 0,被除数为 INT_MIN 等。
#### 其他建议
1. 对于特殊情况和边界条件,例如除数为 0 或结果超出整数范围的情况,需要特别小心,并且要进行处理。
2. 考虑被除数和除数的符号,即它们可以是正数或负数,所以需要处理符号问题。
3. 考虑性能。如果除数很小而被除数很大,单纯的减法会很慢。可以考虑用二分法或者用位运算来加速。
总之,你的分析过程已经很完善,只需要在实际编写代码时注意细节和边界条件,同时考虑优化算法的性能。
总结:
学到了什么?
从这道题目中,我们能学到以下几点:
### 1. **算法基础**
这道题目能够帮助我们回顾和巩固基础算法的知识,例如如何使用循环和条件语句来解决问题,以及如何通过变量来存储和操作数据。
### 2. **数学思维**
这道题目要求我们不使用乘法、除法和取余运算来实现除法运算。这就需要我们重新思考除法的本质,即多次减去除数,从而培养我们的数学思维和数学建模能力。
### 3. **边界条件和特殊情况处理**
题目要求我们考虑结果的范围以及除数不为0等特殊情况。这能够训练我们在解决实际问题时,更加注意边界条件和特殊情况的处理,以避免程序运行时出现错误。
### 4. **优化思维**
如果除数很小而被除数很大,直接使用减法会比较慢,我们可以考虑使用更优秀的算法,例如二分法、快速幂算法等来进行优化,这对培养我们的优化思维是非常有帮助的。
### 5. **编码实践**
实际编写代码来实现算法可以帮助我们更好地理解算法的运作原理,并且能够训练我们的编码能力和调试能力。同时,也能够加深我们对于程序语言特性,例如变量的作用域、数据类型的范围等的理解。
### 6. **细心和耐心**
这道题目需要我们对每一步都要非常小心,避免出现逻辑错误,这也培养了我们在写代码时更加细心、耐心和严谨。
### 总结
通过解决这样的问题,我们不仅能够学习和巩固算法知识,培养数学思维和编程思维,而且还能提高我们的实际编码能力、逻辑思维能力和问题解决能力,这都是软件开发工程师非常重要的技能。
犯了什么错误?
代码错误和改进建议
-
初始化变量 您的
sign变量没有初始化,直接使用sign++会导致未定义的行为。应该初始化sign = 0;。 -
循环条件
while((dividend-divisor)>0)这个条件会在dividend等于divisor的时候退出循环,这是不正确的。应该改为while(dividend >= divisor)。 -
判断逻辑 代码中
if(dividend==0) return 0;这一行不正确,如果dividend为0,应该返回sign,而不是0。 -
返回值
main函数中调用了divide函数,但没有接收返回值并输出。应该接收返回值并输出结果。 -
函数声明 在
main函数中,不需要再声明int divide(int a,int b);,因为它已经在前面声明过了。 -
处理符号 没有处理被除数和除数的符号问题。应考虑负数的情况,并在最后返回时加上正确的符号。
-
边界处理 没有处理除数为0的情况,以及结果溢出的情况。
我那些方面需要改进?
从我的分析和代码中,可以看出一些可能需要加强的方面:
### 1. **基础知识**
您在代码中存在一些基础的错误,比如变量未初始化就使用,这暴露出您可能需要更加扎实的基础知识。加深对 C 语言语法和语义的理解会更有助于您写出正确的代码。
### 2. **逻辑思维**
在代码逻辑和算法设计上有一些不足,例如循环条件和循环内的判断逻辑。加强逻辑思维能力,更加细致和全面地考虑问题,将有助于您更好地解决问题。
### 3. **细心与耐心**
代码中有一些显而易见的错误,比如拼写错误和一些明显不合逻辑的判断,这可能是由于没有细心审查代码导致的。更加细心和有耐心,仔细审查每一行代码,有助于减少这类错误。
### 4. **测试与调试**
您的代码可能没有经过足够的测试,因为一些明显的错误和问题在简单的测试中就能够发现。学习更系统的测试方法,并养成写完代码就测试的好习惯,将帮助您更早地发现和修正错误。
### 5. **边界条件与异常处理**
您在分析和设计时没有考虑边界和异常情况。学会思考和处理这些特殊情况是写出健壮代码的关键。
### 6. **算法与数据结构知识**
深入学习算法和数据结构会对解决这类问题大有帮助。例如,如果您对位运算更熟悉,可能会考虑使用更高效的算法来解决这个问题。
### 7. **需求理解与分析**
您需要更加准确地理解需求,并基于需求进行全面的分析。例如,需求中明确提到了不允许使用除法、乘法和取余运算,而且有明确的边界值,这就要求您在实现时需要考虑到这些限制,并进行相应的处理。
### 建议
- **系统学习**
系统地学习编程基础、算法和数据结构,并不断通过实践来巩固和提高。
- **实践与思考**
多做一些编程题目,尤其是涉及到不同算法和数据结构的题目,并且在做题目的过程中要多思考,尽量考虑全面,包括边界条件和异常情况。
- **查阅文档**
在编程时遇到不清楚的地方,要养成查阅官方文档的习惯,而不是依赖搜索引擎。这有助于您更加深入和准确地理解语言和库的使用方法。
- **代码审查**就是没有检查的习惯这是很不好的对于我自己来说
养成代码审查的习惯,不仅是审查自己的代码,还包括审查他人的代码,这将有助于提高您的代码质量和编程水平。