数据结构之并查集
在此之前我们需要思考:并查集是解决什么问题的,如何应用?
并查集解决的是连通性(无向图联通分量)和传递性(家谱关系)问题,并且可以动态的维护。抛开格子不看,任意一个图中,增加一条边形成环当且仅当这条边连接的两点已经联通,于是可以将点分为若干个集合,每个集合对应图中的一个连通块。
Acwing1250 格子合并;
Alice和Bob玩了一个古老的游戏:首先画一个 n×nn×n 的点阵(下图 n=3n=3 )。
接着,他们两个轮流在相邻的点之间画上红边和蓝边:
直到围成一个封闭的圈(面积不必为 1)为止,“封圈”的那个人就是赢家。因为棋盘实在是太大了,他们的游戏实在是太长了!
他们甚至在游戏中都不知道谁赢得了游戏。
于是请你写一个程序,帮助他们计算他们是否结束了游戏?
输入格式
输入数据第一行为两个整数 n 和 m。n表示点阵的大小,m 表示一共画了 m 条线。
以后 mm 行,每行首先有两个数字(x,y),代表了画线的起点坐标,接着用空格隔开一个字符,假如字符是 D,则是向下连一条边,如果是 R 就是向右连一条边。
输入数据不会有重复的边且保证正确。
输出格式
输出一行:在第几步的时候结束。
假如 m 步之后也没有结束,则输出一行“draw”。
数据范围
1≤n≤200,
1≤m≤24000
思路: 二维坐标一维化,用并查集判断是否能为成封闭图形
y总说还可以用tarjin本弱狗不会啊~~~。
#include
using namespace std;
typedef long long ll;
const int N=40010;
int p[N];
int n,m;
int get(int x,int y)
{
return x*n+y;
}
int find(int x)
{
if(p[x]!=x) p[x]=find(p[x]);
return p[x];
}
int main(){
cin>>n>>m;
for(int i=0;i>x>>y>>d;
x--,y--;
int a=get(x,y);
int b=0;
if(d=='D') b=get(x+1,y);
else b=get(x,y+1);
int pa=find(a), pb=find(b);
if(pa==pb)
{
ans=i;
break;
}
p[pa]=pb;
}
if(ans)cout< 补加例题:
蓝桥杯选拔赛
Problem:C
Time Limit:1000ms
Memory Limit:65535K
Description
小蓝经常在各种花园中散步。 这些花园由 N 个亭子以及 M 条将这些亭子连接起来的道路。 然而他经常在一些花园中迷路。 如果一个花园中包含一条起点和终点相同且不经过相同道路的非空路径, 那么小蓝就会在该花园中迷路。 现在给定一个花园的亭子及相应的道路, 请问小蓝会在该花园中迷路吗?
Input
输入第一行包含两个整数 N 和M , 表示花园的亭子数目和道路数目。 接下来包含 M 行,每行包含2个整数A和B , 表示有一条连接着第 A 亭子和第B 亭子的道路。
Output
输出一行。 如果小蓝在该亭子中会迷路,那么输出 "Yes", 否则输出 "No" (输出不包含引号)。
Sample Input
5 7 3 1 1 2 2 3 5 3 2 4 5 2 3 4
Sample Output
Yes
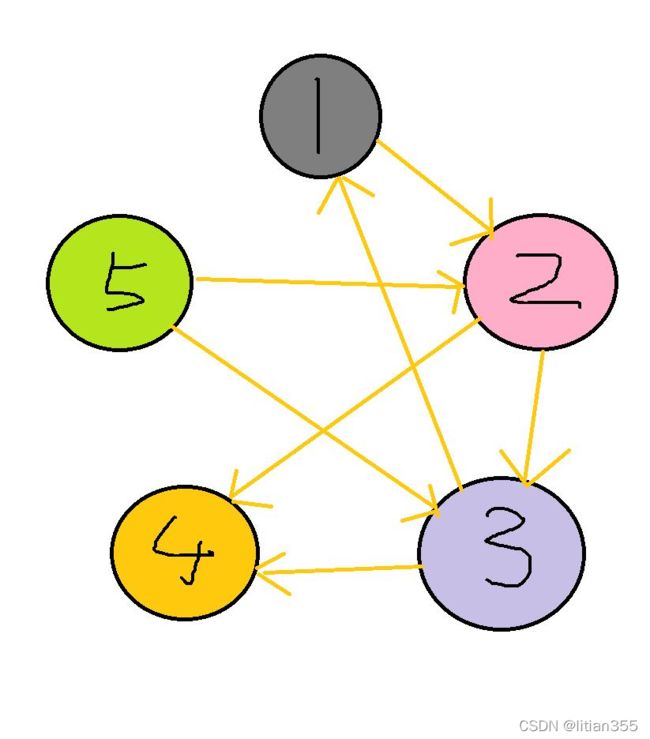
根据例一数据用并查集生成的有向图
Hint
例子2: 5 3 1 2 2 3 4 5 No
Source
和上面题可以说是一模一样了,关键是理解 :如果一个花园中包含一条起点和终点相同且不经过相同道路的非空路径, 意思就是能构成闭环,描述的还是不太直接。
#include
using namespace std;
const int N=1e5+10;
int n,m;
int p[N];
int find(int x)
{
if(p[x]!=x) p[x]=find(p[x]);
return p[x];
}
int main(){
cin>>n>>m;
int f=0;
for(int i=1;i<=n;i++) p[i]=i;
for(int i=0;i>a>>b;
int pa=find(a),pb=find(b);
if(pa==pb)
{
f=1;
}
p[pa]=pb;
}
if(f) cout<<"Yes"<