动态规划:两个数组的dp问题(C++)
动态规划:两个数组的dp问题
-
- 前言
- 两个数组的dp问题
-
- 1.最长公共子序列(中等)
- 2.不同的子序列(困难)
- 3.通配符匹配(困难)
- 4.正则表达式(困难)
- 5.交错字符串(中等)
- 6.两个字符串的最小ASCII删除和(中等)
- 7.最长重复子数组(中等)
前言
动态规划往期文章:
- 动态规划入门:斐波那契数列模型以及多状态
- 动态规划:路径和子数组问题
- 动态规划:子序列问题
- 动态规划:回文串问题
两个数组的dp问题
1.最长公共子序列(中等)
链接:最长公共子序列
-
状态表示
对于两个数组的dp,采用一维dp是没有办法清晰的表示状态的,故对于两个数组的dp我们通常采用二维数组。
故定义状态表示为dp[i] [j]:s1的[0,i]区间和s2的[0,j]区间之间的最长公共子序列。 -
状态转移方程
对s1的[0,i]区间和s2的[0,j]区间,我们分情况讨论:
(1)s1[i] == s2[j],我们只需要知道s1的[0,i - 1]区间和s2的[0,j - 1]区间之间的最长公共子序列,然后加一即可,即dp[i] [j] = dp[i - 1] [j - 1] + 1。(比如s1 = "abc"和s2 = “akc”,就是"ab"和"ak"的最长公共子序列加1)
(2)s1[i] != s2[j],这个这时最长公共子序列⼀定不会同时以s1[i]和s2[j]结尾。
①有可能以s2[j]结尾,去s1的 [0, i - 1]以及s2的 [0, j] 区间内找:此时最大长度为dp[i - 1] [j]。(比如s1 = “ack”,s2 = “bc”)
②有可能以s1[i]结尾,去s1的[0, i]以及s2的 [0, j - 1] 区间内找:此时最大长度为dp[i] [j - 1]。(比如s1 = “ac”,s2 = “cb”)
③也有可能两者都不是结尾,但这个情况是包括在前两个情况中的,一定小于等于前两者。(比如s1 = “acd”,s2 = “aca”)
故对于(2)情况,dp[i] [j] = max(dp[i - 1] [j], dp[i] [j - 1])。 -
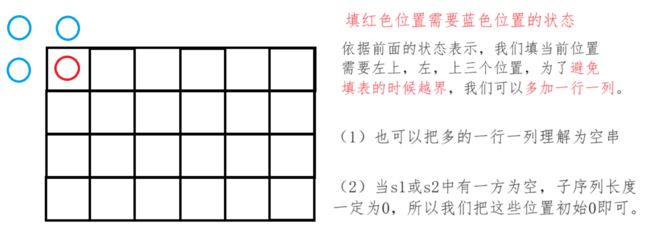
初始化
-
填表顺序
参照上面的图,填表顺序为行从上到下,每一行从左到右。 -
返回值
依据状态表示,返回值为dp[m] [n](m,n分别为s1、s2长度)。
- 代码实现
class Solution {
public:
int longestCommonSubsequence(string s1, string s2) {
int m = s1.size(), n = s2.size();
vector<vector<int>> dp(m + 1, vector<int>(n + 1));
//处理下标映射
s1 = " " + s1, s2 = " " + s2;
for(int i = 1; i <= m; i++)
for(int j = 1; j <= n; j++)
{
if(s1[i] == s2[j])
dp[i][j] = dp[i - 1][j - 1] + 1;
else
dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
}
return dp[m][n];
}
};
2.不同的子序列(困难)
链接:不同的子序列
-
状态表示
这个题目虽然标的是困难,但是有前面的做题经验其实还好。
对这种问题,我们采用二维表,定义状态表示为dp[i] [j]:t的[0, j]区间在s的[0, i]区间出现的方案个数。 -
状态转移方程
对s的[0,i]区间和t的[0,j]区间,我们分情况讨论:
(1)s[i] == t[j]:
①比如t = "rab"和s = “rabcb”,第一种同时选s[i]、t[j]为结尾,这个时候的方案数为t的[0, j - 1]区间在s的[0, i - 1]区间出现的方案数(ra在rabc中出现的次数),即dp[i - 1] [j - 1]。
②第二种是不同时选s[i]、t[j]为结尾,这个时候的方案数为t的[0, j]区间在s的[0, i - 1]区间出现的方案数(t = "rab"在s的"rabc"中出现的次数),即dp[i - 1] [j]。
两种都符合要求:故(1)情况dp[i] [j] = dp[i - 1] [j] + dp[i - 1] [j - 1]
(2)s[i] != t[j]:
这个时候只有一种选择,即(1)的②情况,故(2)情况dp[i] [j] = dp[i - 1] [j] 。 -
初始化
这个题目的初始化和上一题相似,多开一行一列,把多的一行一列当作空串。其中当t为空串时在s中一定有一种方案(s也拿一个空串出来),故初始化第一列为1。 -
填表顺序
填表不明白参考第一题,填表顺序为行从上到下,每一行从左到右。 -
返回值
依据状态表示,返回值为dp[m] [n](m,n分别为s、t长度)。
- 代码实现
class Solution {
public:
int numDistinct(string s, string t) {
int m = s.size(), n = t.size();
//这个题目中间填表的时候会溢出,而且溢的不是一点点
//不过溢出的部分不影响结果,用uint即可
vector<vector<unsigned int>> dp(m + 1, vector<unsigned int>(n + 1));
s = " " + s, t = " " + t; //处理下标映射
for(int i = 0; i < m; i++) dp[i][0] = 1;
for(int i = 1; i <= m; i++)
for(int j = 1; j <= n; j++)
{
dp[i][j] = dp[i - 1][j];
if(s[i] == t[j]) //s[i] == t[j]会多一种选择
dp[i][j] += dp[i - 1][j - 1];
}
return dp[m][n];
}
};
3.通配符匹配(困难)
链接:通配符匹配
-
状态表示
依据前面的做题经验,我们定义一个二维表,定义状态表示为dp[i] [j]:p的[0, j]区间能否匹配s的[0, i]区间。 -
状态转移方程
对s的[0,i]区间和p的[0,j]区间,我们分情况讨论:
(1)s[i] == p[j]或者p[j] == '?'时,dp[i] [j] = dp[i - 1] [j - 1],即只要p的[j - 1]区域能和s的[i - 1]区域匹配,p的[0, j]就可以和s的[0, i]匹配。(比如s = “abc”,p = “ab?”)
(2)p[j] == ’ * ’ 的情况,这个时候有三种可能使得p[0, j]和s[0, i]匹配:
①p的[0, j]可以和s的[0, i - 1]匹配,p[j] == ’ * ’ 在表示原来的字符串基础上加上s[i]即可,即dp[i - 1] [j]为真dp[i] [j]为真。(比如s = “abc”,p = “a*”,"ab"和"a*"是匹配的)
②p的[0, j - 1]可以和s的[0, i]匹配, ’ * ’ 这个时候匹配空串即可,即dp[i] [j - 1]为真dp[i] [j]为真。(比如s = “ab”,p = “ab*”)
③p[0, j - 1]匹配和s的[0, i - 1],p[j] == ’ * ’ 去替换s[i],但这种情况实际是可以被归于第一种情况的,如果s[0, i - 1]和p[0, j - 1]匹配,那么s[0, i - 1]和p[0 , j]也一定会匹配,这个时候 ’ * ’ 做空字符串,即dp[i - 1] [j - 1]为真 == dp[i - 1] [j]为真。
以上情况只要一个为真dp[i] [j]就为真。 -
初始化
和前面一样,为了避免越界以及方便初始化,我们引入空串的概念,多开一行和一列。
①其中两者都为空串可匹配,即dp[0] [0] = true。
②s为空串,p不为空串(第一行除去[0, 0])的时候如果p的[0, j]区间为连续的 ’ * ’ 也是可以匹配空串的,dp[0] [0……j] = true。([0, j]区间表示连续的 ’ * ’ )
③p为空串,s不为空串(第一列除去[0, 0]),这个时候不可能匹配,第一列除开[0][0]其它都初始化为false。 -
填表顺序
填表不明白参考第一题,填表顺序为行从上到下,每一行从左到右。 -
返回值
依据状态表示,返回值为dp[m] [n](m,n分别为s、p长度)。
- 代码实现
class Solution {
public:
bool isMatch(string s, string p) {
int m = s.size(), n = p.size();
s = " " + s, p = " " + p; //处理下标映射
//dp[i][j]:p的[0, j]区间能否匹配s的[0, i]区间
vector<vector<bool>> dp(m + 1, vector<bool>(n + 1));
dp[0][0] = true;
for(int j = 1; j <=n; j++) //初始化s为空串,p有连续'*'可匹配的情况
{
if(p[j] == '*')
dp[0][j] = true;
else
break; //出现非'*'直接结束循环,后面不可能匹配了
}
for(int i = 1; i <= m; i++)
for(int j = 1; j <= n; j++)
{
if(p[j] == '*')
dp[i][j] = dp[i - 1][j] || dp[i][j - 1];
else if(s[i] == p[j] || p[j] == '?')
dp[i][j] = dp[i - 1][j - 1];
}
return dp[m][n];
}
};
4.正则表达式(困难)
链接:正则表达式
-
状态表示
有前面的做题经验,我们定义一个二维表,定义状态表示为dp[i] [j]:p的[0, j]区域能否匹配s的[0, i]区域。 -
状态转移方程
这个题目的重点:"a*"说明这个部分可以出现多次,也可以出现0次,即a表示空串,所以分析的时候应该把"字符 + "当作一个整体来考虑。
对s的[0,i]区间和p的[0,j]区间,我们分情况讨论:
(1)s[i] == p[j]或p[j] == ’ . ’ ,只需要p的[0, j - 1]和s的[0, i - 1]匹配即可,即dp[i - 1] [j - 1]为真dp[i] [j]就为真。(比如s = "abc"和p = “ab.”)
(2)p[j] == ’ * ’ 的情况,这个时候有三种可能使得p[0, j]和s[0, i]匹配:
①p[0, j - 2]和s[0, i]匹配,后面的"字符+"表示空串。即dp[i] [j - 2]为真dp[i] [j]就为真。(比如s = “abc”,p = “abcg*”,p后面的"g*"可以直接作空串)
②p[0, j]和s[0, i - 1]匹配,原本的"字符+"需要多表示一个字符。
但这里多表示的字符是固定的,也就是说必须满足p[j - 1] == s[i] 或 p[j - 1] == ’ . ’ ,这个多表示的字符才能符合要求。即满足前面条件dp[i - 1] [j]为真dp[i] [j]就为真。
(比如s = “abbb”,p = “ab*”,其中"ab*"是可以匹配"abb"的,刚好"b*"多表示一个’ b ’ 符合匹配要求。如果s = "abbc"就p就无法匹配s了)
以上情况只要一个为真dp[i] [j]就为真。 -
初始化
为了避免越界已经方便初始化,我们引入空串的概念,多开一行一列。
①其中两者都为空串可匹配,即dp[0] [0] = true。
②当s为空串,p不为空串(第一行除去[0, 0])的时候如果p为连续的"字符 + * + 字符 + * ……",让这些"字符+ *"全都作空串,是可以匹配s的。即dp[0] [j] = true(j = 2; j <= n; j += 2)。
③p为空串,s不为空串(第一列除去[0, 0]),这个时候不可能匹配,第一列除开[0] [0]其它都初始化为false。 -
填表顺序
填表不明白参考第一题,填表顺序为行从上到下,每一行从左到右。 -
返回值
依据状态表示,返回值为dp[m] [n](m,n分别为s、p长度)。
- 代码实现
class Solution {
public:
bool isMatch(string s, string p) {
int m = s.size(), n = p.size();
//处理下标映射
s = " " + s, p = " " + p;
//dp[i][j]:p的[0,j]区域能否和s的[0,i]区域匹配
vector<vector<bool>> dp(m + 1, vector<bool>(n + 1));
dp[0][0] = 1; //空串可以匹配空串
for(int j = 2; j <= n; j += 2) //s为空串时p为连续的"字符 + *"是可以匹配的
{
if(p[j] == '*')
dp[0][j] = true;
else
break;
}
for(int i = 1; i <= m; i++)
for(int j = 1; j <= n; j++)
{
if(p[j] == '*')
{
dp[i][j] = dp[i][j-2] || (p[j-1] == '.' || p[j-1] == s[i]) && dp[i-1][j];
}
else if(s[i] == p[j] || p[j] == '.')
{
dp[i][j] = dp[i - 1][j - 1];
}
}
return dp[m][n];
}
};
5.交错字符串(中等)
链接:交错字符串
-
状态表示
有前面的做题经验,我们定义一个二维表,定义状态表示为dp[i] [j]:s1的[0, i]区间和s2的[0, j]区间能否交错组成s3的[0, i + j]区间。 -
状态转移方程
对s1的[0,i]区间和s2的[0,j]区间能否交错组成s3的[0, i + j]区间,我们分情况讨论:
(1)s1[i] == s3[i + j]。这个时候只要s1的[0, i - 1]区间和s2的[0, j]区间可以组成s3的[0,i + j - 1]区间即真,即dp[i] [j] = (s1[i] == s3[i + j] && dp[i - 1] [j])
(2)s2[j] == s3[i + j]。这个时候只要s1的[0, i]区间和s2的[0, j - 1]区间可以组成s3的[0,i + j - 1]区间即真,即dp[i] [j] = (s2[j] == s3[i + j] && dp[i] [j - 1])
以上情况只要一个为真dp[i] [j]就为真。 -
初始化
为了避免越界以及方便初始化,我们引入空串的概念,多开一行一列。
①其中s1和s2都为空串可以组成空串s3,即dp[0][0] = true。
②当s1为空串,s2不为空串(第一列除去[0, 0])的时候可以由s2单独组成s3,前提是相等。即dp[0] [j] = true([1, j]区间s2与s3相等)。
③当s2为空串,s1不为空串(第一行除去[0, 0])的时候可以由s1单独组成s3,前提是相等。即dp[i] [0] = true([1, i]区间s1与s3相等)。 -
填表顺序
填表不明白参考第一题,填表顺序为行从上到下,每一行从左到右。 -
返回值
依据状态表示,返回值为dp[m] [n](m,n分别为s1、s2长度)。
- 代码实现
class Solution
{
public:
bool isInterleave(string s1, string s2, string s3)
{
int m = s1.size(), n = s2.size();
if(m + n != s3.size()) return false; //两者相加比s3长度小,一定没办法组成的
s1 = " " + s1, s2 = " " + s2, s3 = " " + s3; //处理下标映射
//dp[i][j]:s1的[1,i]区间和s2的[1,j]区间能否交错组成s3的[1,i+j]区间
vector<vector<bool>> dp(m + 1, vector<bool>(n + 1));
dp[0][0] = true;
for(int j = 1; j <= n; j++) // 初始化第⼀⾏,即s1为空,s2单独组成s3
{
if(s2[j] == s3[j]) dp[0][j] = true;
else break;
}
for(int i = 1; i <= m; i++) // 初始化第⼀列,即s2为空,s1单独组成s3
{
if(s1[i] == s3[i]) dp[i][0] = true;
else break;
}
for(int i = 1; i <= m; i++)
for(int j = 1; j <= n; j++)
dp[i][j] = (s1[i] == s3[i + j] && dp[i - 1][j])
|| (s2[j] == s3[i + j] && dp[i][j - 1]);
return dp[m][n];
}
};
6.两个字符串的最小ASCII删除和(中等)
链接:两个字符串的最小ASCII删除和
-
状态表示
有前面的做题经验,我们定义一个二维表,定义状态表示为dp[i] [j]:s1的[0, i]区间和s2的[0, j]区间要达到相同的最小删除消耗。 -
状态转移方程
对s1的[0,i]区间和s2的[0,j]区间如何相同,我们分情况讨论:
(1)s1[i] == s2[j]时,只需要让s1的[1, i - 1]和s2[1, j - 1]相同,即dp[i] [j] = dp[i - 1] [j - 1]。
(2)s1[i] != s2[j]时,有两种选择:
①让s1的[1, i - 1]和s2的[1, j]相同,把多余的s1[i]删除,即dp[i] [j] = dp[i - 1] [j] + s1[i]。
②s1的[1, i]和s2的[1, j -1]相同,把多余的s2[j]删除,即dp[i] [j] = dp[i] [j - 1] + s2[j]。
取①②情况的最小值即可,即(2)情况dp[i][j] = min(dp[i] [j - 1] + s2[j], dp[i - 1] [j] + s1[i])。
这里提一下(1)情况的消耗是一定小于等于(2)的消耗,比如我一个短串和一个长串达到相等的消耗了x。现在我在短串后面加一些字符,想达到相等的话消耗一定会大于等于x。 -
初始化
为了避免越界以及方便初始化,我们引入空串的概念,多开一行一列。
①当s1和s2都为空串,消耗为0,即dp[0] [0] = 0。
②当s1为空串,s2不为空串(第一列除去[0, 0])的时候s2必须全部删除一直到为空串。即dp[0] [j] = dp[0] [j - 1] + s2[j] (j = 1; j <= n; j++)。
③当s2为空串,s1不为空串(第一行除去[0, 0])的时候s1必须全部删除一直到为空串。即dp[i] [0] = dp[i - 1] [0] + s1[i] (i = 1; i <= m; i++)。 -
填表顺序
填表不明白参考第一题,填表顺序为行从上到下,每一行从左到右。 -
返回值
依据状态表示,返回值为dp[m] [n](m,n分别为s1、s2长度)。
- 代码实现
class Solution {
public:
int minimumDeleteSum(string s1, string s2) {
int m = s1.size(), n = s2.size();
s1 = " " + s1, s2 = " " + s2; //处理下标映射
//dp[i][j]:s1的[1,i]区间和s2的[1,j]区间要达到相同的最小删除消耗
vector<vector<int>> dp(m + 1, vector<int>(n + 1));
//s1为空串,s2要删除为空串的最小消耗
for(int j = 1; j <= n; j++)
dp[0][j] = dp[0][j - 1] + s2[j];
//s2为空串,s1要删除到空串的最小消耗
for(int i = 1; i <= m; i++)
dp[i][0] = dp[i - 1][0] + s1[i];
for(int i = 1; i <= m; i++)
for(int j = 1; j <= n; j++)
{
if(s1[i] == s2[j])
dp[i][j] = dp[i - 1][j - 1];
else
dp[i][j] = min(dp[i][j - 1] + s2[j], dp[i - 1][j] + s1[i]);
}
return dp[m][n];
}
};
7.最长重复子数组(中等)
链接:最长重复子数组
-
状态表示
这个题不难,但是注意它是子数组而不是子序列,我们用前面的方式定义状态表示是会出错的,比如我定义状态表示为dp[i] [j]:n1的[0, i]区间与n2的[0, j]区间中的公共最长子数组长度。
拿n1 = [3, 1, 1]和n2 = [1, 0, 1]举例,n1的[3, 1]区间和n2的[1, 0]区间公共最长子数组长度为1,当n1[2] == n2[2]的时候,公共最长子数组是没办法算的,你想dp[i - 1][j - 1] + 1是绝对不行的,因为n1[2]和n2[2]不一定能接在这个最长子数组后面,子数组必须是连续的!!!
前面以区间为关注对象,没办法推导状态转移方程,那我们就以n1[i]和n2[j]为子数组结尾进行分析。
我们定义一个二维表,定义状态表示为dp[i] [j]:同时以n1的i位置和n2的j位置结尾的公共最长子数组长度。 -
状态转移方程
对n1[i]和n2[j],我们分情况讨论:
(1)n1[i] == n2[j]时,可以同时接在以n1[i - 1]和n2[j - 1]为结尾的公共最长子数组后面,长度加1,即dp[i] [j] = dp[i - 1] [j - 1] + 1。
(2)n1[i] != n2[j]时,同时以n1[i]和n2[j]为结尾的公共最长子数组不存在,即dp[i] [j] = 0。 -
初始化
为了避免越界,我们多开一行一列,dp数组下标从1开始,多出来的一行一列初始化为0即可。(注意处理与n1和n2数组的下标映射,因为n1和n2数组是从下标0开始的) -
填表顺序
填表顺序为行从上到下,每一行从左到右。 -
返回值
没法直接确定最长子数组的结尾,所以一边dp一边更新最大值。
- 代码实现
class Solution {
public:
int findLength(vector<int>& n1, vector<int>& n2) {
int m = n1.size(), n = n2.size();
//dp[i][j]表示以nums1的i位置和nums2的j位置结尾的公共最长子数组长度
vector<vector<int>> dp(m + 1, vector<int>(n + 1));
int ret = 0;
for(int i = 1; i <= m; i++)
for(int j = 1; j <= n; j++)
{
if(n1[i - 1] == n2[j - 1]) //注意下标映射
dp[i][j] = dp[i - 1][j - 1] + 1;
ret = max(ret, dp[i][j]);
}
return ret;
}
};