力扣76. 最小覆盖子串

给你一个字符串 s 、一个字符串 t 。返回 s 中涵盖 t 所有字符的最小子串。如果 s 中不存在涵盖 t 所有字符的子串，则返回空字符串 "" 。

注意：

对于 t 中重复字符，我们寻找的子字符串中该字符数量必须不少于 t 中该字符数量。
如果 s 中存在这样的子串，我们保证它是唯一的答案。
 

示例 1：

输入：s = "ADOBECODEBANC", t = "ABC"
输出："BANC"
示例 2：

输入：s = "a", t = "a"
输出："a"
示例 3:

输入: s = "a", t = "aa"
输出: ""
解释: t 中两个字符 'a' 均应包含在 s 的子串中，
因此没有符合条件的子字符串，返回空字符串。
 

提示：

1 <= s.length, t.length <= 105
s 和 t 由英文字母组成
 

进阶：你能设计一个在 o(n) 时间内解决此问题的算法吗？

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/minimum-window-substring
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

class Solution {
public:
    string minWindow(string s, string t) {
        unordered_map need,window;
        for(char c:t){
            need[c]++;
        }
        int left=0,right=0,valid=0;
        //记录最小覆盖子串的起始索引和长度
        int start=0,len=INT_MAX;
        while(right

---

滑动窗口算法的代码框架：

/* 滑动窗口算法框架 */
void slidingWindow(string s, string t) {
    unordered_map need, window;
    for (char c : t) need[c]++;
    
    int left = 0, right = 0;
    int valid = 0; 
    while (right < s.size()) {
        // c 是将移入窗口的字符
        char c = s[right];
        // 右移窗口
        right++;
        // 进行窗口内数据的一系列更新
        ...

        /*** debug 输出的位置 ***/
        printf("window: [%d, %d)\n", left, right);
        /********************/
        
        // 判断左侧窗口是否要收缩
        while (window needs shrink) {
            // d 是将移出窗口的字符
            char d = s[left];
            // 左移窗口
            left++;
            // 进行窗口内数据的一系列更新
            ...
        }
    }
}

unordered_map 就是哈希表（字典），它的一个方法 count(key) 相当于 Java 的 containsKey(key) 可以判断键 key 是否存在。

可以使用方括号访问键对应的值 map[key]。需要注意的是，如果该 key 不存在，C++ 会自动创建这个 key，并把 map[key] 赋值为 0。

所以代码中多次出现的 map[key]++ 相当于 Java 的 map.put(key, map.getOrDefault(key, 0) + 1)

初始化 window 和 need 两个哈希表，记录窗口中的字符和需要凑齐的字符：

valid 变量表示窗口中满足 need 条件的字符个数，如果 valid 和 need.size 的大小相同，则说明窗口已满足条件，已经完全覆盖了串 T。

套滑动窗口模板，只需要思考以下四个问题：

1、当移动 right 扩大窗口，即加入字符时，应该更新哪些数据？

2、什么条件下，窗口应该暂停扩大，开始移动 left 缩小窗口？

3、当移动 left 缩小窗口，即移出字符时，应该更新哪些数据？

4、我们要的结果应该在扩大窗口时还是缩小窗口时进行更新？

如果一个字符进入窗口，应该增加 window 计数器；如果一个字符将移出窗口的时候，应该减少 window 计数器；当 valid 满足 need 时应该收缩窗口；应该在收缩窗口的时候更新最终结果。

---

滑动窗口算法的思路是这样：

1、我们在字符串 S 中使用双指针中的左右指针技巧，初始化 left = right = 0，把索引左闭右开区间 [left, right) 称为一个「窗口」。

2、我们先不断地增加 right 指针扩大窗口 [left, right)，直到窗口中的字符串符合要求（包含了 T 中的所有字符）。

3、此时，我们停止增加 right，转而不断增加 left 指针缩小窗口 [left, right)，直到窗口中的字符串不再符合要求（不包含 T 中的所有字符了）。同时，每次增加 left，我们都要更新一轮结果。

4、重复第 2 和第 3 步，直到 right 到达字符串 S 的尽头。

这个思路其实也不难，第 2 步相当于在寻找一个「可行解」，然后第 3 步在优化这个「可行解」，最终找到最优解，也就是最短的覆盖子串。左右指针轮流前进，窗口大小增增减减，窗口不断向右滑动，这就是「滑动窗口」这个名字的来历。

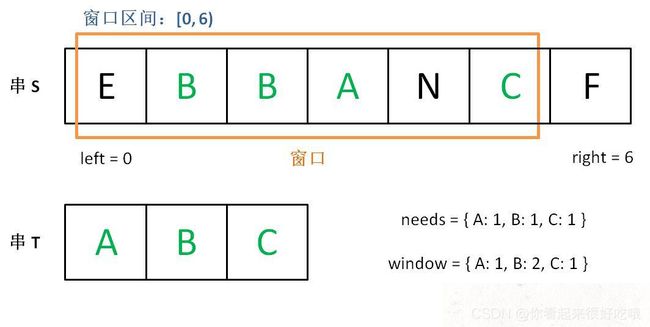
下面画图理解一下，needs 和 window 相当于计数器，分别记录 T 中字符出现次数和「窗口」中的相应字符的出现次数。

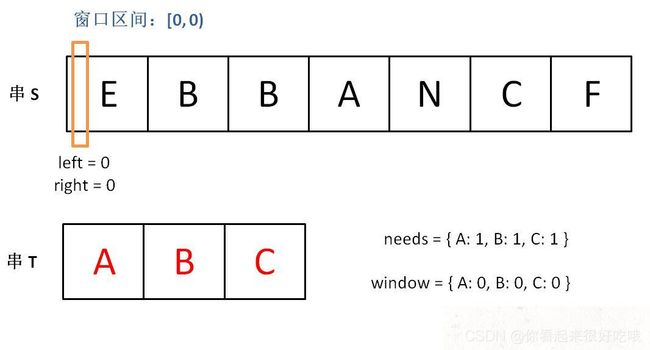
初始状态：

增加 right，直到窗口 [left, right] 包含了 T 中所有字符：

 

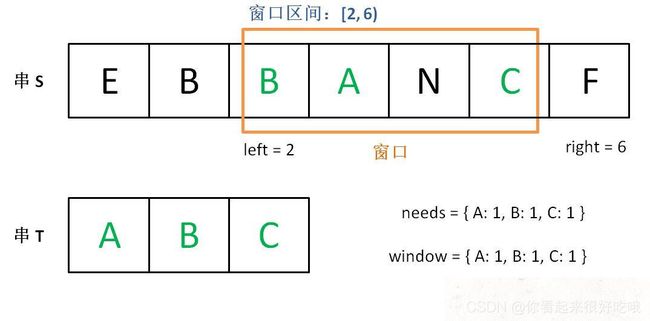
 现在开始增加 left，缩小窗口 [left, right]。

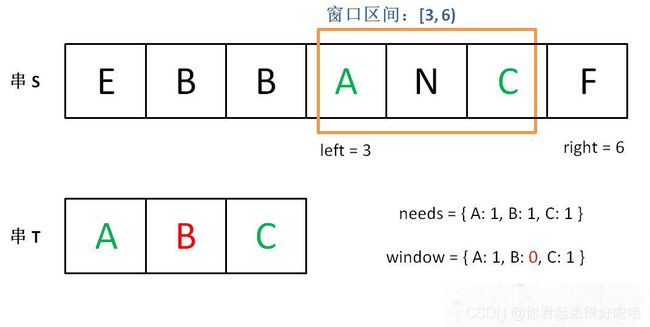
 直到窗口中的字符串不再符合要求，left 不再继续移动。

之后重复上述过程，先移动 right，再移动 left…… 直到 right 指针到达字符串 S 的末端，算法结束。