万字长文:人脸识别综述(学习笔记)
人脸的检测与识别是一个历史悠久的方向,之前没做过相关的工作,所以对人脸检测的相关流程没有很清晰的概念。工作原因,近期对人脸识别的来龙去脉做一个笔记和知识梳理,从上到下的一个pipeline,文章部分内容有引用或摘抄均给出了出处,如有侵权,还望及时与笔者联系进行删除或整改。
作者:Wisley
邮箱:[email protected]
GitHub:个人主页
人脸识别
-
- 一、人脸识别背景
- 二、人脸识别算法
-
- 2.1 人脸检测
- 2.2 人脸关键点定位
-
- 2.2.1 ASM模型
- 2.2.2 AAM 模型
- 2.1.3 CLM模型
- 2.3 人脸对齐
- 2.4 人脸表征
-
- 2.4.1 人脸识别模型的评价指标
-
- 2.4.1.1 TPR和FPR
- 2.4.1.2 TAR 和FAR
- 2.4.1.3 TAR @ FAR=0.001
- 2.4.1.4 ROC 曲线
- 2.4.2 人脸识别中的损失函数
-
- 2.4.2.1 Triplet loss
- 2.4.2.2 Center loss
- 2.4.2.1 ArcFace loss
- 2.5 人脸匹配
- 2.6 小结
- 三、参考文献
一、人脸识别背景
人脸识别作为一种非入侵式的识别验证方式相比其他生物识别技术更受大众的喜爱与接受,随着识别技术的发展与进步,人脸识别技术已广泛部署在多种场景下如监控系统、安防系统、工业生产、家庭监护等,方便人们生活的各方各面。人脸识别的其它常见应用还包括访问控制、欺诈检测、身份认证和社交媒体等。
人脸识别主要可以分为以下三种场景模式,分别为1:1,1:N,N:N。
- 1:1 问题
银行柜台、海关、手机解锁、酒店入住、网吧认证,会查身份证跟你是不是同一个人。这个应用的主要特点是,在大多数场景下都需要你先提供一个证件,然后跟自己的人脸做比对。简单来说,这个问题就是给定两张图片,判断是否是一个人,相当于做一个二分类 - 1:N问题
在图书馆,公司等重要场所,我们往往需要对人脸进行检索没判断这个人有没有出现在人脸库中,相当于一张图片,要与库中的每张人脸进行比对,判断是否一致,直到所有匹配的回答都是否时,才意味这个人不在我们的人脸库中,而不予以通过。实际使用时一般是静态的搜索,返回TOP K个的相似人脸,这个和推荐系统领域的粗排,精排的目的相似。 - N:N问题
在安防或者其他应用场景则有更难的任务,我们的城市有数不清的摄像头,每天都会产生大量的抓拍图片,同时对比库也是非常大大,这就是N张图片进行N次搜索的问题。比如我们100个摄像头,每个摄像头一天抓拍了1万个人,而我们的底库有10万,总共搜索量精需要100x1w的搜索量。我们有10个嫌疑人,现在我们的算法,报警量100次,最后抓到9个人,感觉还是可以的,10个人抓到9个,召回率有90%,而且误报率也非常低。但是实际却不行,因为出警率有100次,却抓到9个嫌疑人,只有9%的准确率,实际上我们希望每次出警都能准确定位出嫌疑人。
人脸识别不同于简单的图片分类任务,它是个开集任务,即对于测试集的分类目标,不存在于训练集中。这也非常好理解,因为我们拿到用于训练的人脸图片,与现场进行抓拍的人脸图片肯定是不一致的,同时也无法做到将全世界所有人的人脸都收集起来训练。在其次就是场景、设备、光线、妆容、表情、年龄等各方面因素,都会使得同一个人的照片出现天差地别的变化,这需要模型有较好的鲁棒性,能够从人脸中提取稳健的特定特征。
二、人脸识别算法
人脸识别的基本流程:
- 人脸检测
- 人脸关键点定位
- 人脸对齐
- 人脸表征
- 人脸匹配
2.1 人脸检测
人脸检测是通过模型或算法来寻找图片中人脸的位置,输出人脸边界框的坐标,以将检测到的人脸输送到后续模型中。现有的人脸检测模型有很多,与目标检测的一类模型如RCNN、YOLO、Retina等框架通用,同时在人脸检测时,模型还可以输出关键点坐标以及相关属性等信息。

2.2 人脸关键点定位
人脸特征点检测是指定位脸部预定义的关键点,比如眼睛、鼻子、嘴巴等。定位的目的是在人脸检测的基础上,进一步确定脸部特征点(眼睛、眉毛、鼻子、嘴巴、脸部外轮廓)的位置。传统的定位算法的基本思路是:人脸的纹理特征和各个特征点之间的位置约束相结合。
人脸特征点检测的方法可以分成:
- 基于参数化模型的方法:ASM、AAM、CLM等
- 基于回归的方法:ESR、SDM、RCPR、LBP等
- 基于神经网络的方法:包括CNN/RNN/FCN等
这里简单介绍一些传统方法,感兴趣的小伙伴可以自行细查阅相关资料,这里不做过多详细的说明。
2.2.1 ASM模型
参考
ASM是一种基于点分布模型(Point Distribution Model, PDM)的算法,起源于snake模型(作为动态边缘分割的snake模型),该方法用一条由n个控制点组成的连续闭合曲线作为snake模型,再用一个能量函数作为匹配度的评价函数,首先将模型设定在目标对象预估位置的周围,再通过不断迭代使能量函数最小化,当内外能量达到平衡时即得到目标对象的边界与特征。
原始Snakes模型由一组控制点:v(s)=[x(s), y(s)] s∈[0, 1] 组成,这些点首尾以直线相连构成轮廓线。其中x(s)和y(s)分别表示每个控制点在图像中的横纵坐标位置。 s 是以傅立叶变换形式描述边界的自变量。snake的大致思路是先给定一个坐标曲线,然后通过最小化能量函数来得到最优解,这个最优解会让曲线趋近于平滑且靠近目标边缘。能量函数如公式(1)所示。
E total = ∫ s ( α ∣ ∂ ∂ s v ⃗ ∣ 2 + β ∣ ∂ 2 ∂ s 2 v ⃗ ∣ 2 + E e x t ( v ⃗ ( s ) ) ) d s ( 1 ) E_{\text {total }}=\int_{s}\left(\alpha\left|\frac{\partial}{\partial s} \vec{v}\right|^{2}+\beta\left|\frac{\partial^{2}}{\partial s^{2}} \vec{v}\right|^{2}+E_{e x t}(\vec{v}(s))\right) ds \qquad(1) Etotal =∫s(α∣∣∣∣∂s∂v∣∣∣∣2+β∣∣∣∣∂s2∂2v∣∣∣∣2+Eext(v(s)))ds(1)
其中第1项称为弹性能量是v的一阶导数的模,第2项称为弯曲能量,是v的二阶导数的模,弹性能量和弯曲能量合称内部能量(内部力),用于控制轮廓线的弹性形变,起到保持轮廓连续性和平滑性的作用。第3项是外部能量(外部力),表示变形曲线与图像局部特征吻合的情况。一般只取控制点或连线所在位置的图像局部特征例如梯度,如公式(2)所示。当轮廓C靠近目标图像边缘,那么C的灰度的梯度将会增大,那么上式的能量最小。
E e x t ( v ⃗ ( s ) ) = P ( v ⃗ ( s ) ) = − ∣ ∇ I ( v ) ∣ 2 ( 2 ) E_{e x t}(\vec{v}(s))=P(\vec{v}(s))=-|\nabla I(v)|^{2} \qquad (2) Eext(v(s))=P(v(s))=−∣∇I(v)∣2(2)
在能量函数极小化过程中,弹性能量迅速把轮廓线压缩成一个光滑的圆,弯曲能量驱使轮廓线成为光滑曲线或直线,而图像力则使轮廓线向图像的高梯度位置靠拢。基本Snakes模型就是在这3个力的联合作用下工作的。
ASM模型在实际训练中包含训练和搜索两个部分(详细参考)。
- 1、建立形状模型:
- 1.1 收集包含人脸的训练集
- 1.2 手动标记K个关键点
- 1.3 构建形状向量(坐标)
- 1.4 形状归一化(通过平移,旋转,缩放,在不改变点分布模型的基础上对齐到同一个点分布模型,采用Procrustes方法)
- 1.5 对齐后的形状向量进行PCA处理
- 2、构建特征点的局部特征
- 如通过计算局部灰度值的梯度得到纹理特征,通过迭代的方式跟新特征点
- 3、搜索
- 对平均形状通过平移,缩放,旋转得到初始模型,通过搜索得到最终形状。
- 计算相似度,相似度为局部特征的马氏距离,新的目标特征点为前后特征点连线方向上,以其为中心两边各选择l个像素点计算局部特征,通过计算这些子局部特征与当前特征点之间的马氏距离最小的子局部特征中心,作为当前特征点的新位置
参考:1、2
2.2.2 AAM 模型
参考文献:Active Appearance Models、Active Shape Models
前面说到,ASM是基于统计形状模型的基础上进行的,而AAM则是在ASM的基础上,进一步对纹理(将人脸图像变形到平均形状而得到的形状无关图像g)进行统计建模,并将形状和纹理两个统计模型进一步融合为表观模型。
AAM模型相对于ASM模型的主要改进为:使用两个统计模型融合来取代 ASM的灰度模型。主要对特征点的特征描述子进行了改进,增加了描述子的复杂度和鲁棒性。
2.1.3 CLM模型
引用:【机器学习理论与实战(十六)概率图模型04】
CLM(Constrained local model)顾名思义就是有约束的局部模型,ASM、AAM都属于有约束的局部模型,它通过初始化平均脸的位置,然后让每个平均脸上的特征点在其邻域位置上进行搜索匹配来完成人脸点检测。整个过程分两个阶段:模型构建阶段和点拟合阶段。模型构建阶段又可以细分两个不同模型的构建:形状模型构建和Patch模型构建,如(图一)所示。形状模型构建就是对人脸模型形状进行建模,说白了就是一个ASM的点分布函数(PDM),它描述了形状变化遵循的准则。而Patch模型则是对每个特征点周围邻域进行建模,也就说建立一个特征点匹配准则,怎么判断特征点是最佳匹配。
相关论文可以参考这篇文章的工作:Deformable Model Fitting by Regularized Landmark Mean-Shift
2.3 人脸对齐
人脸对齐是将人脸模型与图像进行匹配并提取人脸像素的语义的一种方法,它是人脸图片送入模型提取特征前的预处理工作,主要目的是将形态各异、不规则的人脸图片,校正到统一的模板,方便模型提取特征,从而提高模型精度。它使用一组位于人脸图片中标准位置的固定坐标作为参考点,通过仿射变换将原始的人脸图片变换到标准模板上。这个过程需要通过检测器得到原始人脸图片上的关键点坐标,再与参考点使用最小二乘法计算仿射变换的参数矩阵。
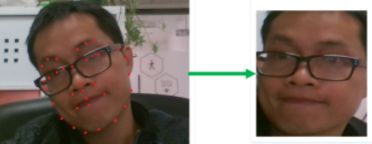
人脸对齐也是一项历史悠久的工作,现如今已有非常多的方法,如传统的约束模型,概率模型,到后来的回归模型、树模型,到现在层出不穷的深度模型、图卷积、点云等技术。一般来说,关键点的检测也容易受光线、角度、纹理、遮挡等因素的影响。从关键点定位到对齐,主要方法的类别还分为:2D方法,3D方法,稀疏方法和密集方法等。另外如于深度学习方法可以很好的实现对多任务的处理,因此有很多新的算法可以同时完成人脸框检测以及对2D关键点和3D关键点的获取,进而可进一步支持后续的多任务分析。
人脸对齐也面临很多挑战,大多数对齐算法都是为小到中等姿态(45度以下)的脸设计的,缺乏在高达90度的大姿态中对齐脸的能力;同时常用的基于参考坐标的算法,都是假设再所有人脸中均可见的(无遮挡),这是不合理的。同时稠密人脸、三维人脸、大姿态人脸等场景下也面临极大的挑战。Xiangyu等人的工作Face Alignment Across Large Poses: A 3D Solution则提出了三维密集人脸对齐(3D Dense Face alignment, 3DDFA)框架,来解决这些问题,该框架通过卷积神经网络(CNN)将稠密的三维人脸模型拟合到图像上。同时他们还提出了一种在剖面视图中合成大规模训练样本的方法来解决数据标记等问题。
\quad
2.4 人脸表征
人脸表征是将人脸图像转化为具有代表性的特征向量,用于后续的人脸匹配等工作。一个好的表征向量应该是同一个主体的所有人脸图片都能映射到相类似的向量上,不同主体之间的特征向量具有一定的差距(如较大的欧氏距离或者余弦距离等)。人脸表征在整个人脸识别当中算是最主要的一步,也是我们主要学习和介绍的重点。
基于CNN的人脸识别方法是目前领域内最常见的一类方法,其主要优点是使用大量数据训练,从而学习到稳健的人脸表征,它不同于以往的方法,不需要手工设计人脸特征,并在数据集规模扩大的同时能适用于更加复杂的人脸场景。影响基于深度学习的人脸识别算法主要有三个方面:
- 1、数据规模和质量。一定规模的训练数据能提高模型的鲁棒性(如更多的主体数量、每个主体下形态各异的图片数量等),学习到更好的表征向量。而数据集的质量包括清晰度、角度、光照等。
- 2、网络结构。不同的网络模型结构也影响模型的识别能力,典型的网络结构有VGG、Resnet等,均可借鉴图片分类中的一些 网络结构
- 3、优化和训练方法。人脸识别是个开集问题,不同于简单的图片分类任务,合理设计优化目标是提高模型精度的关键。常用的方法有优化配对人脸或者人脸三元组之间的距离度量、选择不同损失函数如:Center loss、Arcface等。
2.4.1 人脸识别模型的评价指标
在介绍人脸识别模型前,我们先来学习下人脸识别中常用的衡量指标。在人脸识别中常用到的指标是TAR(True Accept Rate)和FAR(False Accept Rate),他们与TPR(True Positive Rate)和FPR(False Positive Rate)有略微的差异。
2.4.1.1 TPR和FPR
首先来看我们熟悉的TPR(True Positive Rate)和FPR(False Positive Rate),TPR(True Positive Rate)和FPR(False Positive Rate)是二分类算法常用的评价指标,分别是真正例率和假正例率。他们都是基于混淆矩阵的度量标准。混淆矩阵如下所示:
| n=192 | Predict 0 | Predict 1 |
|---|---|---|
| Actual 0 | 118 | 12 |
| Actual 1 | 14 | 15 |
- 真正类 (True Positive,TP):被分类器预测为正的正样本 (预测正确)
- 真负类 (True Negative,TN):被分类器预测为负的负样本 (预测正确)
- 假正类 (False Positive,Fp):被分类器预测为正的负样本 (预测错误)
- 假负类 (False Positive,Fp):被分类器预测为负的正样本 (预测错误)
那么TPR与FPR的计算可以根据混淆矩阵进行计算,如下:
TPR(True Positive Rate)真正率,也叫召回率或灵敏率:模型正确识别的正样本在实际正样本中的比例:
T P R = T P T P + F N \mathrm{TPR}=\frac{\mathrm{TP}}{\mathrm{TP}+\mathrm{FN}} TPR=TP+FNTP
FPR (True Positive Rate)假正率, 模型错误识别为正样本在实际负样本中的比例:
F P R = F P T N + F P \mathrm{FPR}=\frac{\mathrm{FP}}{\mathrm{TN}+\mathrm{FP}} FPR=TN+FPFP
混淆矩阵还能度量其他一些指标,如准确率,AUC,ROC等。
2.4.1.2 TAR 和FAR
人脸识别中的常用的指标TAR和FAR。TAR(True Accept Rate)表示正确接受的比例,FAR(False Accept Rate)表示错误接受的比例。所谓的接受就是在进行人脸验证的过程中,两张图像被认为是同一个人。
FAR(False Accept Rate) 的计算方式如下:
F R R = 负对分数 > T 负对总数 \mathrm{FRR}=\frac{\text { 负对分数 }>\mathrm{T}}{\text { 负对总数 }} FRR= 负对总数 负对分数 >T
做人脸验证的时候,我们将两张图片Eembedding成两个高维的特征向量,然后计算两个特征向量的相似度或者距离(一般为余弦距离)。公式中分数指的就是两两图片的相似度得分。
在建立比对数据时,我们把同一个人的两张图片称为正对(同人),不同人的两张图片称为负对(非同人)。在两两相似度计算后,我们希望同一个人的图像相似度比较高,不同人的相似度比较低。我们会给定一个相似度阈值T,比如0.6, 如果两张图像的相似度大于T我们就认为两张图片是一个人的,如果小于T我们就认为两证图像是不同人的。但是无论将T设置成什么样值都会有一定得错误率,就是FAR,因为我们提取的图像的特征向量总是不够好,并不总能 满足:同一个人的图像相似度比较高,不同人的相似度比较低。偶尔也会出现不同人的图像的相似度大于给定的阈值T,这样我们就会犯接受的错误。FAR就是我们比较不同人的图像时,把负对(两张不同的人脸)图像对当成同一个人图像占所有负对的比例。我们希望FAR越小越好。
TAR(True Accept Rate) 表示正确接受的比例,计算方式如下:
F R R = 正对分数 < T 正对总数 \mathrm{FRR}=\frac{\text { 正对分数 }<\mathrm{T}}{\text { 正对总数 }} FRR= 正对总数 正对分数 <T
TAR 表示了在正对中,被预测为正的样本数占所有正对的比例。同样,对于给定阈值T,正对的预测分数(同人分数)大于T,表示了模型正确预测的数量。
2.4.1.3 TAR @ FAR=0.001
在阅读人脸相关论文时,经常会看到 TAR @ FAR=0.001 这样的算法性能报告,意思就是在FAR为0.001的情况下,TAR是多少。一般来说,当给定FAR时,根据公式,我们能够计算出阈值T,再根据阈值T,我们就能计算出对应的TAR为多少。TAR与FAR是一对相互对立的指标,一般来说,在同一组模型预测结果中,TAR减少,FAR就会增加,反之亦然。所以在报告TAR时,只有说明FAR为多少时才有意义。
一般在评价算法的性能时,我们会统计在不同数量级的FAR下,TAR的分数,构成ROC曲线。相同FRR下,TAR的值越大,则模型的性能越好。
2.4.1.4 ROC 曲线
进一步,在人脸识别中,对模型进行评估时,我们还会画出ROC曲线,来直观地对比模型的性能,ROC 曲线为TPR-FPR的相关曲线,横坐标为假正率,纵坐标为正正率,通过设定一系列的阈值,我们就能得到不同阈值下的横纵坐标,从而画出ROC曲线图。如下图所示:
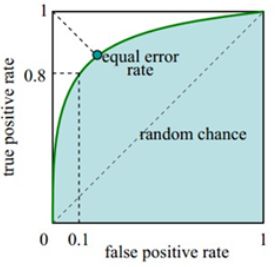
该曲线一定经过(0,0)点与(1,1)点,曲线与坐标轴所包含的面积(绿色区域)越大,表示模型的性能越好。理想的最佳状态是无论FPR为多少,TPR都非常高(接近1),此时曲线与坐标轴围城的面积最大。
2.4.2 人脸识别中的损失函数
对于损失函数的研究是近年来在人脸识别领域活跃的热点方向。朴素的做法是参考像图片分类任务使用sofrmax损失训练,把每个主体当作一种类别,但是使用这种损失函数无法很好地泛化测试集中未出现在训练集中的主体上。softmax损失能将指导模型学习主体间的差异,增加类间距离,但是对于类内距离并没有约束,并且对于新出现的类别无法分配足够的决策边界。一种解决方法是使用度量学习来进行训练,将人脸图片进行配对得到对比损失,以此监督模型有向训练。
2.4.2.1 Triplet loss
最常见的度量学习方法是三元组损失函数(Triplet loss),该损失函数的目标是以一定的余量(间隔),将正对与负对的距离分开。数学表示如下公式(3):
∥ f ( x a ) − f ( x p ) ∥ 2 2 + α < ∥ f ( x a ) − f ( x n ) ∥ 2 2 ( 3 ) \left\|f\left(\boldsymbol{x}_{a}\right)-f\left(\boldsymbol{x}_{p}\right)\right\|_{2}^{2}+\alpha<\left\|f\left(\boldsymbol{x}_{a}\right)-f\left(\boldsymbol{x}_{n}\right)\right\|_{2}^{2}\qquad(3) ∥f(xa)−f(xp)∥22+α<∥f(xa)−f(xn)∥22(3)
其中 x a x_a xa 是锚图像, x p x_p xp 是同一主体的图像, x n x_n xn 是另一个不同主体的图像, f f f 是模型学习到的映射关系, α α α是 施加在正例对和负例对距离之间的余量。该表述所表达的思想非常直观,尽可能让正样本距离类主体的距离小于负样本距离类主体的距离。在实际的训练过程,使用三元组损失训练的 CNN 的收敛速度比使用 softmax 的慢,这是因为需要大量三元组(或对比损失中的配对)才能覆盖整个训练集,然而穷举整个训练集的配对样本是比较困难的。有学者提出可以通过在训练阶段赛选难例样本(即违反余量条件的三元组)来缓解 ,常见的做法是在第一个训练阶段使用 softmax 损失训练,在第二个训练阶段使用三元组损失来对一些难例进行微调学习。还有研究者进一步提出了三元组的一些变体,如使用点积作为相似度度量等来进一步优化三元组的训练过程。
2.4.2.2 Center loss
相比于对比损失和三元组损失,中心损失(centre loss)相对更高效且更容易实现,它不需要在训练过程中构建配对或三元组。中心损失的目标是最小化样本特征与它们对应类别的中心之间的距离。通过使用 softmax 损失和中心损失进行联合训练,能够有效增大类间差异(softmax 损失)和降低类内个体差异(中心损失)。如公式(4)所示,其中 L C \mathcal{L}_{C} LC是中心损失,计算的是样本特征向量距离中心的欧式距离。
L = L S + λ L C = − ∑ i = 1 m log e W y i T x i + b y i ∑ j = 1 n e W j T x i + b j + λ 2 ∑ i = 1 m ∥ x i − c y i ∥ 2 2 ( 4 ) \begin{aligned} \mathcal{L} &=\mathcal{L}_{S}+\lambda \mathcal{L}_{C} \\ &=-\sum_{i=1}^{m} \log \frac{e^{W_{y_{i}}^{T} x_{i}+b_{y_{i}}}}{\sum_{j=1}^{n} e^{W_{j}^{T} x_{i}+b_{j}}}+\frac{\lambda}{2} \sum_{i=1}^{m}\left\|\boldsymbol{x}_{i}-\boldsymbol{c}_{y_{i}}\right\|_{2}^{2} \qquad(4) \end{aligned} L=LS+λLC=−i=1∑mlog∑j=1neWjTxi+bjeWyiTxi+byi+2λi=1∑m∥xi−cyi∥22(4)
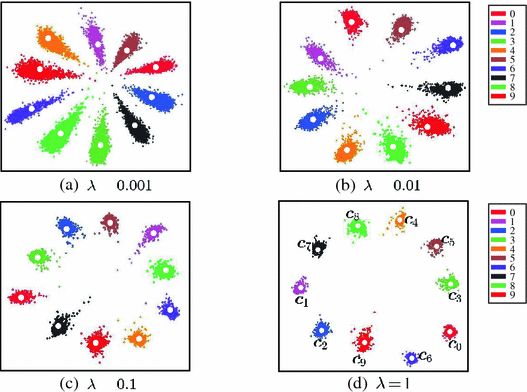
下图是在MINIST数据集上,不同 λ \lambda λ下的训练结果可视化:
2.4.2.1 ArcFace loss
文章链接
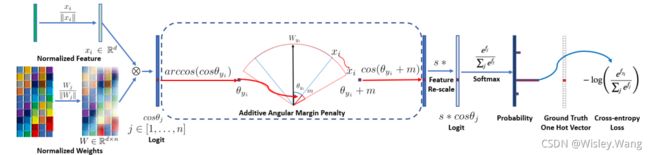
ArcFace是在SphereFace基础上改进了特征向量归一化和加性角度的间隔,提高了类间可分性同时加强类内紧度和类间差异。在ArchFace中是直接在角度空间(angular space)中最大化分类界限,相比CosineFace则是在余弦空间中最大化分类界限。传统的softmax loss如公式(5)所示,其中 W ∈ R d × n W\in\mathbb{R}^{d\times n} W∈Rd×n是训练阶段输出层(也可以叫FC 全连接层)进行类别映射的参数矩阵,其中d是特征维度,n是映射的类别数量。
L = − ∑ i = 1 m log e W y i T x i + b y i ∑ j = 1 n e W j T x i + b j ( 5 ) \mathcal{L}=-\sum_{i=1}^{m} \log \frac{e^{W_{y_{i}}^{T} x_{i}+b_{y_{i}}}}{\sum_{j=1}^{n} e^{W_{j}^{T} x_{i}+b_{j}}} \qquad(5) L=−i=1∑mlog∑j=1neWjTxi+bjeWyiTxi+byi(5)
从公式(5)中可知,直接让偏置项b置0并不影响网络的训练结果。进一步正则化向量 W j W_j Wj与 x i x_i xi,使其 ∥ w j ∥ = 1 \|w_j\|=1 ∥wj∥=1, ∥ x j ∥ = 1 \|x_j\|=1 ∥xj∥=1,并添加一个固定的尺度因子S。则两个向量的点积可表示成 W j T x i = ∥ W j ∥ ∥ x i ∥ cos θ j = cos θ j W_{j}^{T} x_{i}=\left\|W_{j}\right\|\left\|x_{i}\right\| \cos \theta_{j}= \cos \theta_{j} WjTxi=∥Wj∥∥xi∥cosθj=cosθj
这样通过特征和权重的正则化使预测仅取决于特征和权重之间的角度,所学的嵌入特征分布在半径为S的超球体上。
前文提到,仅仅是softmax loss 无法很好地监督模型优化内类距离,为了使得类内样本尽可能靠近我们的类中心,缩小类间差距,我们让 x i x_i xi和 W y j W_{yj} Wyj之间的 θ θ θ加上角度间隔m,以加法的方式惩罚深度特征与其相应权重之间的角度,从而同时增强了类内紧度和类间差异。因此Arcface loss如公式(6)所示:
L = − 1 N ∑ i = 1 N log e s ( cos ( θ y i + m ) ) e s ( cos ( θ y i + m ) ) + ∑ j = 1 , j ≠ y i n e s cos θ j ( 6 ) \mathcal{L}=-\frac{1}{N} \sum_{i=1}^{N} \log \frac{e^{s\left(\cos \left(\theta_{y_{i}}+m\right)\right)}}{e^{s\left(\cos \left(\theta_{y_{i}}+m\right)\right)}+\sum_{j=1, j \neq y_{i}}^{n} e^{s \cos \theta_{j}}} \qquad(6) L=−N1i=1∑Nloges(cos(θyi+m))+∑j=1,j=yinescosθjes(cos(θyi+m))(6)
作者在文中经常与SphereFace和CosineFace进行对比,因此这里我们也分别给出这两个损失函数的公式,如公式(7)和公式(8).
L = − 1 m ∑ i = 1 m log e ∥ x i ∥ cos ( m θ y i ) e ∥ x i ∥ cos ( m θ y i ) + ∑ j = 1 , j ≠ y i n e ∥ x i ∥ cos θ j ( 7 ) \mathcal{L}=-\frac{1}{m} \sum_{i=1}^{m} \log \frac{e^{\left\|x_{i}\right\| \cos \left(m \theta_{y_{i}}\right)}}{e^{\left\|x_{i}\right\| \cos \left(m \theta_{y_{i}}\right)}+\sum_{j=1, j \neq y_{i}}^{n} e\left\|x_{i}\right\| \cos \theta_{j}} \qquad(7) L=−m1i=1∑mloge∥xi∥cos(mθyi)+∑j=1,j=yine∥xi∥cosθje∥xi∥cos(mθyi)(7)
L = − 1 m ∑ i = 1 m log e s ( cos ( θ y i ) − m ) e s ( cos ( θ y i ) − m ) + ∑ j = 1 , j ≠ y i n e s cos θ j ( 8 ) \mathcal{L}=-\frac{1}{m} \sum_{i=1}^{m} \log \frac{e^{s\left(\cos \left(\theta_{y_{i}}\right)-m\right)}}{e^{s\left(\cos \left(\theta_{y_{i}}\right)-m\right)}+\sum_{j=1, j \neq y_{i}}^{n} e^{s \cos \theta_{j}}} \qquad (8) L=−m1i=1∑mloges(cos(θyi)−m)+∑j=1,j=yinescosθjes(cos(θyi)−m)(8)
从上述公式中可以看到,SphereFace是在角度空间乘了惩罚因子m,而CosinFace是在余弦空间减去惩罚因子m。
接下来让我们看看几个损失函数的分类边界(decision boundary),决策边界即是样本输出的logits在两个类别上的值相等,由于分母是一样的,分子都是以e为底,所以只要让两个指数部分相等即可,很容易理解和计算。下表表示的是几种损失的决策边界,图来至:picture。
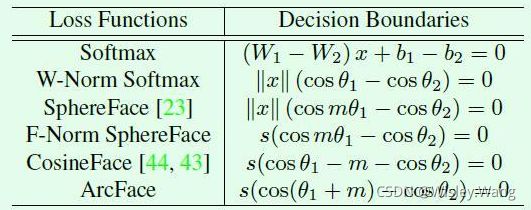
进一步,根据决策边界的公式,以 θ \theta θ为坐标轴,便能画出各损失函数的边界图,如下图所示:
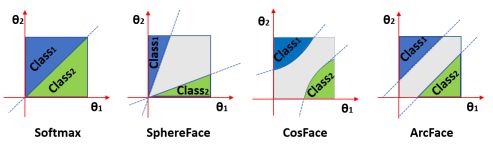
值得一提的是,ArchFace中是直接在角度空间(angular space,横纵坐标是角度θ1和θ2)中最大化分类界限,而CosineFace中是cosθ1和cosθ2是以余弦空间中划分,上图是统一在角度空间画出的。
下图中点表示样本,线表示每个身份的中心方向。在特征归一化的基础上,将人脸所有特征推入固定半径的圆弧空间。当添加角度惩罚后,最接近的类之间的分界线差距变得明显。
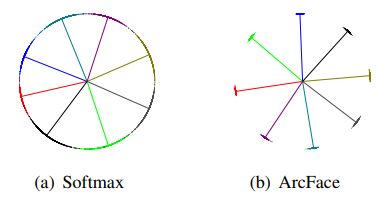
2.5 人脸匹配
人脸识别过程的最后一步就是人脸特征匹配,主要分为两种类型,一种是通过特征算子从图片中提取的特征进行比对;另外一种是现在使用广泛的对特征向量计算相似度,并设定一系列的阈值和策略进行比对归档。
深度学习的广泛应用,使得不需要在手工设计匹配特征,所以如今的匹配大多数是在特征向量上进行的,采用计算余弦相似度来衡量样本间的距离,常用的距离有欧氏距离、 曼哈顿距离 、马氏距离 、信息熵等。当然评价指标也有很多,如本文2.4.1节提到的。在实际的业务场景中,也会根据实际情况制定不同的归档策略和清洗工作,这部分大多是采用机器学习和启发式的方法进行的,最终的策略好坏比较难评估,是以实际的使用体验和落地结果为导向的,这里就不过多介绍了。
2.6 小结
人脸识别领域这些年的发展,已经相当成熟并有很多成功落地的案列,但是复杂多变的环境在一些特定场景下也对算法提出了特殊的要求,如种族歧视、性别歧视、人脸遮挡、密集人脸等问题。这些都有待进一步研究和优化,另外工业界也不同于学术界,讲究准确率的同时还必须做到轻量化与高效性,因此在模型压缩、并行计算上又有很多优化算法和方法需要去具体落地和实现,这些工程问题也非常考验一个算法工程师的能力!! (我们还有很多需要学习的地方! )
这里强烈推荐一个人脸识别开源的项目Insitght Face,里面设计到多个方面的算法代码,能学习到不少东西,且包含mxnet、pytorch、paddle等主流的深度学习框架实现!!
三、参考文献
[1]An Introduction to Active Shape Models. Constrained Local Model for FaceAlignment. Xiaoguang Yan(2011).
[2] A Discriminative Feature Learning Approach for Deep Face Recognition
[3] ArcFace: Additive Angular Margin Loss for Deep Face Recognition
[4] 3DDFA: Face Alignment Across Large Poses- A 3D Solution