生信教程：使用全基因组SNP数据进行ABBA-BABA分析

动动发财的小手，点个赞吧！

简介

ABBA BABA 统计（也称为“D 统计”）为偏离严格的分叉进化历史提供了简单而有力的测试。因此，它们经常用于使用基因组规模的 SNP 数据（例如来自全基因组测序或 RADseq）来测试基因渗入。

在本次实践^[1]中，我们将结合使用可用软件和一些用 R 从头编写的代码来执行 ABBA BABA 分析。我们将分析来自几个 Heliconius 蝴蝶种群的基因组数据。

流程

从多个个体的基因型数据开始，我们首先推断每个 SNP 的等位基因频率。然后，我们计算 D 统计量，然后使用block jackknife来测试与 D=0 的零期望的显着偏差。最后我们估计f“混合比例”。

数据集

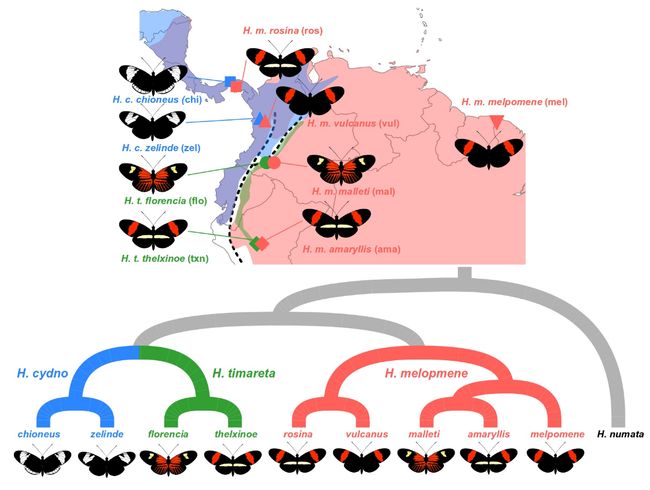
我们将研究三个物种的多个种族：Heliconius melpomene、Heliconius timareta 和 Heliconius cydno。这些物种的分布范围部分重叠，人们认为它们在同源地区发生杂交。我们的样本集包括来自巴拿马和哥伦比亚安第斯山脉西坡的两对同域种群 H. melpomene 和 H. cydno。在哥伦比亚和秘鲁的安第斯山脉东坡，还有两对同域种群：H. melpomene 和 H. timareta。最后，有两个来自外群物种 Heliconius numata 的样本，这是进行 ABBA BABA 分析所必需的。

所有样本均使用深度全基因组测序进行测序，并使用标准流程为每个个体的基因组中每个位点获取基因型。数据经过过滤，「仅保留双等位基因单核苷酸多态性」 (SNP)，并且这些数据已进一步细化，以减小本教程的文件大小。

假设

我们假设同域物种之间的杂交将导致 H. cydno 和来自西方的 H. melpomene 同域种族之间以及 H. timareta 和来自东部的 H. melpomene 相应的同域种族之间共享遗传变异。安第斯山脉。还有来自法属圭亚那的 H. melpomene 的另一个种族，它是 H. timareta 和 H. cydno 的异源性，它应该没有经历过与这两个物种最近的遗传交换，因此可以作为对照。

除了测试基因渗入的存在之外，我们还将测试基因组的某些部分比其他部分经历更多基因渗入的假设。具体来说，我们知道 Z 性染色体上至少有一个位点会导致这些物种之间的杂交雌性不育，这表明一个物种的常染色体与另一个物种的 Z 染色体之间不相容。因此，与常染色体相比，我们可能预期 Z 染色体上的渐渗减少。

全基因组基因渗入测试

在最简单的表述中，ABBA BABA 测试依赖于基因组中与 ABBA 和 BABA 基因型模式相匹配的位点计数。也就是说，给定三个内群体和一个具有关系 (((P1,P2),P3),O) 的外群体，并给定代表每个群体的单个基因组序列（即 H1、H2 和 H3），ABBA 位点是其中 H2 和 H3 共享衍生等位基因（“B”），而 H1 具有祖先状态（“A”），如外群样本所定义。同样，BABA 代表 H1 和 H3 共享衍生等位基因的位点。

忽略重复突变，只有当基因组的某些部分具有不遵循“物种树”的谱系，而是将 H2 与 H3 或 H1 与 H3 分组时，才能产生两种 SNP 模式。如果种群最近才分裂，由于谱系排序的变化，预计基因组的某些部分会出现这种“不一致”的谱系。在没有偏离严格分叉拓扑的情况下，我们预计基因组中大致相同比例的基因组会显示两个不一致的谱系 (((H2,H3),H1),O) 和 (((H1,H3),H2) ，O）。因此，通过计算整个基因组（或其中很大一部分）的 ABBA 和 BABA SNP，我们可以估算出两个不一致的谱系所代表的基因组比例，这意味着我们预计 ABBA 和 BABA SNP 的比例为 1:1。例如，种群 P3 和 P2 之间的基因流动可能会导致偏差，尽管它也可能表明其他打破我们假设的现象，例如祖先种群结构或可变替代率。

为了量化与预期比率的偏差，我们计算 D，它是整个基因组中 ABBA 和 BABA 模式总和的差除以它们的总和：

D = [sum(ABBA) - sum(BABA)] / [sum(ABBA) + sum(BABA)]

因此，D 的范围为 -1 到 1，并且在原假设下应等于 0。 D>1表示ABBA过量，D<1表示BABA过量。

如果我们从每个群体中有多个样本，那么计算 ABBA 和 BABA 位点就不那么简单了。一种选择是仅考虑来自同一群体的所有样本共享相同等位基因的位点，但这会丢弃大量有用数据。更好的选择是使用每个位点的等位基因频率来量化谱系偏向 ABBA 或 BABA 模式的程度。这实际上相当于使用每个位点的所有可能的四个单倍体基因组组来计算 ABBA 和 BABA SNP。因此，ABBA 和 BABA 不再是二元状态，而是 0 到 1 之间的数字，代表与每个谱系匹配的等位基因组合的频率。它们是根据每个群体中派生等位基因 (p) 和祖先等位基因 (1-p) 的频率计算的，如下所示：

ABBA = (1-p1) x p2 x p3 x 1-pO

BABA = p1 x (1-p2) x p3 x 1-pO

实战

准备

打开终端窗口并导航到将运行练习并存储所有输入和输出数据文件的文件夹。现在创建一个名为“data”的子目录并下载本教程所需的数据文件

mkdir data

cd data

wget https://github.com/simonhmartin/tutorials/raw/master/ABBA_BABA_whole_genome/data/hel92.DP8MP4BIMAC2HET75dist250.geno.gz

wget https://github.com/simonhmartin/tutorials/raw/master/ABBA_BABA_whole_genome/data/hel92.pop.txt

cd ..

接下来，在 GitHub 上下载本教程所需的 python 脚本集合

wget https://github.com/simonhmartin/genomics_general/archive/master.zip
unzip master.zip

全基因组等位基因频率

为了根据群体基因组数据计算这些值，我们需要首先确定每个群体中基因组中每个多态性位点的衍生等位基因的频率。我们将根据使用 python 脚本提供的 Heliconius 基因型数据来计算这些值。输入文件已被过滤为仅包含双等位基因位点。频率脚本要求我们定义人群。这些在文件 hel92.pop.txt 中定义。

python genomics_general-master/freq.py -g data/hel92.DP8MP4BIMAC2HET75dist250.geno.gz \
-p mel_mel -p mel_ros -p mel_vul -p mel_mal -p mel_ama \
-p cyd_chi -p cyd_zel -p tim_flo -p tim_txn -p num \
--popsFile data/hel92.pop.txt --target derived \
-o data/hel92.DP8MP4BIMAC2HET75dist250.derFreq.tsv.gz

通过设置--target衍生，我们获得了每个位点每个群体中衍生等位基因的频率。这是基于使用指定的最终种群（H. numata silvana，或“slv”）作为外群。该种群对于祖先状态不固定的地点将被丢弃。

全基因组 ABBA BABA 分析

为了了解 ABBA BABA 测试的工作原理，我们将从头开始编写代码来进行测试。启动一个新的 R 脚本。这将使使用不同人群重新运行整个分析变得容易。

• 用于 ABBA BABA 分析的 R 函数

首先，我们定义一个函数来计算每个站点的 ABBA 和 BABA 比例，并使用它们来计算 D atstistic。输入将是群体 P1、P2 和 P3（即 p1、p1 和 p3）中派生等位基因的频率。 （外群中祖先等位基因的频率在所有位点都为 1，因为我们使用外群来识别祖先等位基因，因此可以忽略）。

D.stat <- function(p1, p2, p3) {
    ABBA <- (1 - p1) * p2 * p3
    BABA <- p1 * (1 - p2) * p3
    (sum(ABBA, na.rm=T) - sum(BABA, na.rm=T)) / (sum(ABBA, na.rm=T) + sum(BABA, na.rm=T))
    }

• 读入我们的等位基因频率数据。

freq_table = read.table("data/hel92.DP8MP4BIMAC2HET75dist250.derFreq.tsv.gz", header=T, as.is=T)

这创建了一个名为 freq_table 的对象，其中包含每个 SNP 的派生等位基因的频率。我们可以检查此表中的站点数量，还可以查看前几行以了解数据。

nrow(freq_table)

head(freq_table)

请注意，前两列给出了支架的名称（即染色体）和每个位点在染色体上的位置。其余列是不同亚种的等位基因频率，如上图所示。

• D 统计量

现在，为了计算 D，我们需要定义群体 P1、P2 和 P3。我们将从一个明显且先前发表的测试案例开始：我们将询问 H. melpomene rosina (mel_ros) 和 H. cydno chioneus (cyd_chi) 之间是否存在基因渗入的证据。它们分别是 P2 和 P3。 P1 将是我们的异种种群，来自法属圭亚那的 H. melpomene melpomene (mel_mel)。

我们设置这些群体，然后通过提取这三个群体的所有 SNP 的派生等位基因频率来计算 D。

P1 <- "mel_mel"
P2 <- "mel_ros"
P3 <- "cyd_chi"

D <- D.stat(freq_table[,P1], freq_table[,P2], freq_table[,P3])

print(paste("D =", round(D,4)))

我们得到的 D 统计量（记住 D 从 -1 到 1 变化），表明 ABBA 超过 BABA。这表明来自巴拿马的H. cydno chioneus (cyd_chi)与来自巴拿马的同域H. melpomene rosina (mel_ros)比与来自法属圭亚那的异体H. melpomene melpomene (mel_mel)有更多的遗传变异。这与同源的两个物种之间的杂交和基因流是一致的。

然而，我们目前不知道这个结果在统计上是否可靠。特别是，我们不知道过量的 ABBA 是否均匀分布在整个基因组中。如果它是由基因组某一部分的奇怪祖先造成的，我们就不太相信存在重大的入侵。

为了测试一致的全基因组信号，我们使用了block-jackknife程序。

• Block Jackknife

尽管站点之间不独立，但 Jackknife 允许我们计算 D 的方差。更传统的方法，即我们随机对位点进行重新采样并重新计算 D，是不合适的，因为基因组中附近的位点具有相似的祖先，使它们成为非独立的观察结果。

block jackknife 程序估计全基因组平均 D 的所谓“伪值”的标准偏差，其中每个伪值是通过排除基因组的定义块来计算的，取全基因组平均 D 和计算的 D 之间的差值当块被省略时。

为了考虑链接站点之间的非独立性，块大小需要超过发生自相关的距离。在我们的例子中，我们将使用 1 Mb 的块大小，因为我们知道连锁不平衡在远低于 1 Mb 的距离处衰减到背景水平。

运行 jackknife 过程的代码相当简单，但我们不打算在这里编写它。相反，用于此目的的 R 函数在单独的脚本中提供，我们现在可以导入该脚本。

source("genomics_general-master/jackknife.R")

该过程的第一步是定义在每次迭代中将从基因组中省略的块。 jackknife 脚本中的 get_block_indices 函数将执行此操作，并返回与每个块对应的“索引”（即频率表中的行）。它要求我们指定要分析的每个位点的块大小以及染色体和位置。

block_indices <- get.block.indices(block_size=1e6,
                                   positions=freq_table$position,
                                   chromosomes=freq_table$scaffold)

n_blocks <- length(block_indices)

print(paste("Genome divided into", n_blocks, "blocks."))

现在我们可以运行 block jackknifing 过程来计算 D 的平均值和标准误差。我们提供之前创建的 D 统计函数 (D.stat)，该函数将在每次迭代中应用。我们还提供每个站点的频率以及将用于从给定块中排除所有站点的块索引。

D_jackknife <- block.jackknife(block_indices=block_indices,
                               FUN=D.stat,
                               freq_table[,P1], freq_table[,P2], freq_table[,P3])

print(paste("D jackknife mean =", round(D_jackknife$mean,4)))

根据 D 的均值和标准误差的无偏估计，我们可以计算 Z 分数来测试 D 是否显着偏离零。

D_Z <- D_jackknife$mean / D_jackknife$standard_error

print(paste("D Z score = ", round(D_Z,3)))

通常，大于 3 或 4 的 Z 分数被视为显着，因此在这种情况下，大量 Z 分数意味着与零的偏差非常显着。

• 估计 admixture proportion

D 统计量为基因渗入提供了强有力的测试，但它并没有量化已共享的基因组的比例。已经开发出一种相关方法来估计“混合比例”f。

这种方法背后的想法是，我们将观察到的 ABBA 超过 BABA 位点的过量与完全混合下的预期进行比较。为了近似完全混合下的预期，我们重新计算 ABBA 和 BABA，但用 P3 物种的第二种群代替 P2。如果您缺乏第二个群体，您可以简单地将 P3 样本分成两部分。在本例中，我们有两个种群来代表每个物种，因此如果我们使用 H. cydno chioneus (cyd_chi) 作为 P3a，我们可以使用 H. cydno zelinde (cyd_zel) 作为 P3b)。

我们需要编写自己的函数来计算 f。输入将是每个群体中衍生的等位基因频率，但现在我们包括 P3a 和 P3b。

f.stat <- function(p1, p2, p3a, p3b) {
    ABBA_numerator <- (1 - p1) * p2 * p3a
    BABA_numerator <- p1 * (1 - p2) * p3a

    ABBA_denominator <- (1 - p1) * p3b * p3a
    BABA_denominator <- p1 * (1 - p3b) * p3a

    (sum(ABBA_numerator, na.rm=TRUE) - sum(BABA_numerator, na.rm=TRUE)) /
    (sum(ABBA_denominator, na.rm=TRUE) - sum(BABA_denominator, na.rm=TRUE))
    }

我们现在可以选择 P3a 和 P3b，并估计 f。

P3a <- "cyd_chi"
P3b <- "cyd_zel"

f <- f.stat(freq_table[,P1], freq_table[,P2], freq_table[,P3a], freq_table[,P3b])

print(paste("Admixture proportion = ", round(f,4)))

这表明，H. melpomene 和 H. cydno 的同源基因组中有超过 25% 的基因组是共享的。混合比例可以解释为任何单一基因组中外来血统的平均比例。或者，它可以解释为该群体中基因组中任何给定位点的外来等位基因的预期频率。

我们可以再次来估计f的标准差，并获得置信区间。 Jackknife 块索引已经计算出来，因此我们可以简单地再次运行 Jackknife 函数，这次将 f 函数指定为运行每次迭代的函数。

f_jackknife <- block.jackknife(block_indices=block_indices,
                               FUN=f.stat,
                               freq_table[,P1], freq_table[,P2], freq_table[,P3a], freq_table[,P3b])

95% 置信区间是平均值 +/- ~1.96 标准误差。

f_CI_lower <- f_jackknife$mean - 1.96*f_jackknife$standard_error
f_CI_upper <- f_jackknife$mean + 1.96*f_jackknife$standard_error

print(paste("95% confidence interval of f =", round(f_CI_lower,4), round(f_CI_upper,4)))

染色体 ABBA BABA 分析

• 所有染色体都显示基因渗入的证据吗？

上面，我们研究了整个基因组的基因渗入程度。假设每条染色体都有足够数量的 SNP，我们可以在染色体水平上进行类似的分析，以评估单个染色体上的渗入。

执行此操作的第一步是识别频率表中与 21 条 Heliconius 染色体中的每一条相对应的行。

我们首先使用 unique 函数识别数据集中存在的所有染色体名称。然后我们需要识别表中代表每条染色体的行。为此，我们使用 lapply 函数，该函数多次应用一个简单函数以创建 R 列表格式的组合输出。在这种情况下，我们将使用染色体名称来应用该函数，并且我们应用的函数将简单地询问表支架列中的哪些值对应于该染色体，利用 R which 函数。

chrom_names <- unique(freq_table$scaffold)
chrom_indices <- lapply(chrom_names, function(chrom) which(freq_table$scaffold == chrom))
names(chrom_indices) <- chrom_names

这将创建一个包含 21 个元素的列表 - 每个染色体对应一个元素。每个元素都是表中来自该染色体的所有位点的向量。我们可以通过对我们刚刚创建的列表应用长度函数来检查每个染色体有多少个 SNP。

sapply(chrom_indices, length)

（sapply 与 lapply 类似，只是它会尽可能简化输出，因此这里它返回一个向量，而不是向量列表）。

现在我们可以使用这些索引来计算每个染色体的 D 值。我们再次使用 sapply，这次应用 D.stat 函数并仅对每种情况下来自特定染色体的表中的行进行索引。

D_by_chrom <- sapply(chrom_names,
                     function(chrom) D.stat(freq_table[chrom_indices[[chrom]], P1],
                                            freq_table[chrom_indices[[chrom]], P2],
                                            freq_table[chrom_indices[[chrom]], P3]))

我们还需要来确定每个染色体的 D 是否与零显着不同。首先，我们将定义用于每个染色体的块。

block_indices_by_chrom <- sapply(chrom_names,
                                 function(chrom) get.block.indices(block_size=1e6,
                                                                   positions=freq_table$position[freq_table$scaffold==chrom]),
                                                                   simplify=FALSE)

此命令返回列表的列表。这是一个包含 21 个元素的列表 - 每条染色体一个。每个元素都是一个列表，给出该染色体内每个块的索引。

我们可以检查每条染色体的块数，以及每条染色体每个块的 SNP 数量。

sapply(block_indices_by_chrom, length)

lapply(block_indices_by_chrom, sapply, length)

现在我们使用折刀计算每个染色体 D 的 Z 分数。

D_jackknife_by_chrom <- sapply(chrom_names,
                                 function(chrom) block.jackknife(block_indices=block_indices_by_chrom[[chrom]],
                                                                 FUN=D.stat,
                                                                 freq_table[chrom_indices[[chrom]], P1],
                                                                 freq_table[chrom_indices[[chrom]], P2],
                                                                 freq_table[chrom_indices[[chrom]], P3]))

D_jackknife_by_chrom <- as.data.frame(t(D_jackknife_by_chrom))

D_jackknife_by_chrom$Z <- as.numeric(D_jackknife_by_chrom$mean) / as.numeric(D_jackknife_by_chrom$standard_error)

D_jackknife_by_chrom

我们看到 1-20 号染色体均显示出显着的渐渗证据（Z > 4），而 21 号染色体（Z 性染色体）则没有。事实上，chr21 的 D 为负值，表明异域 H. melpomene 种群与 H. cydno 的变异多于同域 H. melpomene 与 H. cydno 的变异，尽管差异并不显着。这表明与基因组的其余部分相比，性染色体上的基因渗入显着减少，这与针对性染色体上基因渗入的等位基因的强烈选择一致。如果存在一种或多种不相容性导致涉及 Z 染色体上的基因座，这就是我们所期望的。

Reference

[1]

Source: https://github.com/simonhmartin/tutorials/blob/master/ABBA_BABA_whole_genome/README.md

本文由 mdnice 多平台发布