八大排序源码（含优化）

大家好，我是纪宁，这篇文章是关于八大排序的源代码，具体实现过程会在后续文章中介绍。

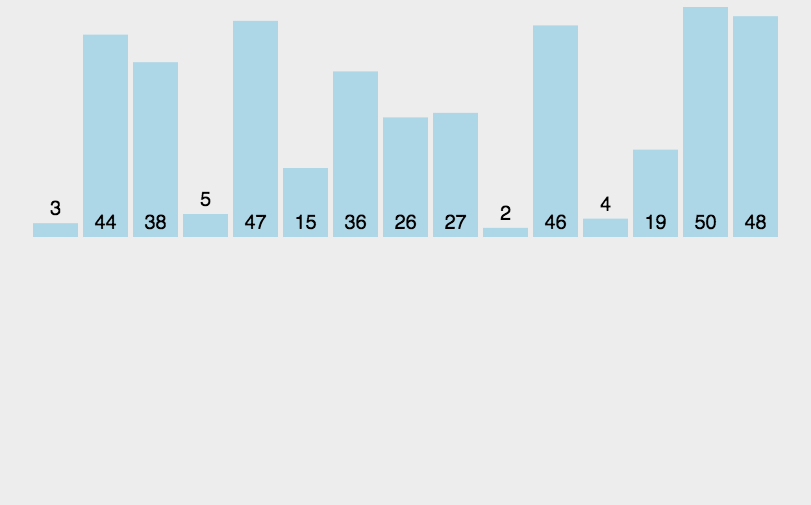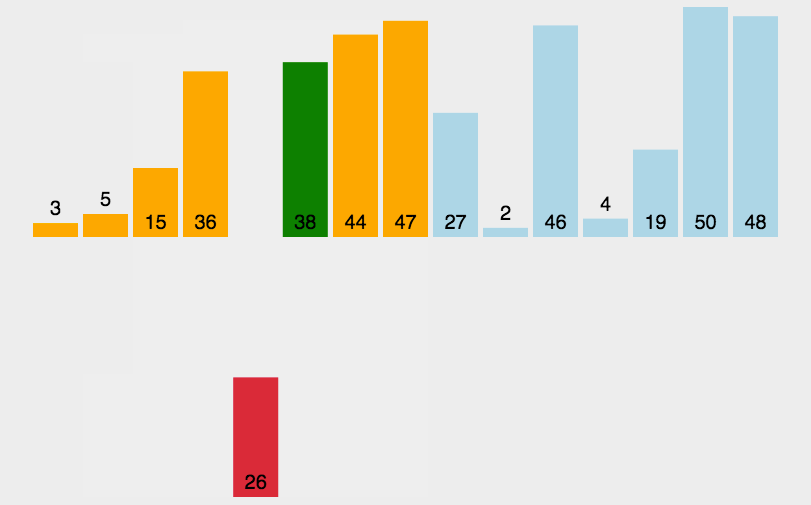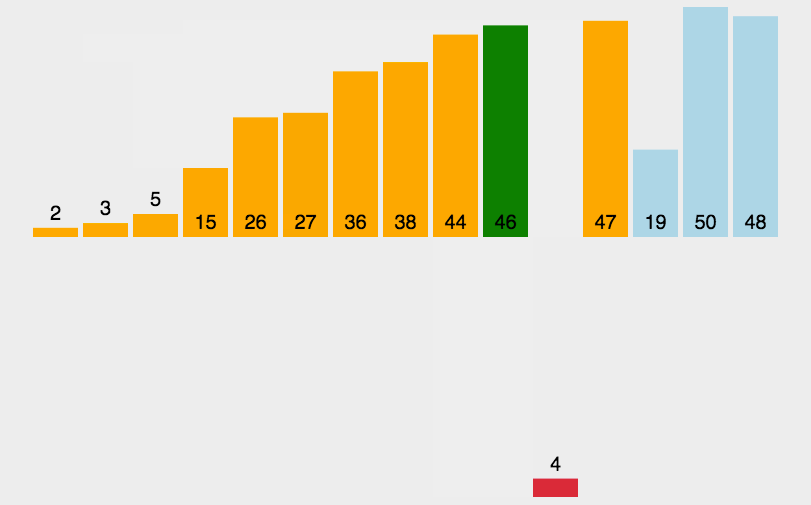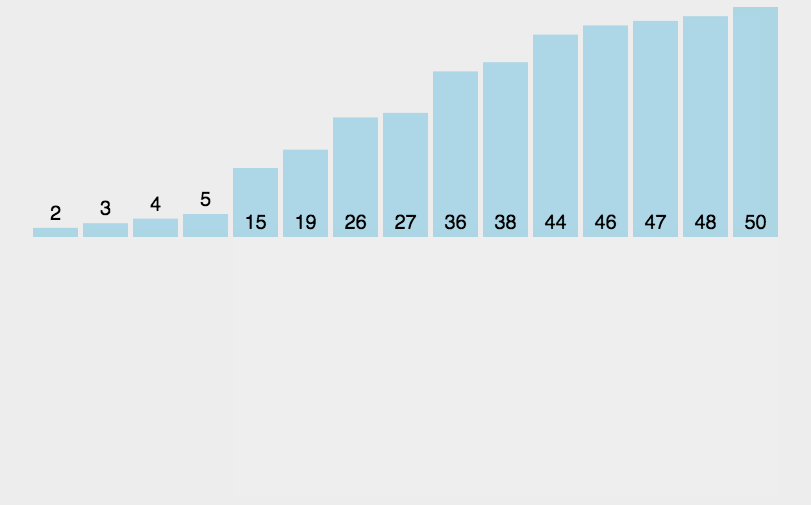
1、直接插入排序

时间复杂度O(N^2)，原数据越有序，效率越高。
当原数据有序时，则时间复杂度为O(N)。原数据倒序时，时间复杂度为O(N^2)

void InsertSort(int* a, int n)//直接插入排序
{
	for (int i = 0; i < n - 1; i++)
	{
		int end = i;
		int tmp = a[end+1];
		while (end >= 0)
		{
			if (a[end] >tmp)
			{
				a[end + 1] = a[end];
			}
			else
			{
				break;
			}
			end--;
		}
		a[end + 1] = tmp;
	}
}

2、希尔排序

时间复杂度：O(N*logN) 空间复杂度：O(1)
希尔排序是插入排序的优化，整体思路是先预排序，使原数据更接近有序，等到gap==1时，就变成了直接插入排序。

void ShellSort(int* arr, int n)
{
	int gap = n;
	while (gap > 1)
	{
		gap = gap / 3 + 1;//gap也可以 /=2；奇特数字必须保证gap最后的值为1
		for (int i = 0; i < n - gap; i++)
		{
			int end = i;
			int tmp = arr[end + gap];
			while (end >= 0)
			{
				if (tmp < arr[end])
				{
					arr[end + gap] = arr[end];
				}
				else
				{
					break;
				}
				end -= gap;
			}
			arr[end + gap] = tmp;
		}
	}
}

3、选择排序

时间复杂度：O(N^2) 空间复杂度：O(1)
每次选择一个最大或者最小的数，使其出现在正确的位置。

void SelectSort(int* a, int n)
{
	for (int j = 0; j < n; j++)
	{
		int mini = j;
		int maxi= n - j-1;
		for (int i = j; i < n-j; i++)
		{
			if (a[i] < a[mini])
			{
				mini = i;
			}
			if (a[i] > a[maxi])
			{
				maxi = i;
			}
		}
		Swap(&a[mini], &a[j]);
		if (maxi == j)
		{
			maxi = mini;//最大值如果在 j 这个位置的话，结果这个位置被换成了min 的值
		}
		Swap(&a[maxi], &a[n-1-j]);
	}
}

4、冒泡排序

时间复杂度：O(N^2) 空间复杂度：O(1)
思路最简单的排序，所有程序员的白月光！

void BubbleSort(int* a, int n)//冒泡排序
{
	for (int i = 0; i < n; i++)
	{
		int ret = 0;//如果一趟后ret还等于0，说明数据已经有序
		for (int j = 0; j < n - i - 1; j++)
		{
			if (a[j] > a[j + 1])
			{
				Swap(&a[j], &a[j + 1]);
				ret = 1;
			}
		}
		if (ret == 0)
			break;
	}
}

5、堆排序

时间复杂度：O(N*logN) 空间复杂度：O(1)
建堆的时候可以采用向上调整和向下调整建堆，而排序的时候只能使用向下调整算法。
排升序建大堆，降序建小堆。

void Adjustup(int* a, int child)//向上调整
{
	int parent = (child - 1) / 2;
	while (parent >= 0)
	{
		if (a[child] > a[parent])
		{
			Swap(&a[child], &a[parent]);
			child = parent;
			parent = (child - 1) / 2;
		}
		else
		{
			break;
		}
	}
}

void Adjustdown(int* a, int parent, int n)//向下调整
{
	int child = 2 * parent + 1;
	while (child < n)
	{
		if (child + 1 < n && a[child + 1] > a[child])
		{
			child++;
		}
		if (a[child] > a[parent])
		{
			Swap(&a[child], &a[parent]);
			parent = child;
			child = 2 * parent + 1;
		}
		else
		{
			break;
		}
	}
}

void HeapSort(int* arr, int sz)
{
	//第一步，建堆
	向上调整建堆
	
	//for (int i = 1; i < sz; i++)
	//{
	//	Adjustup(arr, i); 
	//}
	//向下调整建堆

	for (int i = (sz - 1) / 2; i >= 0; i--)
	{
		Adjustdown(arr, i, sz - 1);
	}
	int end = sz - 1;
	while (end > 0)
	{
		Swap(&arr[0], &arr[end]);
		Adjustdown(arr, 0, end);
		end--;
	}
}

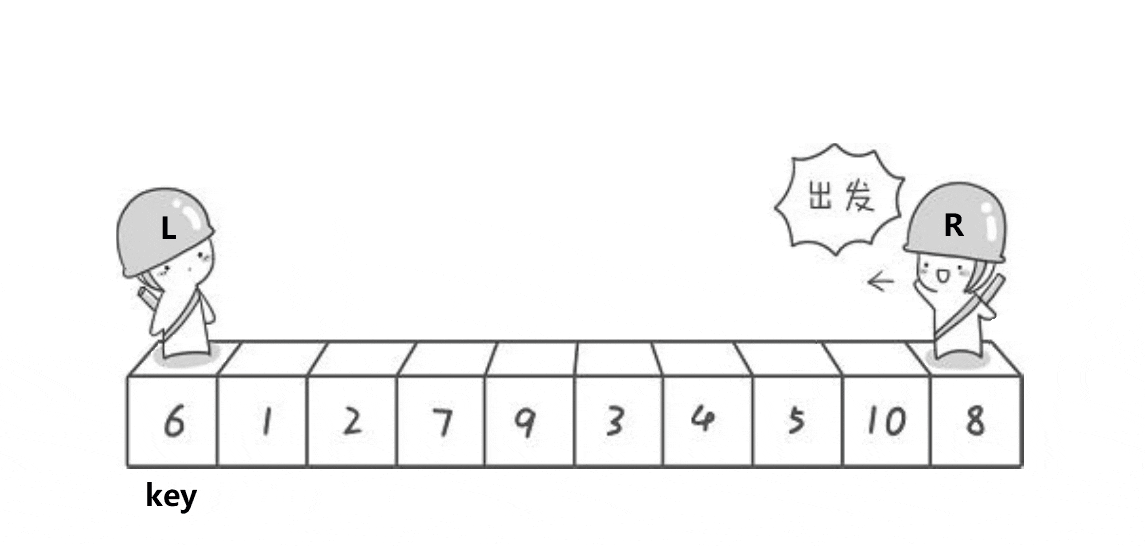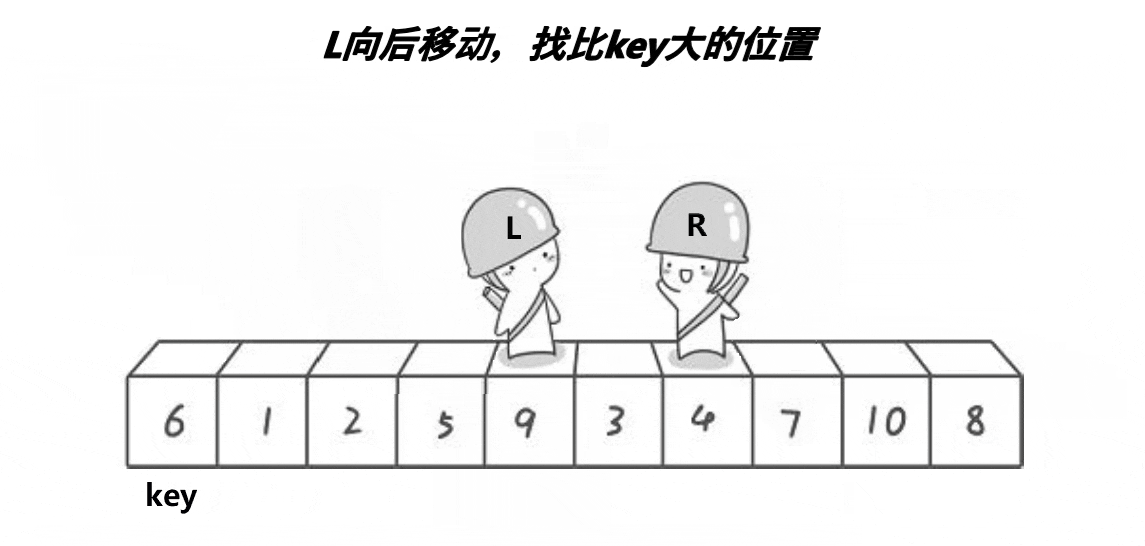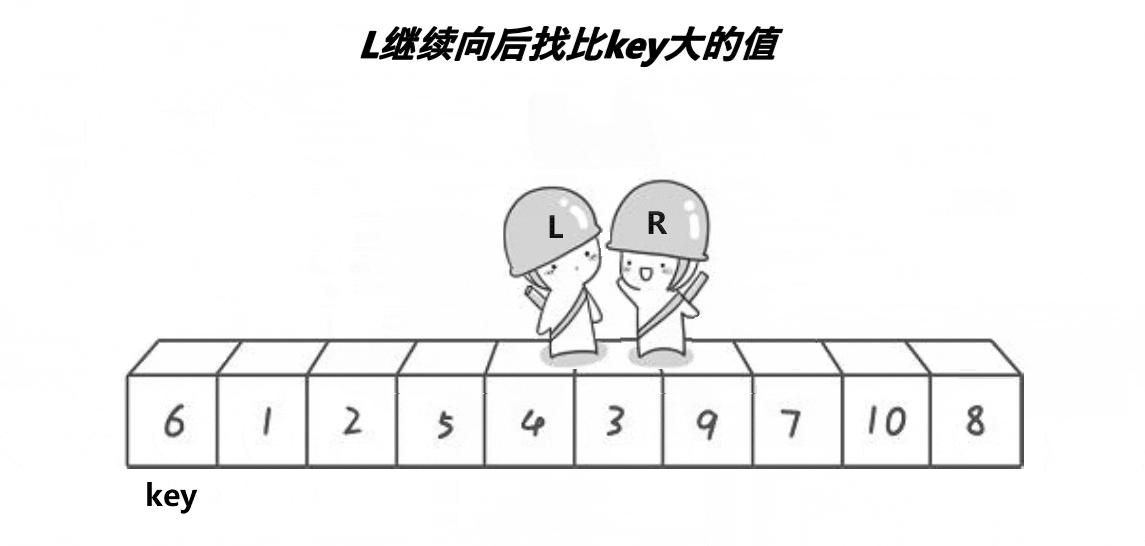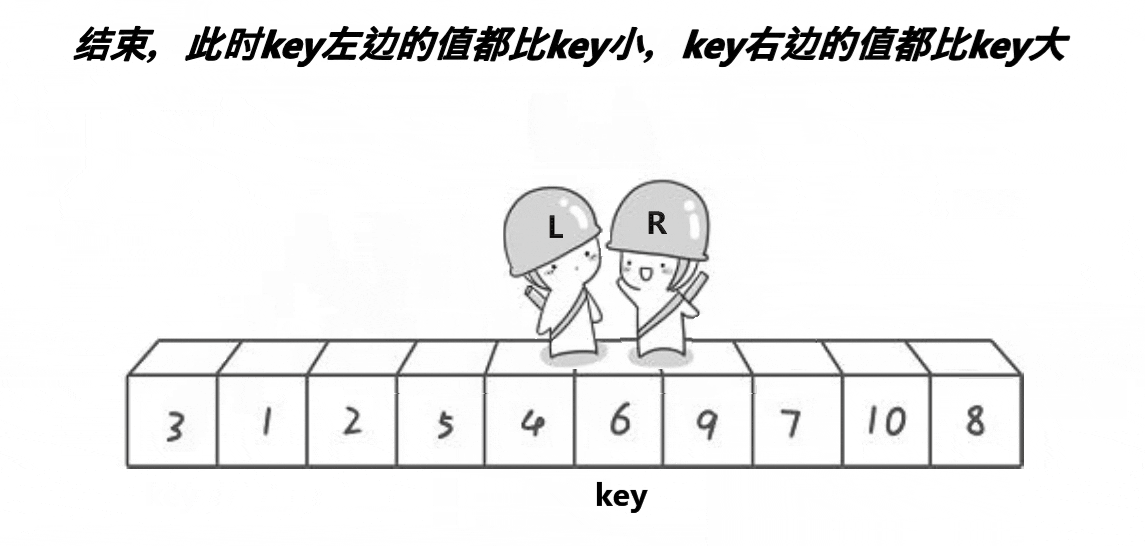
6、快速排序

时间复杂度：O(N*logN) 空间复杂度：O(1)

快速排序递归实现

霍尔法

int QuickSortPart1(int*a,int left,int right)//霍尔版本
{
	int* Maxi = (&a[left], &a[right], &(a[(left + right) / 2]));//三数取中
	Swap(&a[left], Maxi);//换到最左边
	int key = a[left];
	int keyi = left;
	while (left<right)
	{
		while (left<right && a[right]>=key)
		{
			right--;
		}
		while (left < right && a[left] <= key)
		{
			left++;
		}
		Swap(&a[left], &a[right]);
	}
	Swap(&a[keyi], &a[left]);
	return left;
}
void QuickSort(int*arr, int begin, int end)
{
	if (begin >= end)//等于是只有一个数需要排，大于是没有数需要排
	{
		return;
	}
	int keyi = QuickSortPart1(arr, begin, end);
	/*int keyi = QuickSortPart2(arr, begin, end);
	int keyi = QuickSortPart3(arr, begin, end);*/
	QuickSort(arr, begin, keyi - 1);
	QuickSort(arr, keyi + 1, end);
}

挖坑法

int QuickSortPart2(int* arr, int left, int right)//挖坑法
{
	int* Maxi = (&arr[left], &arr[right], &(arr[(left + right) / 2]));
	Swap(&arr[left], Maxi);
	int holei = left;
	int hole = arr[left];
	while (left < right)
	{
		while (left < right && arr[right] >= hole)
		{
			right--;
		}
		arr[holei] = arr[right];
		holei = right;
		while (left < right && arr[left] <= hole)
		{
			left++;
		}
		arr[holei] = arr[left];
		holei = left;
	}
	arr[holei] = hole;
	return left;
}
void QuickSort(int*arr, int begin, int end)
{
	if (begin >= end)//等于是只有一个数需要排，大于是没有数需要排
	{
		return;
	}
	/*int keyi = QuickSortPart1(arr, begin, end);*/
	int keyi = QuickSortPart2(arr, begin, end);
	/*int keyi = QuickSortPart3(arr, begin, end);*/
	QuickSort(arr, begin, keyi - 1);
	QuickSort(arr, keyi + 1, end);
}

前后指针法

int QuickSortPart3(int* a, int left, int right)//快排快慢指针
{
	int* Maxi = (&a[left], &a[right], &(a[(left + right) / 2]));
	Swap(&a[left], Maxi);
	int keyi = left;
	int prev = left;
	int cur = left+1;
	while (cur <= right)
	{
		if (a[cur] < a[keyi]&& ++prev!= cur)
		{
			Swap(&a[prev], &a[cur]);
		}
		cur++;
	}
	Swap(&a[prev],&a[keyi]);
	return prev;
}

void QuickSort(int*arr, int begin, int end)
{
	if (begin >= end)//等于是只有一个数需要排，大于是没有数需要排
	{
		return;
	}
	//*int keyi = QuickSortPart1(arr, begin, end);*/
	//int keyi = QuickSortPart2(arr, begin, end);
	int keyi = QuickSortPart3(arr, begin, end);
	QuickSort(arr, begin, keyi - 1);
	QuickSort(arr, keyi + 1, end);
}

快速排序小区间优化

void QuickSort1(int* a, int begin, int end)
{
	if (begin >= end)
		return;

	// 小区间优化，小区间不再递归分割排序，降低递归次数
	if ((end - begin + 1) > 10)
	{
		int keyi = PartSort3(a, begin, end);

		// [begin, keyi-1] keyi [keyi+1, end]
		QuickSort1(a, begin, keyi - 1);
		QuickSort1(a, keyi + 1, end);
	}
	else
	{
		InsertSort(a + begin, end - begin + 1);//直接插入排序
	}
}

快速排序非递归实现

快排非递归要用栈来实现

void QuickSortNorn(int* a, int begin, int end)
{
	ST st;//创建数组栈
	STInit(&st);//初始化栈
	STPush(&st, end);//入栈
	STPush(&st, begin);//入栈
	while (!STEmpty(&st))//判空
	{
		int left = STTop(&st);//取栈顶数据
		STPop(&st);//出栈
		int right = STTop(&st);
		STPop(&st);

		int keyi = QuickSortPart1(a, left,right);
		if (keyi + 1 < right)
		{
			STPush(&st, right);
			STPush(&st, keyi + 1);
		}
		if (keyi - 1 > left)
		{
			STPush(&st, keyi - 1);
			STPush(&st, left);
		}
	}
	STDestroy(&st);//销毁栈
}

7、归并排序

时间复杂度：O(N*logN) 空间复杂度：O(N)

归并排序递归实现

void _MergeSortPart(int* a, int* tmp, int begin, int end)
{
	if (begin >= end)
		return;
	int midi = (begin + end) / 2;
	_MergeSortPart(a, tmp, begin, midi);
	_MergeSortPart(a, tmp, midi + 1, end);
	int begin1 = begin, end1 = midi;
	int begin2 = midi + 1, end2 = end;
	int index = begin;
	while (begin1 <= end1 && begin2 <= end2)
	{
		if (a[begin1] < a[begin2])
		{
			tmp[index++] = a[begin1++];
		}
		else
		{
			tmp[index++] = a[begin2++];
		}
	}
	while (begin1 <= end1)
	{
		tmp[index++] = a[begin1++];
	}
	while (begin2 <= end2)
	{
		tmp[index++] = a[begin2++];
	}
	memcpy(a+begin, tmp+begin, sizeof(int) * (end - begin + 1));
}
void MergeSort(int* a, int n)
{
	int* tmp = (int*)malloc(sizeof(int) * n);
	_MergeSortPart(a, tmp, 0, n - 1);
	free(tmp);
	tmp = NULL;
}

归并排序非递归

void _MergeSortNonr(int* a, int* tmp, int begin, int end)
{
	int gap = 1;
	while (gap <= end)
	{
		for (int i = 0; i <= end; i += 2 * gap)
		{
			int begin1 = i, end1 = i + gap - 1;
			int begin2 = i + gap, end2 = i + 2 * gap - 1;
			int index = i;
			if (begin2 > end)
			{
				break;
			}
			if (end2 > end)
			{
				end2 = end;//对范围进行修正
			}
			while (begin1 <= end1 && begin2 <= end2)
			{
				if (a[begin1] < a[begin2])
				{
					tmp[index++] = a[begin1++];
				}
				else
				{
					tmp[index++] = a[begin2++];
				}
			}
			while (begin1 <= end1)
			{
				tmp[index++] = a[begin1++];
			}
			while (begin2 <= end2)
			{
				tmp[index++] = a[begin2++];
			}
			memcpy(a + i, tmp + i, sizeof(int) * (end2-i+1));//拷贝回原数组
		}
	gap *= 2;
	}
	 
}
void MergeSortNonr(int* a, int n)//归并排序非递归
{
	int* tmp = (int*)malloc(sizeof(int) * n);
	_MergeSortNonr(a, tmp, 0, n - 1);
	free(tmp);
	tmp = NULL;
}

8、计数排序

时间复杂度：O(MAX(N,range)) 空间复杂度：O(range)

void CountSort(int* a, int n)//计数排序
{
	//先找最大值和最小值
	int maxi = 0, mini = 0;
	for (int i = 1; i < n; i++)
	{
		if (a[i] > a[maxi])
		{
			maxi = i;
		}
		if (a[i] < a[mini])
		{
			mini = i;
		}
	}
	int max = a[maxi], min = a[mini];
	int range = a[maxi] - a[mini]+1;
	int* count = (int*)malloc(sizeof(int) * range);
	memset(count, 0, sizeof(int) * range);
	for (int j = 0; j < n; j++)
	{
		count[a[j] - min]++;
	}
	int i = 0;
	for (int j = 0; j < n; j++)
	{
		while (count[j]--)
		{ 
			a[i++] = j + min;
		}
	}
}