C/C++ 位操作符“&” “|” “^”巧妙应用♥
目录
前言
一、按位与&
二、按位或 |
三、按位异或 ^
总结
前言
学习C语言,必不可少的就是学习操作符。
C语言共有如下操作符:
C语言各类操作符的优先级如下表:
本文主要来介绍,不太起眼,有时又能帮上大忙的操作符“位操作符”,以及“移位操作符”
纯纯干货,有兴趣的话继续往下看吧!
一、按位与 &
0 & 0 = 0 ; 0 & 1 = 0; 1 & 0 = 0; 1 & 1 = 1;
总结: 有 0 为 0 ;全 1为 1;
那么在C语言是如何体现的呢!
我们知道在32位计算机中,一个整型是以32位二进制进行存储的;
int n = 11 ;在计算机中 0000 0000 0000 0000 0000 0000 0000 1011;进行存储
int m = 10; 在计算机中 0000 0000 0000 0000 0000 0000 0000 1010;进行存储
int ans = n&m ;就是32位中的每一位对应进行&运算结果为
int ans = n&m ;在计算机中 0000 0000 0000 0000 0000 0000 0000 1010; 进行存储
特别注意的是负数,负数的是以补码的形式进行存储!
例如 : -1
原码 :1000 0000 0000 0000 0000 0000 0000 0001
反码 :1111 1111 1111 1111 1111 1111 1111 1110
补码 :1111 1111 1111 1111 1111 1111 1111 1111
所以可以得出任何数 &(-1)都等于它本身;
学会了&按位与的过程,思考一个小问题:如何求得一个数的二进制有几个1。
正常的思路就是十进制转换二进制的过程:除以2取余数,在整除2;这么写的代码如下:
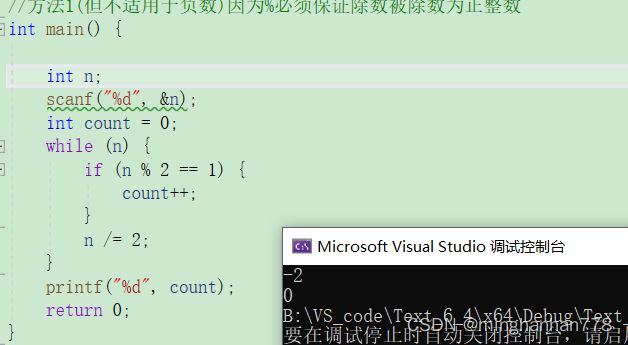
方法1(但不适用于负数)因为%必须保证除数被除数为正整数
#include
int main() {
int n;
scanf("%d", &n);
int count = 0;
while (n) {
if (n % 2 == 1) {
count++;
}
n /= 2;
}
printf("%d", count);
return 0;
}
其中运用到了%取余运算符,但是取余运算符是有局限的不能对负数进行取余;
输入-2 得出来的结果为0;
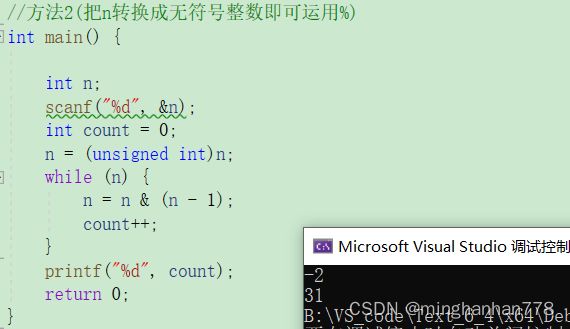
这时候肯定有小聪明冒出来啦,把-2转换成无符号整型就可以完成,确实是一种好的思路,代码如下:
//方法2(把n转换成无符号整数即可运用%)
#include
int main() {
int n;
scanf("%d", &n);
int count = 0;
n = (unsigned int)n;
while (n) {
n = n & (n - 1);
count++;
}
printf("%d", count);
return 0;
}
-2
原码 :1000 0000 0000 0000 0000 0000 0000 0010
反码 :1111 1111 1111 1111 1111 1111 1111 1101
补码 :1111 1111 1111 1111 1111 1111 1111 1110
所以结果正确,有31个1,思路正确!
在这里运用&按位与提供第三种方法来计算二进制有几位 1 ;
思路如下:
//方法3
int main() {
int n;
scanf("%d", &n);
int count = 0 ;
while (n) {
n = n & (n - 1);
count++;
}
printf("%d", count);
return 0;
}
例如n = 11;
n = 1011 n-1 = 1010 一次
n = 1010 n-1 = 1001 二次
n = 1000 n-1 = 0111 三次
n = 0000 结束 while
理解:每一次循环就可以去掉一个1,所以循环几次就可以知道有几个1通过 n&(n-1)我们可以去掉最后一位的1;
这种方式不仅可以适用于负数,而且计算机运行速度更快,效率更高!
请把“学到了打在公屏上!”♥
二、按位或 |
0 | 0 = 0 ; 0 | 1 = 1 ; 1 & 0 = 1 ; 1 | 1 = 1 ;
总结:有 1 为 1 ,全 0 为 0 ;
类比 & 做一个简单的模仿 ;
int n = 11 ;在计算机中 0000 0000 0000 0000 0000 0000 0000 1011;进行存储
int m = 10; 在计算机中 0000 0000 0000 0000 0000 0000 0000 1010;进行存储
int ans = n | m ;就是32位中的每一位对应进行 | 运算结果为
int ans = n | m ;在计算机中 0000 0000 0000 0000 0000 0000 0000 1011; 进行存储
三、按位异或 ^
0 ^ 0 = 0 ; 0 ^ 1 = 1; 1 ^ 0 = 1 ; 1 ^ 1 = 0 ;
总结 : 相同为 0 ,不同为 1 ;
类比 & 做一个简单的模仿 ;
int n = 11 ;在计算机中 0000 0000 0000 0000 0000 0000 0000 1011;进行存储
int m = 10; 在计算机中 0000 0000 0000 0000 0000 0000 0000 1010;进行存储
int ans = n ^ m ;就是32位中的每一位对应进行 ^ 运算结果为
int ans = n ^ m ;在计算机中 0000 0000 0000 0000 0000 0000 0000 0001; 进行存储
有了 & | ^ 的基础,思考一个问题,如何求解两个整型n ,m 的二进制有几位不!
思路:int ans = n ^ m 的结果中,不同的为1 ,相同的为0;所以只要求得ans有几个1即可,所以问题又回到了求一个整型有几个1 ;
代码如下:
(32位)两个数的二进制位,有几位不同(两个方法,用&与 ^异或
方法1 ^异或法
#include
int main() {
int m, n;
scanf("%d%d", &m, &n);
int ans = 0;
int count = 0;
ans = m ^ n;//m,n,二进制位相同的为0,不同的位1,赋给了k所以只要知道k有几个1即可
while (ans) {//问题转化为一个数的二进制有几位1
ans = ans & (ans - 1);
count++;
}
printf("有%d位不同", count);
return 0;
} 方法2 :我们可以不用^异或,我们可以只用&按位与;
思路:n&1的结果就是n的第一位二进制数,m&1就是m的第一位二进制数,然后我们判断相不相等,然后将n与m向右移一位继续判断,循环32次即可!代码如下:
方法2 按位与 & 1 能得出第一位是0还是1,然后在将数同时向右移动一位继续比即可
#include
int main() {
int n, m;
scanf("%d%d", &n, &m);
int count = 0;
for (int i = 0; i < 32; i++) {
if (((n >> i) & (1)) != ((m >> i) & (1))) {
count++;
}
}
printf("有%d位不同", count);
return 0;
}
再思考一个小问题:如何实现两个变量交换数值;问题很简单,但是如果加上不能设置第三变量的条件又如何实现呢?
方法1:
int n = 2 ;
int m = 3;
n = m + n ;
m = n - m ;
n = n - m ;
这个方法确实可行但是 进行第一步的时候,有可能会超出 int 的范围,有一定的风险!
方法2 :三异或
#include
int main()
{
int a = 10;
int b = 20;
a = a^b;
b = a^b;
a = a^b;
printf("a = %d b = %d\n", a, b);
return 0;
} a 0000 0000 0000 0000 0000 0000 0000 1010
b 0000 0000 0000 0000 0000 0000 0001 0100
a1 0000 0000 0000 0000 0000 0000 0001 1110
b1 0000 0000 0000 0000 0000 0000 0000 1010 = a
a2 0000 0000 0000 0000 0000 0000 0001 0100 = b
这个方法,思路很清奇,也的确避免了越界的可能,希望大家能够接收!
总结
按位与 或 异或,在平常使用的频率不会很高,当要在实现二进制的功能时会有意想不到的结果,希望大家能够吸收下去,奥里给♥