Simulink卡尔曼滤波系统建模实例——高度解算融合
前言
这个项目主要是利用加速度计和气压计作为输入,经过卡尔曼滤波融合后输出高度、速度、加速度,这三个输出量对于产品的某执行机构来说需要满足符合无人机飞行特征,而这个项目也是基于原算法在Simulink上面的复现以及优化。
void update_sys() {
X_hat = F * X;
P_hat = F * P * F.transpose() + Q;
P_inv = H * P_hat * H.transpose() + R;
K = P_hat * H.transpose() * inv(P_inv);
X = X_hat + K * (Y - H * X_hat);
P = (I - K * H) * P_hat;
}
算法模型
算法原理
KF实际意义上是最优化递归数字处理算法(Optimal Recursive Data Processing Algorithm)。在变化的数据中去除噪声对系统未来输出做出预测的算法,是基于概率统计原理的预测算法,算法输入的量是可测的(例如我的实例中的输入就用到了加速度计和气压计测量出来的数据),并且还知道这个测量值的精度大概在多少,有了这个测量值我们就根据测量值来估计这个系统的真实输出,并同时给出我新估计的这个值的精度大概在什么范围内,这就是卡尔曼滤波做的工作,但这个工作是不断进行的,对系统不断测量,然后不断估计,这样持续一段时间之后就能估计出系统一个非常准确的输出值。这里要明确的一点是,测量值可能非常不准确,估计值也非常不准确,这符合工程中的很多工作状况,但仅仅根据这两个不准确的值最后就可以估计出一个相对准确的系统输出值,这也就是卡尔曼滤波的作用。
算法五个重要公式
预测过程:

校正过程:

(这里对公式推导就不做太多的赘述了,因为这篇讲的是Simulink卡尔曼滤波系统建模。)
Simulink模块化建模
Subsystem
利用SubSystem对每一个公式建立一个子系统进行计算以及数据的传递。这样的好处就是可以对每个公式进行单元测试,即在仿真过程中对数据的可处理性比较好。
完整模型图

不难看出,其实利用子模块搭建的话对线的布局是有点杂乱的,后面会说到一个更优化的方案S-Function-Builder进行替代。
预测
校正(更新)
滤波增益(对应公式三):
这里我把它拆分成了两个模块:单独一个模块计算取逆,另外一个模块是计算滤波增益的。


状态更新(对应公式四):
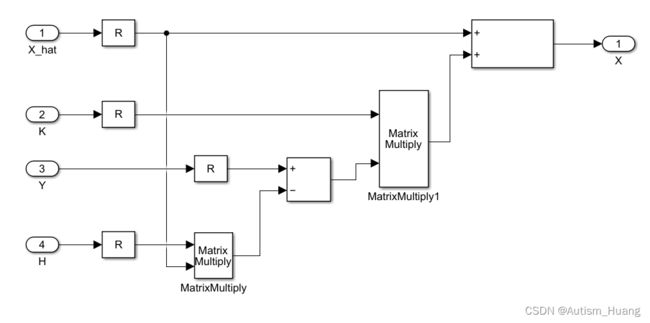
协方差更新(对应公式五):

总结
这里的子系统输入都有一个Reshape模块对输入的数据进行重构成目标矩阵,如果需要初始化变量的话可以用一个IC模块初始化输入(IC模块只是在模型执行的第一个步长输入,后续会按原反馈输入),对于数据我们可以利用数据字典sldd对信号线进行绑定,然后可以在Model Explorer选项中将sldd中的数据的Code Generation中设置成外部调用的全局变量,这样在生成嵌入式代码的时候变量也能很好地被调用。在连接反馈回路的时候,对于直接馈通的信号,是需要加一个one step delay模块的,不然就会产生代数环并且无法生成嵌入式代码,因为模型执行是所有模块一起同时计算的,在有反馈的控制系统中,也是必须遵循因果系统的。
S-Function-Builder
一开始我是用S-Function进行建模仿真的,在仿真完后想生成嵌入式代码烧录进芯片里面却发现无法生成嵌入式代码,然后就只能用S-Function-Builder代替了。其实在2021版的Simulink用S-Function-Builder比以前的版本方便很多了,但是也有一些无缘无故的坑,比如导入库或者调用头文件的时候,编译代码会报错,修改路径也无济于事,然后重启软件居然就又可以了。先上完整模型图。
完整模型图
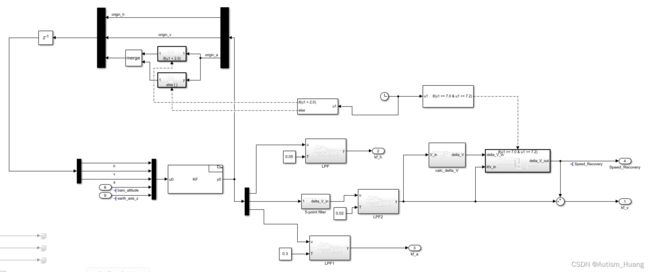
看起来是不是比单纯的子系统建模好看多了,反正我是这么觉得的。算法模型是完全在S-Function-Builder里面实现的,用的是.c文件。
主要的算法实现是在(S-FunctionName)_Outputs_wrapper函数中实现的。
void KF_Outputs_wrapper(const real32_T *u0,real32_T *y0)
{
/* Output_BEGIN */
// Update Data
X[0] = u0[0];
X[1] = u0[1];
X[2] = u0[2];
Y[0] = u0[3];
Y[1] = u0[4];
/* Calc Start */
// X_hat = F * X;
matrix_mul(3,3,1,F,X,X_hat);
// P_hat = F*P*F_T + Q;
matrix_mul(3,3,3,F,P,FP);
matrix_mul(3,3,3,FP,FT,FPFT);
matrix_add(3,3,FPFT,Q,P_hat);
// P_inv = H*P_hat*H_T + R;
matrix_mul(2,3,3,H,P_hat,HPhat);
matrix_mul(2,3,2,HPhat,HT,HPhatHT);
matrix_add(2,2,HPhatHT,R,P_inv);
// K = P_hat*H_T*inv_P;
Gauss((float(*)[2])P_inv, (float(*)[2])inv_P, 2);
matrix_mul(3,3,2,P_hat,HT,PhatHT);
matrix_mul(3,2,2,PhatHT,inv_P,K);
// X = X_hat + K*(Y - H*X_hat);
matrix_mul(2,3,1,H,X_hat,HXhat);
matrix_sub(2,1,Y,HXhat,Y_HX);
matrix_mul(3,2,1,K,Y_HX,KY);
matrix_add(3,1,X_hat,KY,X);
// P = (I - K*H) * P_hat;
matrix_mul(3,2,3,K,H,KH);
matrix_sub(3,3,I,KH,I_KH);
matrix_mul(3,3,3,I_KH,P_hat,P);
y0[0] = X[0];
y0[1] = X[1];
y0[2] = X[2];
/* Output_END */
}
系统的输入是u,输出是y。
总结
整个模型相比于由子系统模块搭建的模型来说直观了很多,不用绕很多圈子来计算最后的输出量。,利用S-Function-Builder生成的代码实现的结果与原算法的结果基本相似,所以在优化上面我采取了滤波以及速度补偿。在KF算法中,融合出来的速度跟期望的基准是存在误差的,无论是Q还是R都是会有影响,因此在满足数据不发散并且是可信的前提下,我对速度进行了速度补偿,即初始化的时候以0为基准。同时因为加速度计数据抖动十分明显,所以在反馈通路的前置加入了一个加权递推滤波算法,在后置加入了一个LPF对输出的数据进行处理,对振荡的抑制效果尤为明显,虽然滤波会对数据与原数据产生相位的偏差(响应变慢),但是站在数据可信度的角度出发,我会牺牲一点响应来换取数据的可信度。

