最大信息系数(MIC)——大数据时代的相关性分析

在信息爆炸的当今社会，单靠人力已经不能在无穷无尽的数据中有效的捕获信息。数据挖掘这一学科的兴起也预示着在各行业即将展开一场数据革命。在大数据集中识别两个变量的相关关系越来越重要。数据的相关性又分为线性相关和非线性相关。

利用Pearson相关系数或者Spearman相关系数等可以有效的度量数据的线性相关性，甚至可以通过回归分析确定线性关系和简单非线性关系的数学公式。然而由于自然规律的复杂性，现实世界中的数据之间即使有较强的相关关系，绝大多数也是非线性的而且无法用简单的数学公式表达。为了度量数据间非线性相关性的强弱，科学家们提出了基于阀值相关、相位同步相关、距离相关、互信息等的度量方法。最大信息系数（The Maximal Information Coefficient，MIC）是在互信息的基础上发展起来的，MIC方法能快速通过给不同类型的关联关系进行评估，从而发现广泛范围的关系类型，此算法的作者来自哈佛大学，并在生物学等数据上进行了成功的实验，相关成果公布在Science杂志上。

MIC的优越性

根据MIC的性质，MIC具有普适性、公平性和对称性。所谓普适性，是指在样本量足够大(包含了样本的大部分信息)时，能够捕获各种各样的有趣的关联，而不限定于特定的函数类型(如线性函数、指数函数或周期函数)，或者说能均衡覆盖所有的函数关系。一般变量之间的复杂关系不仅仅是通过单独一个函数就能够建模的，而是需要叠加函数来表现。所谓公平性，是指在样本量足够大时能为不同类型单噪声程度相似的相关关系给出相近的系数。例如，对于一个充满相同噪声的线性关系和一个正弦关系，一个好的评价算法应该给出相同或相近的相关系数。

MIC与具有代表性的六种相关性评价算法的普适性对比如下图所示，可以看出MIC不仅可以检测出线性关系，还能够检测出各种非线性关系，并且只要两个变量不独立，它们的MIC系数均为1；而其他评价方法或者只适合检测线性关系，或者没有标准化，或者无法检测出正弦关系、周期性关系等。如果采用没有普适性的算法进行相关性挖掘，那么结果就不是完备的，会令人漏掉许多有用的关联关系。

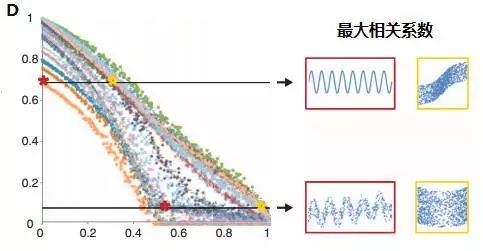
MIC与几种相关性评价算法的公平性对比见下图。图中横坐标代表噪声程度从0增长到1，纵坐标代表相关系数的大小，图中共有27种不同颜色的散点曲线代表不同的函数关系。从图A可以看出，随着噪声程度的增加，不同相关关系的MIC系数都是均匀降低，MIC可以为不同类型单噪声程度相似的相关关系给出相近的系数。图B-E分别是spearman系数、基于互信息的kraskov系数、最大相关系数、CorGC系数的公平性检测。可以看到，随着噪声程度的增加，这些方法对某些函数关系表现出的健壮性不一致。在大数据相关性挖掘中，数据难免会有噪声和异常点，如果没有良好的公平性，挖掘出的结果也就不再准确并且难以令人信服。利用MIC，可以大大减少数据清洗的麻烦，只要有足够的数据量可以代表总体信息，就可以直接用MIC计算分析。

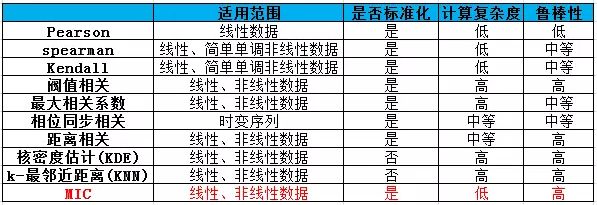
MIC算法与其它算法的优劣对比：

MIC的国内外应用

MIC通过对变量对(x,y)的散点图进行分割，利用动态规划的方式计算并搜索不同分割方式下所能达到的最大互信息值。最后，对最大互信息值进行标准化处理，所得结果即为MIC。MIC的范围为[0,1]，且具有对称性、良好的普适性和公平性。如果变量X与Y独立，则MIC(X,Y)=0；如果X与Y之间具有确定的关系，则MIC(X,Y)=1。作者在其著作中将MIC应用到了四个不同领域的高维数据集中：

（1）来自世界卫生组织(WHO)及其合作伙伴的社会、经济、卫生、政治领域上的数据(357个变量, 63546个变量对)。作者将MIC与互信息的结果进行了对比，发现互信息更善于捕获强线性相关关系，而对于MIC值较高的非线性关系，互信息给出的值较低。利用MIC，作者捕获到了一些有趣的关系模式，例如通过分析一个太平洋岛屿的数据得出女性体重与人均收入具有较强的相关关系，而通过世界总体数据却不能得出这个结果。通过深入调查发现，该岛屿上女性体重是地位的象征！！

（2）酵母菌基因表达谱(6223条基因)，此数据来自研究并展示基因表达水平与细胞周期变化关系的经典论文。这组数据集已经用Spearman方法分析过，主要用来确定在细胞周期内基因的转录震荡周期。MIC方法可以同时捕获高频震荡周期基因和低频震荡周期基因，而Spearman只能识别出其中20%的低频震荡周期基因。通过MIC，识别出了许多经典文献中已经发现的基因。

（3）自2008年起的美国职业棒球联盟(MLB)赛季表现统计。经MIC挖掘发现，与球员薪水具有强相关性的前三个因素分别为命中率、总基数和MLV，这一结论与之前传统的分析结论有所不同。利用MIC的结果，球队经理可以更好的选择球员和调整球队薪资。

（4）人体肠道菌落丰富度统计。人类肠道中生存着数以万亿记的细菌， 它们的遗传特性、分布特性等属性关系非常之复杂。MIC从22414860个关系中鉴定出了9472个显著的相关关系。分析前1001个系数值最高的非线性关系,研究者发现了许多意料之外的相关关系。如“不共存性”，一些菌落的丰富会导致另外几种菌落的减少；排名前500的大多数相关关系受宿主的几种特性或习惯的影响，如宿主饮食、性别、血型等。

国内自2013年开始，出现了MIC在不同领域应用的文献：蒋杭进将MIC应用到了脑网络分析中；为了有效的进行人脸特征选择，战泉茹利用MIC作为有效判据应用到了特征选择的单独最优特征组合法中；魏中强等人利用MIC与条件独立性测试，提出了一种新的贝叶斯网络结构学习算法（MICVO）；高凤将MIC应用到了股市关联度分析上，捕获到了上证综合指数与深证综合指数具有较强的相关关系（0.8141）。MIC作为一种有用的分析利器，正逐渐的被人们应用于不同的学科领域并正在走向实践！

MIC原理

在有足够的样本量时，MIC的公平性和通用性可以保证它能够捕获各种各样的有趣的关联，而不限于特定的函数类型。也就是说如果X与Y是相关的，它们必定存在这种关系:Y=f(X)，我们并不关注f的具体表达式是什么（事实上在大多数情况下，真正求出复杂关系的函数公式是相当困难的），只要X与Y存在f这种映射关系，都有M(X,Y)=1。MIC是基于互信息的，实际上MIC(X,Y)就是Y中能被X解释的信息量的百分比。在理想化的情况下，如果两个变量相互独立，则它们的MIC应该为0。

对于一个有序对的有限集合D，我们可以将D的第一个变量分割成x段，将D的第二个变量分割成y段。我们将这种分割方式称为x乘y分辨率的网格分割。给定一个x乘y的网格G，令表示集合D中的点落在网格G上的概率分布。通过调整x乘y网格的分割方式,可以得到不同的概率分布。

对于一个有限集合

和正整数x与y，定义：

公式中的含义是，对于x乘y分辨率的网格分割，通过调整X轴和Y轴的分割点所能计算得到的最大互信息值。有了在不同分辨率下得到的，我们就可以构造特征矩阵并求得有限集合D的特征矩阵。

定义二维集合D的特征矩阵M(D)是一个无穷矩阵：

经过标准化后的特征矩阵中元素的值均落在[0,1]上。对于标准化的合理性证明，假设网格进行了x乘y分辨率的划分，对有限集合D的第一个变量分割得到的x个格子分别为 

, 对第二个变量分割得到的y个格子分别为 

以二维散点图的角度看，可令表示点落在第i列的概率，表示点落在第j行的概率，而表示点落在第i列第j行的概率。可得：

于是有：

综上，

同理也有

于是

.从而证得

设二维有限集合D的长度为n,则集合D的最大信息系数(MIC)定义为：

其中，网格规模需小于B(n), 

对任意的

成立。

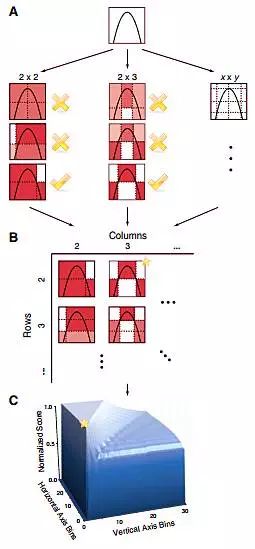
直观的说，MIC是基于这样的思想：如果两个变量之间存在着一种关系，则可以将两个变量组成有限集合D，在集合D的散点图中绘制网格，这些网格可以将散点图中的数据分割。这样有些网格是空的有些则含有散点图中的点，根据点在网格中的分布，可以得到这种分割方式下的概率分布，通过概率分布进行熵和互信息的计算。逐步增大网格的分辨率(比如由2乘2增大到x乘y)，在每种分辨率下改变分割点的位置，可以搜索计算得到这种分辨率下的最大互信息值。标准化这些互信息值，以确保不同分辨率的网格之间进行公平的比较。

定义矩阵

其中是在每种分辨率下计算得到的最大互信息标准化值，而MIC就是M中的最大值。MIC计算过程示意图如下：

为了计算M，理论上应该对所有可能的分辨率下的所有网格分割方式进行计算，但是当n很大时，计算量会非常的大。有一种近似计算的方式，即将每种分辨率下纵坐标轴均进行等距离分割，计算出MIC后将a和b交换坐标轴重新计算MIC，取两次计算的最大值为最终的MIC值。令P为x分辨率下的横坐标轴的某种分割方式，令Q为y分辨率下的纵坐标轴的等距离分割方式。令的值为散点图落在P中第i列中的点数，的值为散点图落在Q中第j行中的点数，的值为散点图落在第i列第j行的格子中的点数。于是有： 

而互信息I(P;Q)=H(P)+H(Q)-H(P;Q)。

MIC具有以下优良的性质：

（1）MIC是标准化后的互信息值，取值范围为[0,1]；

（2）由于MIC是基于互信息的，所以也具有互信息的对称性质：

（3）若X与Y具有相关关系，则MIC(X,Y)=1；反之MIC(X,Y)=0；

（4）MIC具有良好的稳健性。若X与Y的数据含有噪声，如果X与Y具有相关关系，随着样本量的增加MIC(X,Y)仍然收敛到1；反之MIC(X,Y)仍然收敛到0。

---

---

---

https://blog.csdn.net/allein_STR/article/details/121458868