为什么贝叶斯统计如此重要?
↑↑↑关注后"星标"Datawhale
每日干货 & 每月组队学习,不错过
Datawhale干货
译者:张峰,Datawhale成员
即使对于一个非数据科学家来说,贝叶斯统计这个术语也已经很流行了。你可能在大学期间把它作为必修课之一来学习,而没有意识到贝叶斯统计有多么重要。事实上,贝叶斯统计不仅仅是一种特定的方法,甚至是一类方法;它是一种完全不同的统计分析范式。

为什么贝叶斯统计如此重要
贝叶斯统计为你提供了在新数据的证据中更新你的评估工具,这是一个在许多现实世界场景中常见的概念,如跟踪大流行病,预测经济趋势,或预测气候变化。贝叶斯统计是许多较著名的统计模型的支柱,如高斯过程。
重要的是,学习贝叶斯统计原理可以成为你作为一个数据科学家的宝贵财富,因为它给你一个全新的视角来解决具有真实世界动态数据来源的新问题。
这篇文章将介绍贝叶斯统计的基本理论,以及如何在Python中实现一个简单的贝叶斯模型。
目录表:
01 什么是贝叶斯统计?
02 贝叶斯编程简介
03 贝叶斯的工作流程
04 建立一个简单的贝叶斯模型
闲话少说,进入主题!让我们开始介绍贝叶斯统计编程。
01 什么是贝叶斯统计?
你可能会在互联网上的某个地方或在你的课堂上看到这个方程式。
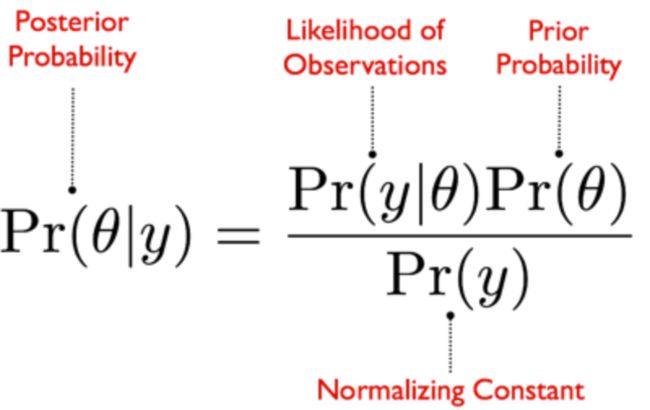
如果你没有,也不要担心,因为我将向你简要介绍贝叶斯的基本原则以及该公式的工作原理。
关键术语
上述贝叶斯公式的组成部分一般被称为概率声明。例如,在下面的后验概率声明中,该术语的意思是 "给定观测值y,theta(θ)的概率是多少 "。
Theta(θ)是这里的未知数,被称为我们所关心的参数。参数的不确定性遵循一个特定的概率分布,可以使用与数据相关的模型组合来估计有关参数。
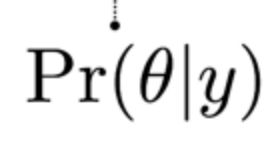
上述贝叶斯统计表述也被称为反概率,因为它是从观察到参数开始的。换言之,贝叶斯统计试图从数据(效果)中推断出假设(原因),而不是用数据来接受/拒绝工作假设。
贝叶斯公式
那么,贝叶斯公式告诉我们什么呢?
后验概率是我们想知道的主要部分,因为Theta(θ)是我们感兴趣的参数。
观察的可能性仅仅意味着,在Theta(θ)的特定值下,数据y在现实世界中出现的可能性有多大。
先验概率是我们对Theta (θ)应该是什么样子的最佳猜测(例如,也许它遵循正态或高斯分布)。
归一化常数只是一个系数常数,使整个方程积分为1(因为概率不能低于0和高于1)。
现在我们已经涵盖了贝叶斯统计的基本理论,让我们开始为即将到来的贝叶斯编程教程进行设置。
02 贝叶斯编程介绍
安装
首先,安装PyMC3作为我们执行贝叶斯统计编程的首选库。
推荐使用conda
conda install -c conda-forge pymc3
也可使用pip
pip install pymc3
获取数据
我们将使用描述美国家庭中氡气(Radon)浓度的氡气数据集。氡气已被证明是非吸烟者患肺癌的最高预测因素之一,其浓度通常与房屋的整体条件(例如,是否有地下室,等等)有关。
首先,在你的笔记本或终端运行以下命令:
!wget "https://raw.githubusercontent.com/fonnesbeck/mcmc_pydata_london_2019/master/data/radon.csv"
确保你的数据位于你的笔记本的同一目录内。
数据探索
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
import numpy as npradon = pd.read_csv('./radon.csv', index_col=0)radon.head()
我们注意到,有29列描述了一个家庭中氡(Radon)的浓度。
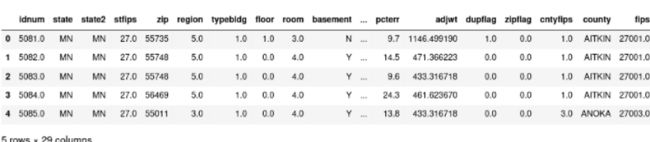 数据集汇总
数据集汇总
让我们画一张图,显示 "ANOKA "的氡的对数浓度分布,用一条垂直线来说明对数浓度为1.1。
anoka_radon = radon.query('county=="ANOKA"').log_radon
sns.distplot(anoka_radon, bins=16)plt.axvline(1.1)
 密度分布
密度分布
ANOKA地区氡气对数浓度超过1.1的家庭比例似乎相当大,这是一个令人担忧的趋势......
03 贝叶斯工作流
现在我们有了数据,让我们进行贝叶斯推断。一般来说,这个过程可以分解为以下三个步骤。
第1步:指定一个概率模型
这是作为建模者要多做选择的地方。你将需要为一切指定最可能的概率分布函数(例如,正态或高斯、考奇、二项式、t分布、F分布,等等)。
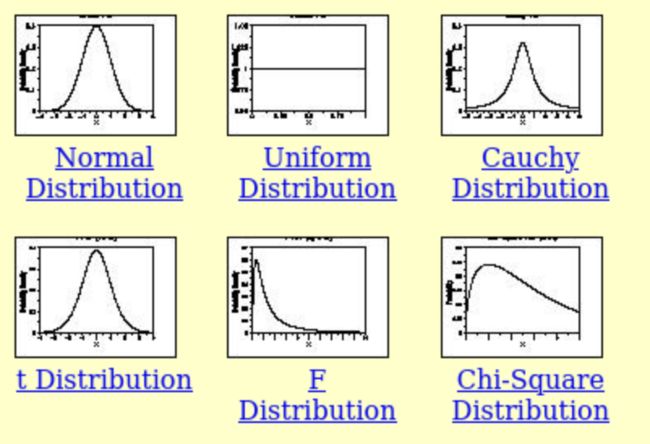
我所说的一切,是指包括未知参数、数据、协变量、缺失数据、预测在内的一切。所以,用不同的分布函数做实验,看看在现实世界的场景中如何起效。
第2步:计算后验分布
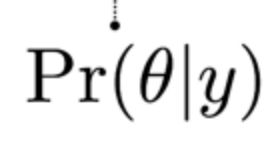
现在你将计算这个概率项,给定贝叶斯方程右边的所有项。
第3步:检查你的模型
与其他ML模型一样,评估你的模型是关键。回到第一步,检查你的假设是否有意义。如果没有,改变概率分布函数,并反复重申。
04 建立一个简单的贝叶斯模型
现在,我将向你介绍一个简单的编程练习来建立你的第一个贝叶斯模型。
第1步:定义一个贝叶斯模型
首先,让我们定义我们的氡气——贝叶斯模型,有两个参数,平均值(μ-"miu")和其偏差(σ-"sigma")。这些参数(μ和σ)还需要通过选择对应的分布函数来建立模型(记住:我们必须为所有参数定义概率分布)。
对于这些,我们选择的函数是正态/高斯分布(μ=0,σ=10)和均匀分布。你可以在模型的验证检查中重新校准这些值,如上面步骤3所述。
from pymc3 import Model, Normal, Uniformwith Model() as radon_model:
μ = Normal(’μ’, mu=0, sd=10)
σ = Uniform(’σ’, 0, 10)
下一步是用另一个概率分布来编译radon_model本身。
**with** radon_model:
dist = Normal('dist', mu=μ, sd=σ, observed=anoka_radon)
第2步:用数据进行模型拟合
现在,我们需要用数据来拟合这个模型(即训练)。
from pymc3 import sample
**with** radon_model:
samples = sample(1000, tune=1000, cores=2, random_seed=12)
让我们画出我们的参数μ在训练后的分布情况,同时画出95%的置信线。
from arviz import plot_posterior
plot_posterior(samples, var_names=['μ'], ref_val=1.1)

好吧,看来1.1的对数浓度可能不是那么糟糕,因为它是在分布的尾端(只有2.2%的样品的对数浓度大于1.1)。
来源:https://towardsdatascience.com/bayesian-statistical-programming-an-introduction-4ca3e2ddae76
整理不易,点赞三连↓
