学校课后习题
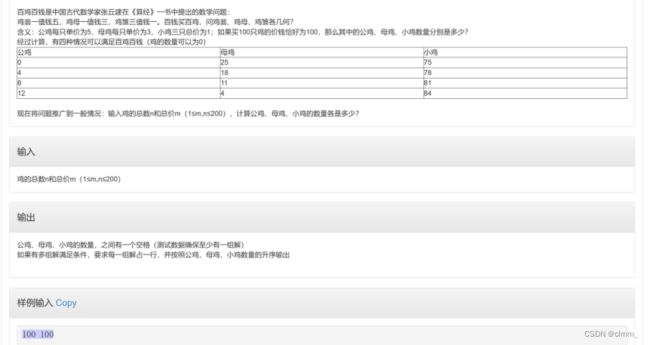
【程序1】百鸡百钱
穷举法遍历所有情况,变量有三个,所以写一个简单的三重循环
#include
int main()
{
int n = 0;
int m = 0;
scanf("%d%d", &n, &m);
int fa, mo, c;
for (fa = 0; fa <= n; fa++)
{
for (mo = 0; mo <= n; mo++)
{
for (c = 0; c <= n; c+=3)
{
if (fa + mo + c == n && 5 * fa + 3 * mo + c / 3 == m)
{
printf("%d %d %d\n", fa, mo, c);
}
}
}
}
return 0;
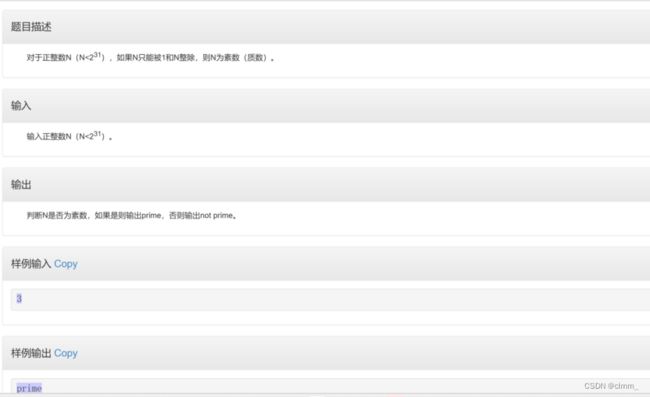
} 【程序2】判断一个数是否为素数
注意:
1.数字1不是素数
2.一个数最大的约数不能大于其根号,所以遍历的时候 i <= sqrt(n)
#include
int main()
{
int n = 0;
scanf("%d", &n);
int i = 0;
int m = sqrt(n);
if (n == 1)
{
printf("not prime");
return 0;
}
for (i = 2; i <= m; i++)
{
if (n % i == 0)
{
printf("not prime");
return 0;
}
}
printf("prime");
return 0;
} 【程序3】将N3分解为连续奇数和
观察到,输入n,便有n个奇数相加,且奇数是递增的等差数列,d = 2
#include
int main()
{
int n = 0;
scanf("%d", &n);
int m = n * n * n;
int i = 0;
int j = 0;
int sum = 0;
for (i = 1; i <= m; i += 2)
{
int temp = i;
for (j = 0; j < n; j++)
{
sum += temp;
temp += 2;
}
if (sum == m)
{
printf("%d^3=", n);
temp = i;
for (j = 0; j < n; j++)
{
if (j == n - 1)
{
printf("%d", temp);
}
else
{
printf("%d+", temp);
}
temp += 2;
}
break;
}
sum = 0;
}
return 0;
} 【程序4】将N分解为素数因子的连乘式
#include
int main()
{
int n = 0;
scanf("%d", &n);
int m = n;
int i = 2;
int count = 0;
for (i = 2; i < m; i++)
{
if (n % i == 0)
{
n /= i;
if (n == 1)
{
printf("%d", i);
}
else
{
printf("%d*", i);
}
i = 1;//因为再进行循环时会被++,
//所以如果写i = 2,那就会变成3,
//后面就考虑不到i = 2的情况
count++;
}
}
if (count == 0)
{
printf("%d", n);
}
return 0;
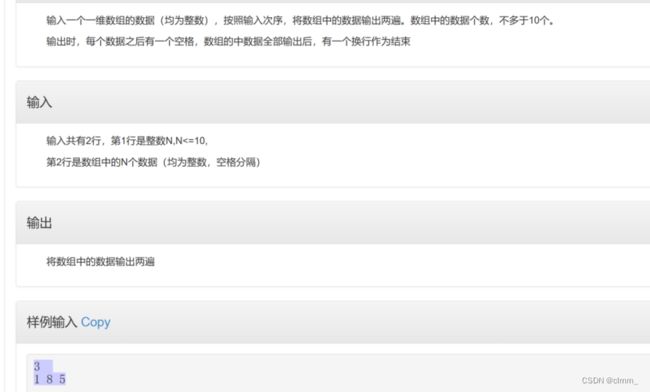
} 【程序5】输出数组中的数据
#include
int main()
{
int n = 0;
scanf("%d", &n);
int i = 0;
int a[10] = { 0 };
int input = 0;
for (i = 0; i < n; i++)
{
scanf("%d", &input);
a[i] = input;
}
for (i = 0; i < n; i++)
{
printf("%d ", a[i]);
}
printf("\n");
for (i = 0; i < n; i++)
{
printf("%d ", a[i]);
}
printf("\n");
return 0;
} 这题简单,但要知道scanf的特性
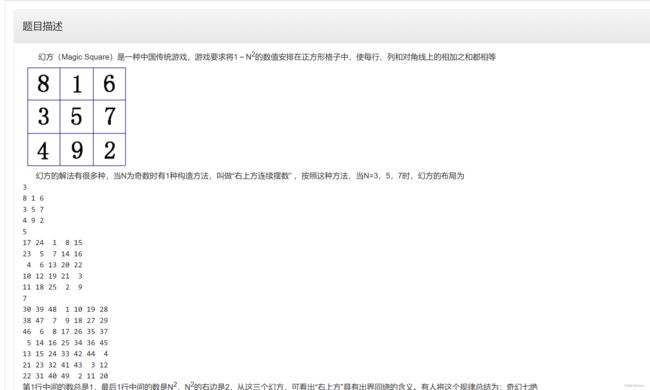
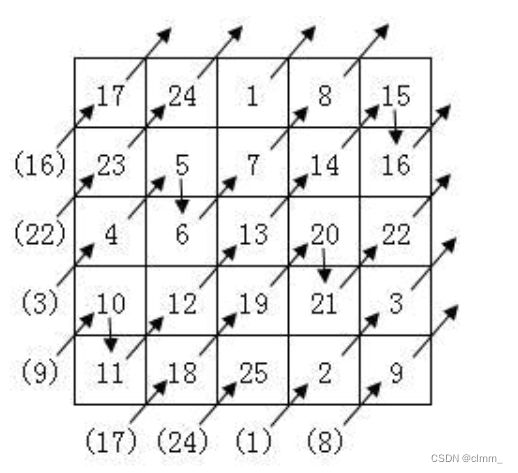
【程序6】奇数阶幻方
#include
int main()
{
int n = 0;
scanf("%d",&n);
int arr[20][20] = {0};
int row = 0,col = (n-1)/2;
arr[row][col] = 1;//填1
int count = 0;
int temp = 0;
while(count=n)//从右上角出 ,看作重复
{
temp = arr[row][col];
row+=1;
arr[row][col] = temp+1;
}
else if(col+1>=n)//从右边出
{
temp = arr[row][col];
col = -1;
col+=1;
row-=1;
arr[row][col] = temp+1;
}
else if(row-1<0)//从上边出
{
temp = arr[row][col];
row = n;
row-=1;
col+=1;
arr[row][col] = temp+1;
}
else if(arr[row-1][col+1]!=0)//重复,该格子已有数字 ,注意!这一步必须放在判断是否出界之后
{
temp = arr[row][col];
row+=1;
arr[row][col] = temp+1;
}
else//不出界,不重复
{
temp = arr[row][col];
row-=1;
col+=1;
arr[row][col] = temp+1;
}
}
int i,j;
for(i = n-1;i>=0;i--)//列
{
for(j = n-1;j>=0;j--)//行
{
printf("%4d",arr[j][i]);
}
printf("\n");
}
return 0;
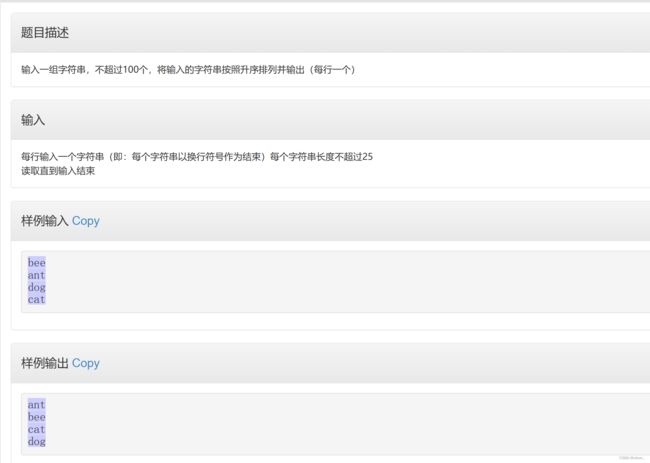
} 【程序7】排序字符串长度
注意!
输入:ant,az。输出:ant,az。因为比较首字母,都一样是a,所以继续比较下一个字母,z>n,所以字符串ant比字符串az小
输入:azt,az。输出:az,azt。因为前面都一样的情况下,azt比az多一个字符,所以字符串az比字符串azt小
#include
#include
void BubbleSort(char arr[][26], int n)
{
int i, j;
char* temp = (char*)malloc(100);
if (temp == NULL)
{
exit(0);
}
for (i = 0; i < n - 1; i++)
{
for (j = 0; j < n - i - 1; j++)
{
if (strcmp(arr[j], arr[j + 1]) > 0)//注意,这里要用strcpm,因为就算当首字母相同的情况下,也要逐个比较后面字符的大小
{
strcpy(temp, arr[j]);
strcpy(arr[j], arr[j + 1]);
strcpy(arr[j + 1], temp);
}
}
}
free(temp);
temp = NULL;
}
int main()
{
char arr[101][26] = { 0 };
int i = 0, j = 0;
int count = 0;
while (count <= 100 && scanf("%s", arr[count]) != EOF)
{
count++;
}
BubbleSort(arr, count);
for (i = 0; i < count; i++)
{
puts(arr[i]);
}
return 0;
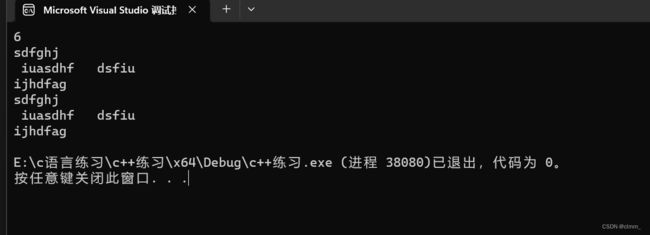
} 【程序8】gets函数的使用
gets函数可以输入空格,而scanf遇到空格就不输入了
注意!只有输入或输出字符串的时候才用gets和puts!
函数原型如下
gets函数使用注意事项
在连续使用 gets() 函数时,可能会遇到读取上一行输入留下来的回车符(\n)的问题,导致后续的输入被跳过。这是因为 gets() 函数会读取输入流中的换行符,并将其放入输入字符串中。当程序再次调用 gets() 函数时,它会立即读取上一次输入剩余的回车符,然后返回一个空字符串。
错误使用1:因为输入整数n后,后面的gets函数会读取上一次输入的回车键换行符,所以第一次gets(name[i])会跳过输入,因为读取到了 '\n'。
int main() {
char name[101][31] = { 0 };
int i = 0;
int n = 0;
scanf_s("%d", &n);
//getchar();
for (i = 0; i < 3; i++) {
gets_s(name[i]);
}
for (i = 0; i < 3; i++) {
puts(name[i]);
}
return 0;
}错误使用2:输入字符后,后面循环里再用gets函数,也会出现跟错误1中同样的问题
int main() {
char name[101][31] = { 0 };
int i = 0;
char n = 0;
scanf_s("%c", &n);
//getchar();
for (i = 0; i < 3; i++) {
gets_s(name[i]);
}
for (i = 0; i < 3; i++) {
puts(name[i]);
}
return 0;
}以上错误都是因为在输入字符串前,输入了字符或整形,所以输入字符串的时候会读取到 '\n',但如果都是输入字符串,就没问题
int main() {
char name[101][31] = { 0 };
int i = 0;
char arr[10] = { 0 };
gets_s(arr);
for (i = 0; i < 3; i++) {
gets_s(name[i]);
}
for (i = 0; i < 3; i++) {
puts(name[i]);
}
return 0;
}那如果一定要用gets输入字符串,而且在这之前还要输入别的类型(如:整形,字符),怎么解决?
正确使用:加上getchar,去掉上一次输入的换行符
int main() {
char name[101][31] = { 0 };
int i = 0;
int n = 0;
scanf_s("%d", &n);
getchar();
for (i = 0; i < 3; i++) {
gets_s(name[i]);
}
for (i = 0; i < 3; i++) {
puts(name[i]);
}
return 0;
}【程序9】辗转相除法
int gcd(int a,int b)
{
int r;
while(b!=0){
r=a%b;
a=b;
b=r;
}
return a;
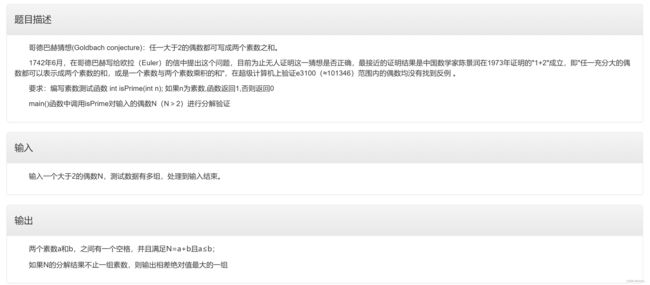
}【程序10】使用素数测试函数验证哥德巴赫猜想
超时代码
int IsPrime(int x) {
if (x == 1) {
return 0;
}
int i = 0;
for (i = 2; i <= x/2; i++) {
if (x % i == 0) {
return 0;
}
}
return 1;
}
void FindPrime(int n) {
int i, j;
int a = 0, b = 0;
int d = -1;
for (i = 2; i < n; i++) {
if (IsPrime(i) && IsPrime(n - i)) {
if (d < fabs(a - b)) {
a = i, b = n - i;
d = abs(a - b);
}
//这里其实没必要判断相差绝对值最大,
//因为i从2开始遍历,第一个符合条件的已经是相差绝对值最大的情况
}
}
printf("%d %d\n", a, b);
}
int main()
{
int input = 0;
while (scanf("%d", &input) != EOF) {
FindPrime(input);
}
return 0;
}优化后
int isPrime(int a)
{
for(int i=2;i<=a/2;i++){
if(a%i==0){
return 0;
}
}
return 1;
}
#include
int main()
{
int n;
while(~(scanf("%d",&n))){
if(n==4){
printf("2 2\n");
}
else{
for(int a=2;a<=n/2;a++){
if(isPrime(a)&&isPrime(n-a)){
printf("%d %d\n",a,n-a);
break;//一旦找到,及时跳出,提高时间效率
}
}
}
}
return 0;
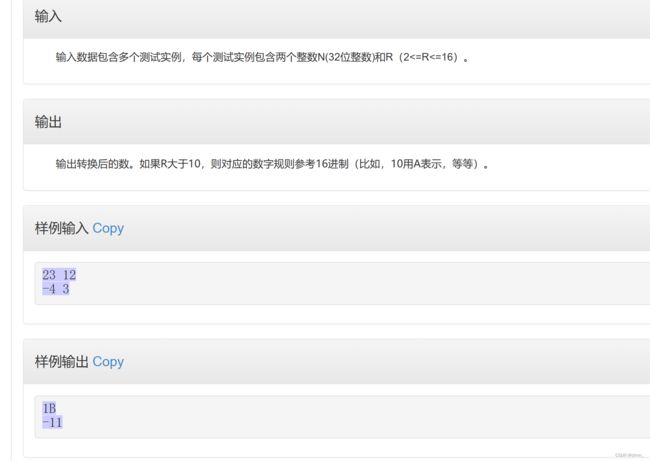
} 【程序11】十进制转换成R进制
十进制转换成二进制
void decToBin(int n) {
int arr[35] = {0};
if(n==0){
printf("0");
return;
}
if(n<0){
printf("-");
n = -n;
}
int i = 0;
while(n){
arr[i] = n%2;
n/=2;
i++;
}
i-=1;
while(i>=0){
printf("%d",arr[i]);
i--;
}
}十进制转换成R进制
void decToR(int n,int r) {
char arr[35] = {0};
if(n==0){
printf("0");
return;
}
if(n<0){
printf("-");
n = -n;
}
int i = 0;
while(n){
if(n%r>=10){
arr[i] = n%r-10+'A';
}
else{
arr[i] = n%r+'0';
}
n/=r;
i++;
}
i-=1;
while(i>=0){
printf("%c",arr[i]);
i--;
}
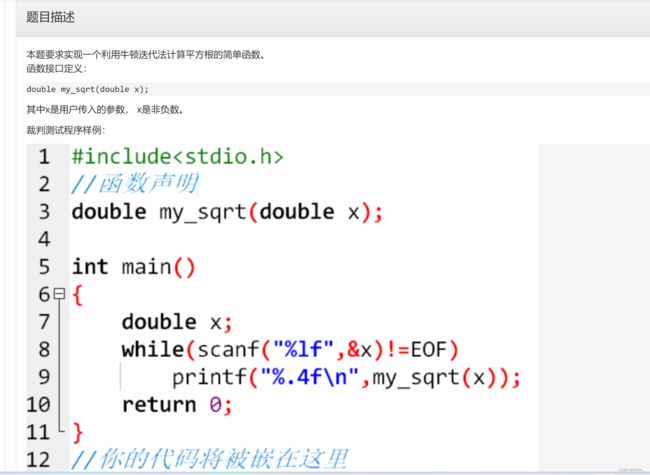
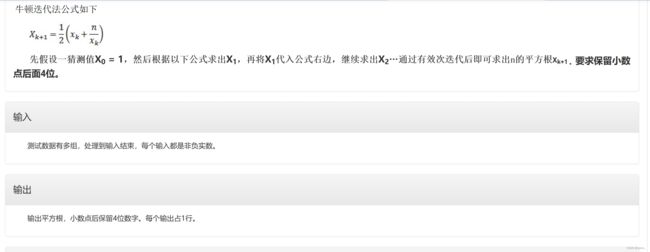
}【程序12】自定义平方根函数my_sqrt
double my_sqrt(double n)
{
double x1=1;
for(;;){
double x2=(x1+n/x1)/2;
if(x2>x1&& x2-x1 <1e-5){
return x2;
}
if(x1>x2&&x1-x2<1e-5){
return x2;
}
x1=x2;
}
}【程序13】四边形的面积
要用到海伦公式,已知三角形的三条边,求其面积
#include
struct Node{
double x;
double y;
}p_node[4],node[4];
int main()
{
int i = 0;
for(i = 0;i < 4;i++){
scanf("%lf%lf",&p_node[i].x,&p_node[i].y);
}
//点A
node[0].x = (p_node[0].x+p_node[1].x)/2;
node[0].y = (p_node[0].y+p_node[1].y)/2;
//点B
node[1].x = (p_node[1].x+p_node[2].x)/2;
node[1].y = (p_node[1].y+p_node[2].y)/2;
//点C
node[2].x = (p_node[2].x+p_node[3].x)/2;
node[2].y = (p_node[2].y+p_node[3].y)/2;
//点D
node[3].x = (p_node[0].x+p_node[3].x)/2;
node[3].y = (p_node[0].y+p_node[3].y)/2;
double AC = sqrt((node[0].x-node[2].x)*(node[0].x-node[2].x)+(node[0].y-node[2].y)*(node[0].y-node[2].y));
double AB = sqrt((node[0].x-node[1].x)*(node[0].x-node[1].x)+(node[0].y-node[1].y)*(node[0].y-node[1].y));
double BC = sqrt((node[1].x-node[2].x)*(node[1].x-node[2].x)+(node[1].y-node[2].y)*(node[1].y-node[2].y));
double s = (AB+BC+AC)/2;
double S = sqrt(s*(s-AB)*(s-BC)*(s-AC));
printf("%.2f",S*2);
return 0;
} 【程序14】十进制转二进制(递归版)
正确代码
void decToBin(int n){
if(n<0){
n = -n;
printf("-");
}
//这一步要注意,当n小于二进制的2
//直接打印并返回
if (n < 2) {
printf("%d",n);
return;
}
decToBin(n/2);
printf("%d",n%2);
}错误代码1
看似没问题,但忽略了 n==0 时也要打印0
void decToBin(int n){
if(n<0){
n = -n;
printf("-");
}
if (n == 0) {
return;
}
decToBin(n/2);
printf("%d",n%2);
}错误代码2
修改后
void decToBin(int n){
if(n==0){
printf("0");//解决了n==0时要打印0的问题
return;
}
if(n<0){
n = -n;
printf("-");
}
decToBin(n/2);
printf("%d",n%2);
}但还是有错误,因为深度优先遍历到底层,到最底层的n==0时,不用打印0。
反正就是很难考虑
【程序15】十进制转R进制(递归版)
void decToR(int x,int r) {
if(x<0){
x = -x;
printf("-");
}
if(r==10){
printf("%d",x);
return;
}
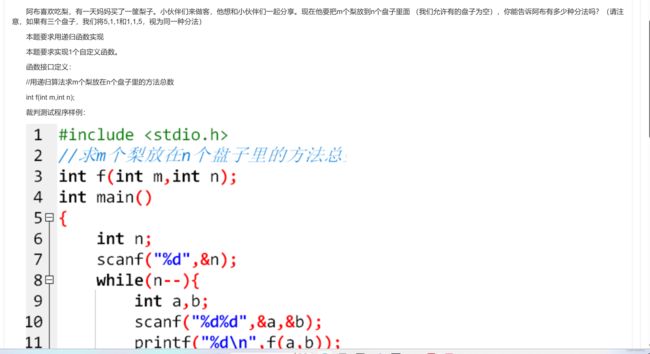
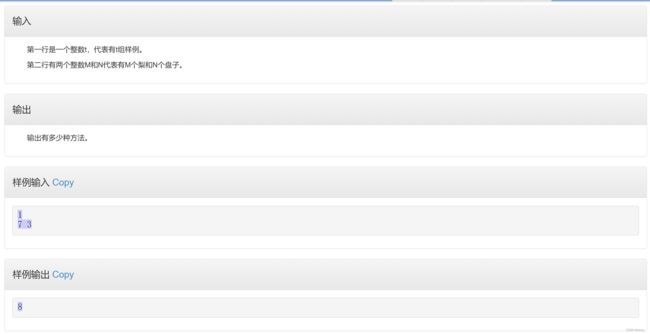
if(x【程序16】分梨
题解要点:
1、如果盘子数为0,那么无论多少个梨,方法都为1(包括0个梨)
2、如果梨的数量为0,那么无论多少个盘子,方法都为1(包括0个盘子)
3、如果盘子和梨的数量都不为0,那么有两种情况
(1)梨的数目(m)大于盘子的数目(n),那么方法数f[m][n]应该是f[m-n][n]+f[m][n-1],即每一个盘子都有梨,那么方法数应该是梨-盘子(假设每一个盘子都放入一个梨,那么前式就是所剩下的梨),将他们放入n个盘子中,这是第一种可能,第二种可能就是至少有一个盘子为空,即f[m][n-1]
(2)如果梨的数目(m)小于盘子的数目(n),那么方法数就是将m个梨放在m个盘子里面,这点题目没提示,要能想得到
//m是梨,n是盘子
int f(int m,int n){
if(m==1){
return 1;
}
if(m<=0){
return 1;
}
if(n==1){
return 1;
}
if(n<=0){
return 0;
}
if(m小结:递归算法,就是要考虑到特殊情况,正如题解要点1和2。
但是,有时候也要根据具体题目进行分类讨论,例如这题里,要分类讨论m和n之间的大小关系
【程序17】计算组合数
这题简单,看着提示做就行了
int comb(int m,int n){
if(n==0){
return 1;
}
if(m==n){
return 1;
}
return comb(m-1,n-1)+comb(m-1,n);
}【程序18】汉诺塔
//移动盘子和打印移动盘子的路径
void move_Print(char a,char c,int n){
printf("move %d# from %c to %c\n",n,a,c);
}
//A是起始柱,B是中转柱,C是终点柱
//这个函数充当移动盘子的功能
void Hanoi(int n,char a,char b,char c){
if(n==1){
move_Print(a,c,n);
//只有一个盘子,那直接从A移到C就好
return;
}
//当n大于1时,情况就比较具有普适性了,
//因为三个柱子都有用到
Hanoi(n-1,a,c,b);
//把除了底盘的n-1个盘子移动到 中转柱B
move_Print(a,c,n);
//把底盘移动到终点柱C
Hanoi(n-1,b,a,c);
//再把刚刚的n-1个盘子移动到终点柱C
}
int main(){
int n;
scanf("%d",&n);
Hanoi(n,'A','B','C');
return 0;
}【程序19】求组合数(高效递归版)
double Cmb(int x, int y)
{
if(x==0||y==0||x==y){
return 1;
}
if(x<0||y<0||y>x){
return 0;
}
//以上的特殊情况要考虑周全
//减少计算量
if(y>x/2){
y = x-y;
}
return Cmb(x-1,y-1)*x/y;//利用公式
}这样也行,不过以防万一还是按上面那样完整一点地写
double Cmb(int x, int y)
{
if (x == 0 || y == 0 || x == y) {
return 1;
}
if (y > x / 2) {
y = x - y;
}
return Cmb(x - 1, y - 1) * x / y;
}【程序20】打印菱形
#include
#include
#include
#include
int main(){
int n;
scanf("%d",&n);
int i,j;
for(i = 1;i<=n;i++){
for(j = 0;j=1;i--){
for(j = 0;j