遗传算法解决TSP问题
遗传算法解决TSP问题
- 一、遗传算法与TSP问题
-
- 1.1 TSP问题回顾
- 1.2 遗传算法描述
- 1.3 算法实现步骤
- 1.4 算法流程图
- 二、代码与解释
- 三、结果与分析
-
- 3.1 种群规模对算法性能的影响
- 3.2 城市序列对算法性能的影响
- 3.3 城市个数对算法性能的影响
- 3.4 交叉概率对算法性能的影响
- 3.5 变异概率对算法性能的影响
- 四、小结(注意点)
一、遗传算法与TSP问题
1.1 TSP问题回顾
TSP问题,即旅行商问题,是数学领域中著名问题之一。假设有一个旅行商人要拜访n个城市,他必须选择所要走的路径,路径的限制是每个城市只能拜访一次,而且最后要回到原来出发的城市。路径的选择目标是要求得的路径路程为所有路径之中的最小值。
1.2 遗传算法描述
遗传算法是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型,通过模拟自然进化过程搜索最优解。
遗传算法是从代表问题可能潜在的解集的一个种群开始的,初代种群产生之后,按照适者生存和优胜劣汰的原理,逐代演化产生出越来越好的近似解,在每一代,根据问题域中个体的适应度大小选择个体,并借助于自然遗传学的遗传算子进行组合交叉和变异,产生出代表新的解集的种群。这个过程将导致种群像自然进化一样的后生代种群比前代更加适应于环境,末代种群中的最优个体经过解码,可以作为问题近似最优解。
应用遗传算法解决 TSP 问题,首先对访问城市序列进行排列组合的方法编码,这保证了每个城市经过且只经过一次。接着生成初始种群,并计算适应度函数,即计算遍历所有城市的距离。然后用最优保存法确定选择算子,以保证优秀个体直接复制到下一代。采用有序交叉和倒置变异法确定交叉算子和变异算子。
1.3 算法实现步骤
1.初始化阶段
初始化对象:种群规模、城市数量、运行代数、交叉概率、变异概率
初始化数据:读入数据源,将坐标转换为距离矩阵(标准化欧式距离)
初始化种群:随机生成M个路径序列,M表示种群规模
2.计算种群适应度
已知任意两个城市之间的距离,每个染色体可计算出总距离,因此可以将一个随机全排列的总距离的倒数作为适应度函数,即距离越短,适应度函数越好。
3.计算累计概率
计算初始化种群中各个个体的累积概率。
4.迭代
选择算子:赌轮选择策略挑选下一代个体。
交叉运算:在交叉概率的控制下,对群体中的个体两两进行交叉。
变异运算:在变异概率的控制下,对群体中的个体两两进行变异,即对某一个体的基因进行随机调整。
计算新的种群适应度以及个体累积概率,并更新最优解。
将新种群复制到旧种群中,准备下一代进化(迭代)。
5.输出
输出迭代过程中产生的最短路径长度以及最短路径。
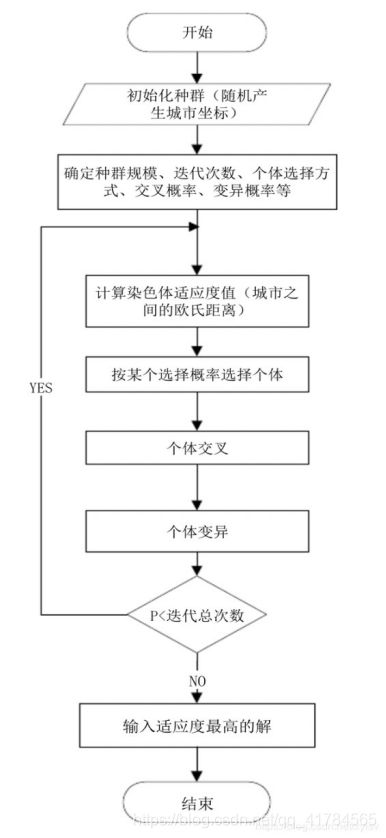
1.4 算法流程图
二、代码与解释
plot_route.m
——连点画图函数
function plot_route(a,R)
scatter(a(:,1),a(:,2),'rx');
hold on;
plot([a(R(1),1),a(R(length(R)),1)],[a(R(1),2),a(R(length(R)),2)]);
hold on;
for i=2:length(R)
x0=a(R(i-1),1);
y0=a(R(i-1),2);
x1=a(R(i),1);
y1=a(R(i),2);
xx=[x0,x1];
yy=[y0,y1];
plot(xx,yy);
hold on;
end
end
mylength.m
——染色体的路程代价函数 :用于计算每个染色体对应的总长度
function len=myLength(D,p)%p是一个排列
[N,NN]=size(D);
len=D(p(1,N),p(1,1));
for i=1:(N-1)
len=len+D(p(1,i),p(1,i+1));
end
end
fit.m
——适应度函数:每次迭代都要计算每个染色体在本种群内部的优先级别,类似归一化参数。越大越好!
function fitness=fit(len,m,maxlen,minlen)
fitness=len;
for i=1:length(len)
fitness(i,1)=(1-(len(i,1)-minlen)/(maxlen-minlen+0.0001)).^m;
end
Mutation.m
——变异函数
function a=Mutation(A)
index1=0;index2=0;
nnper=randperm(size(A,2));
index1=nnper(1);
index2=nnper(2);
%fprintf('index1=%d ',index1);
%fprintf('index2=%d ',index2);
temp=0;
temp=A(index1);
A(index1)=A(index2);
A(index2)=temp;
a=A;
end
exchange.m
——对调函数
function [x,y]=exchange(x,y)
temp=x;
x=y;
y=temp;
end
cross.m
——交叉操作函数
function [A,B]=cross(A,B)
L=length(A);
if L<10
W=L;
elseif ((L/10)-floor(L/10))>=rand&&L>10
W=ceil(L/10)+8;
else
W=floor(L/10)+8;
end
%%W为需要交叉的位数
p=unidrnd(L-W+1);%随机产生一个交叉位置
%fprintf('p=%d ',p);%交叉位置
for i=1:W
x=find(A==B(1,p+i-1));
y=find(B==A(1,p+i-1));
[A(1,p+i-1),B(1,p+i-1)]=exchange(A(1,p+i-1),B(1,p+i-1));
[A(1,x),B(1,y)]=exchange(A(1,x),B(1,y));
end
end
mian.m
——主程序
%main
clear;
clc;
%%%%%%%%%%%%%%%输入参数%%%%%%%%
N=25; %%城市的个数
M=100; %%种群的个数
ITER=2000; %%迭代次数
%C_old=C;
m=2; %%适应值归一化淘汰加速指数
Pc=0.8; %%交叉概率
Pmutation=0.05; %%变异概率
%%生成城市的坐标
pos=randn(N,2);
%%生成城市之间距离矩阵
D=zeros(N,N);
for i=1:N
for j=i+1:N
dis=(pos(i,1)-pos(j,1)).^2+(pos(i,2)-pos(j,2)).^2;
D(i,j)=dis^(0.5);
D(j,i)=D(i,j);
end
end
%%生成初始群体
popm=zeros(M,N);
for i=1:M
popm(i,:)=randperm(N);%随机排列,比如[2 4 5 6 1 3]
end
%%随机选择一个种群
R=popm(1,:);
%figure(1);
subplot(2,2,1);
scatter(pos(:,1),pos(:,2),'rx');%画出所有城市坐标
axis([-3 3 -3 3]);
title('图a');
%figure(2);
subplot(2,2,2);
plot_route(pos,R); %%画出初始种群对应各城市之间的连线
axis([-3 3 -3 3]);
title('图b');
%%初始化种群及其适应函数
fitness=zeros(M,1);
len=zeros(M,1);
for i=1:M%计算每个染色体对应的总长度
len(i,1)=myLength(D,popm(i,:));
end
maxlen=max(len);%最大回路
minlen=min(len);%最小回路
fitness=fit(len,m,maxlen,minlen);
rr=find(len==minlen);%找到最小值的下标,赋值为rr
R=popm(rr(1,1),:);%提取该染色体,赋值为R
for i=1:N
fprintf('%d ',R(i));%把R顺序打印出来
end
fprintf('\n');
fitness=fitness/sum(fitness);
distance_min=zeros(ITER+1,1); %%各次迭代的最小的种群的路径总长
nn=M;
iter=0;
while iter<=ITER
fprintf('迭代第%d次\n',iter);
%%选择操作
p=fitness./sum(fitness);
q=cumsum(p);%累加
for i=1:(M-1)
len_1(i,1)=myLength(D,popm(i,:));
r=rand;
tmp=find(r<=q);
popm_sel(i,:)=popm(tmp(1),:);
end
[fmax,indmax]=max(fitness);%求当代最佳个体
popm_sel(M,:)=popm(indmax,:);
%%交叉操作
nnper=randperm(M);
% A=popm_sel(nnper(1),:);
% B=popm_sel(nnper(2),:);
%%
for i=1:M*Pc*0.5
A=popm_sel(nnper(i),:);
B=popm_sel(nnper(i+1),:);
[A,B]=cross(A,B);
% popm_sel(nnper(1),:)=A;
% popm_sel(nnper(2),:)=B;
popm_sel(nnper(i),:)=A;
popm_sel(nnper(i+1),:)=B;
end
%%变异操作
for i=1:M
pick=rand;
while pick==0
pick=rand;
end
if pick<=Pmutation
popm_sel(i,:)=Mutation(popm_sel(i,:));
end
end
%%求适应度函数
NN=size(popm_sel,1);
len=zeros(NN,1);
for i=1:NN
len(i,1)=myLength(D,popm_sel(i,:));
end
maxlen=max(len);
minlen=min(len);
distance_min(iter+1,1)=minlen;
fitness=fit(len,m,maxlen,minlen);
rr=find(len==minlen);
fprintf('minlen=%d\n',minlen);
R=popm_sel(rr(1,1),:);
for i=1:N
fprintf('%d ',R(i));
end
fprintf('\n');
popm=[];
popm=popm_sel;
iter=iter+1;
%pause(1);
end
%end of while
%figure(3)
subplot(2,2,3);
plot_route(pos,R);
axis([-3 3 -3 3]);
title('图c');
%figure(4)
subplot(2,2,4);
plot(distance_min);
title('图d');
三、结果与分析
为方便测试参数,需要对同一批城市样本数据进行处理,保存随机序列到"citys.txt"文件中(后续调试使用语句"pos=load(‘citys.txt’);"):
pos=randn(N,2);
fid=fopen('citys.txt','wt');%写入文件路径
[m,n]=size(pos);
for i=1:1:m
for j=1:1:n
if j==n
fprintf(fid,'%g\n',pos(i,j));
else
fprintf(fid,'%g\t',pos(i,j));
end
end
end
fclose(fid);
3.1 种群规模对算法性能的影响
种群规模是遗传算法的一个参数,我们在求解TSP问题中选取的种群规模并没有一定依据,总是按照经验或者习惯来进行选取,在改进算法性能时,我们往往会选择优化交叉变异的算子而忽略种群规模。事实上,种群规模对遗传算法性能是有影响的,下面通过实验结果分析说明。
固定参数:
| 迭代次数ITER | 城市个数N | 交叉概率Pc | 变异概率Pmutation |
|---|---|---|---|
| 2000 | 25 | 0.8 | 0.05 |
变参:种群个数M
M=10(可得结果:路径长度收敛迭代次数为1939,最短距离为20.94)


M=30(可得结果:路径长度收敛迭代次数为863,最短距离为20.89)


M=50(可得结果:路径长度收敛迭代次数为764,最短距离为20.54)


M=80(可得结果:路径长度收敛迭代次数为255,最短距离为20.52)
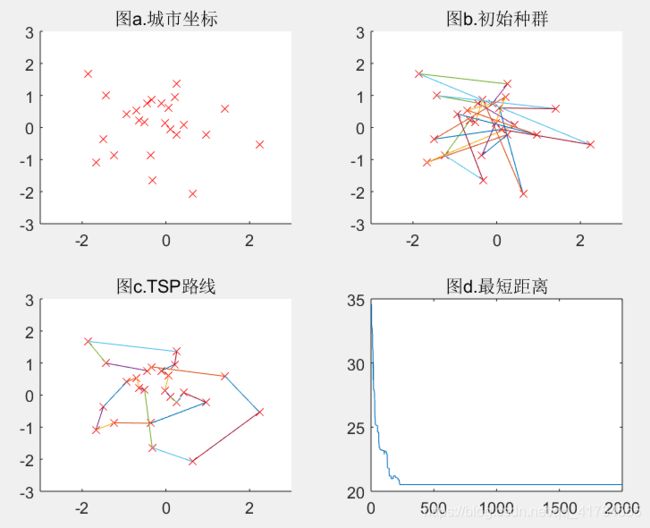

M=100(可得结果:路径长度收敛迭代次数为358,最短距离为18.93)
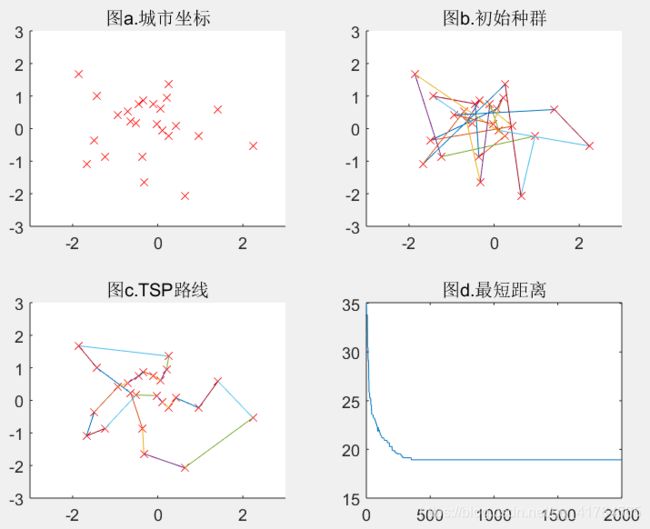

结论:如以上五组运行结果所示,分别取种群数量为10、30、50、80、100,从直观上看,当种群规模增大时,算法的计算时间,也就是收敛时间将会增大;而种群规模如果增大了,那么算法收敛到最优解的可能性就会增大,即全局搜索能力会增强;再者,当种群规模增大了,在解空间中搜索时,可以在相对较少的代数中找到最优解,那么进化代数也随着种群规模的增大而变小了。可得种群规模越大算法结果越精确,适应度越好,但运行时间越久。
3.2 城市序列对算法性能的影响
对于同一个城市样本,当城市序列改变时,对结果同样有影响,城市序列采用随机生成:
popm(i,:)=randperm(N);%随机排列,比如[2 4 5 6 1 3]
固定参数:
| 迭代次数ITER | 城市个数N | 种群个数M | 交叉概率Pc | 变异概率Pmutation |
|---|---|---|---|---|
| 2000 | 25 | 100 | 0.8 | 0.05 |
更新多次,可以得到不同的结果:
| 更新次数 | 城市初始序列 | 最短距离 | 运行时间 |
|---|---|---|---|
| 1 | 13 11 5 12 15 20 8 2 22 7 10 17 9 3 16 24 1 21 18 19 4 6 25 14 23 | 20.04 | 27.135s |
| 2 | 13 16 10 12 18 22 24 19 3 9 6 8 4 14 25 2 20 5 23 21 1 7 17 11 15 | 18.96 | 30.615s |
| 3 | 3 16 5 23 25 24 1 21 20 22 15 2 19 10 4 14 7 13 12 18 8 6 9 11 17 | 18.79 | 32.351s |
| 4 | 14 25 22 10 11 19 2 6 8 20 17 16 23 5 7 4 18 24 21 13 1 9 15 12 3 | 20.93 | 34.075s |
| 5 | 22 20 25 19 7 23 18 5 13 4 3 24 15 16 11 17 9 6 12 2 1 8 21 10 14 | 20.32 | 32.399s |
3.3 城市个数对算法性能的影响
固定参数:
| 迭代次数ITER | 种群个数M | 交叉概率Pc | 变异概率Pmutation |
|---|---|---|---|
| 2000 | 100 | 0.8 | 0.05 |
变参:城市个数N
| 城市个数 | 最短距离 | 运行时间 | 路径长度收敛时迭代次数 |
|---|---|---|---|
| 25 | 18.76 | 30.837s | 672 |
| 40 | 24.95 | 39.864s | 941 |
| 60 | 37.72 | 41.530s | 1782 |
| 80 | 52.61 | 45.658s | 1836 |
| 100 | 62.24 | 59.637s | 1967 |
结论:如上述统计结果,随着城市个数的增加,路径长度收敛时迭代次数越来越多,逼近2000次,运行时间也越来越长。因此,当城市数量较多时,遗传算法显然无法优化解决TSP问题,这时可以考虑其他求解方法,如蚁群算法。
3.4 交叉概率对算法性能的影响
交叉概率用于判断两两个体是否需要交叉,在一次进化迭代中,交叉通常是采用两两互相不重复交叉的方式,当然也可采用随机交叉的方式,这时的交叉次数不能确定。
固定参数:
| 迭代次数ITER | 城市个数N | 种群个数M | 变异概率Pmutation |
|---|---|---|---|
| 2000 | 25 | 100 | 0.05 |
变参:交叉概率Pc
Pc=0.001(可得结果:路径长度收敛迭代次数为977,最短距离为20.78)
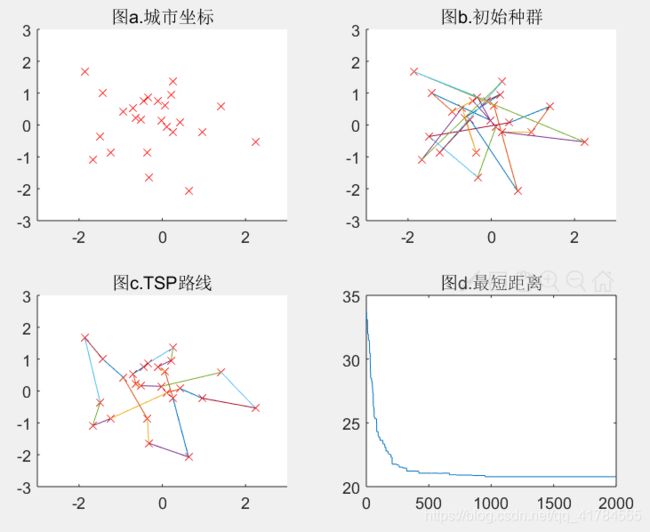

Pc=0.1(可得结果:路径长度收敛迭代次数为785,最短距离为21.37)
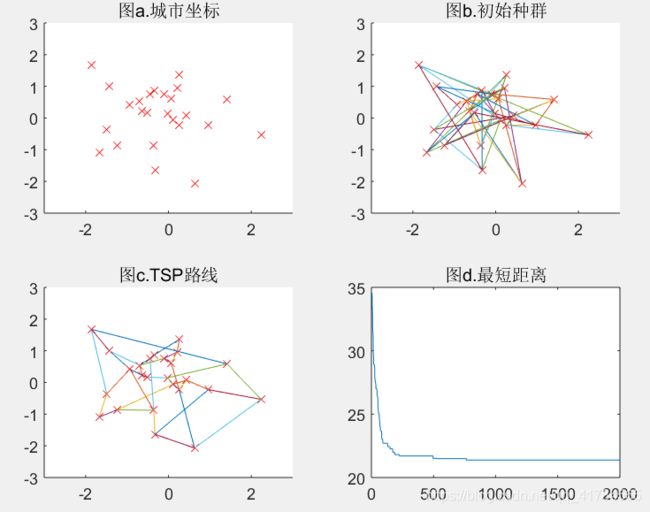

Pc=0.3(可得结果:路径长度收敛迭代次数为536,最短距离为20.86)
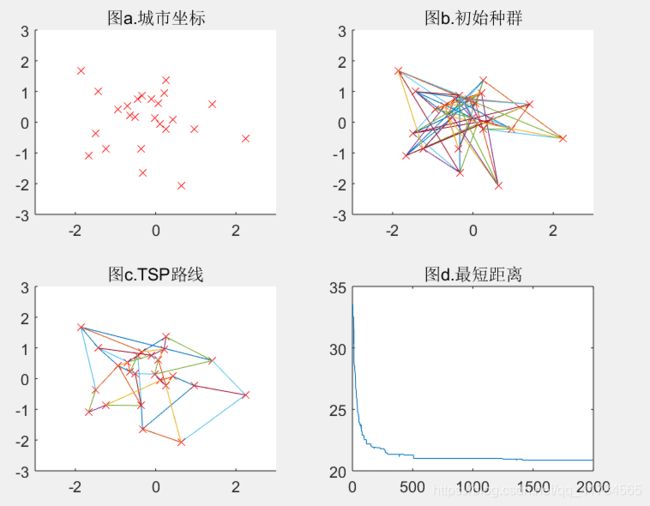
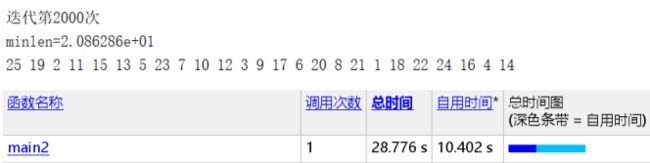
Pc=0.8(可得结果:路径长度收敛迭代次数为970,最短距离为18.46)
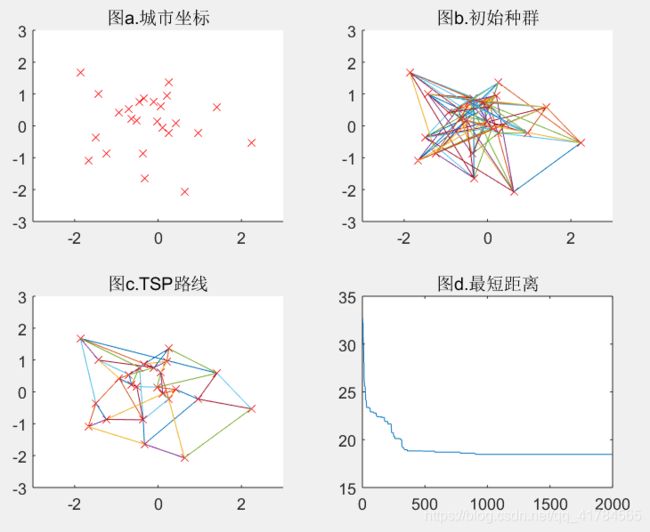

Pc=0.95(可得结果:路径长度收敛迭代次数为632,最短距离为18.68)


结论:如以上五组运行结果所示,分别取交叉概率为0.001、0.1、0.3、0.8、0.95,可以看出,当交叉概率过小,如前三组,都不能得到最优解,当交叉概率取较大值0.8、0.95时,得到的结果更优。可得交叉概率过低将不能得到最优解,交叉概率较大时,平均适应度越好,结果越优。
3.5 变异概率对算法性能的影响
变异概率用于判断任一个体是否需要变异。
固定参数:
| 迭代次数ITER | 城市个数N | 种群个数M | 交叉概率Pc |
|---|---|---|---|
| 2000 | 25 | 100 | 0.8 |
变参:变异概率Pmutation
Pmutation=0.001(可得结果:路径长度收敛迭代次数为1796,最短距离为21.91)
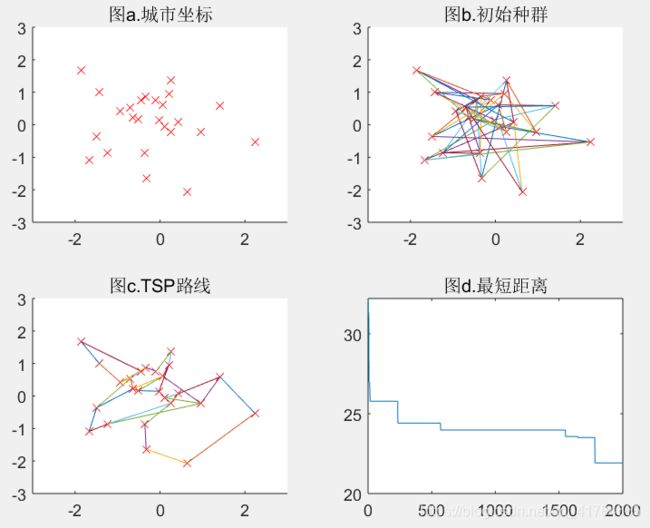
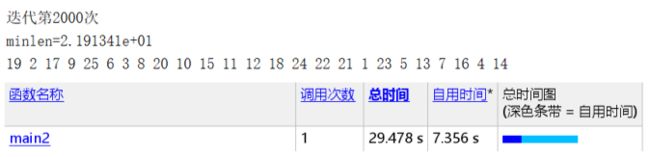
Pmutation=0.05(可得结果:路径长度收敛迭代次数为372,最短距离为19.84)
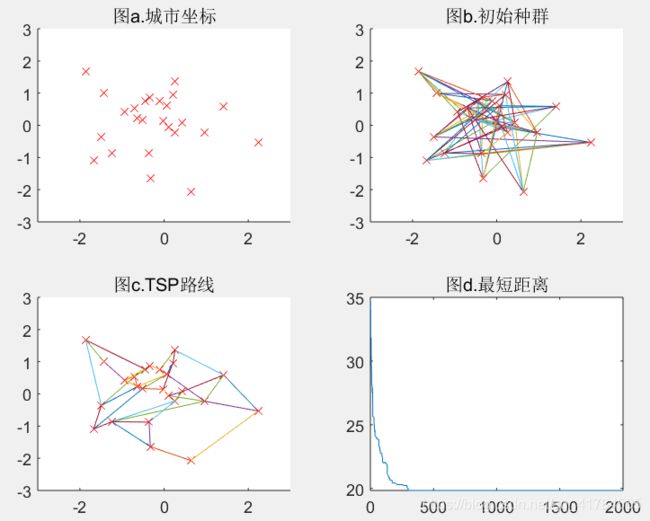

Pmutation=0.2(可得结果:路径长度收敛迭代次数为1949,最短距离为18.6)
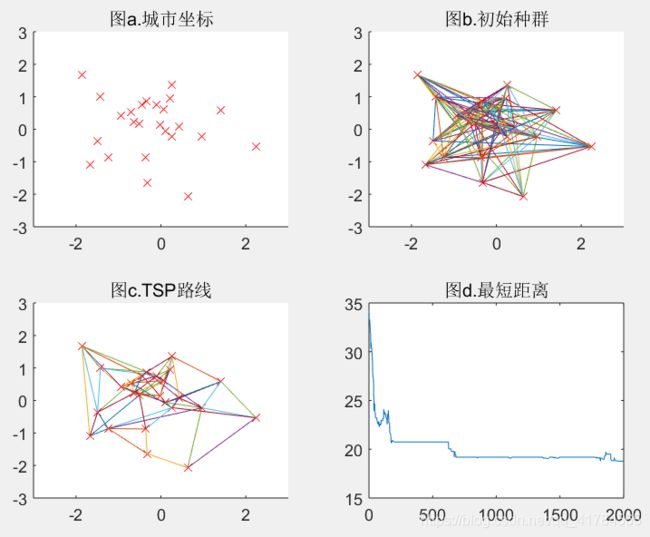

Pmutation=0.5(可得结果:路径长度收敛迭代次数为1997,最短距离为18.0)


Pmutation=0.9(可得结果:路径长度收敛迭代次数为1796,最短距离为21.91)
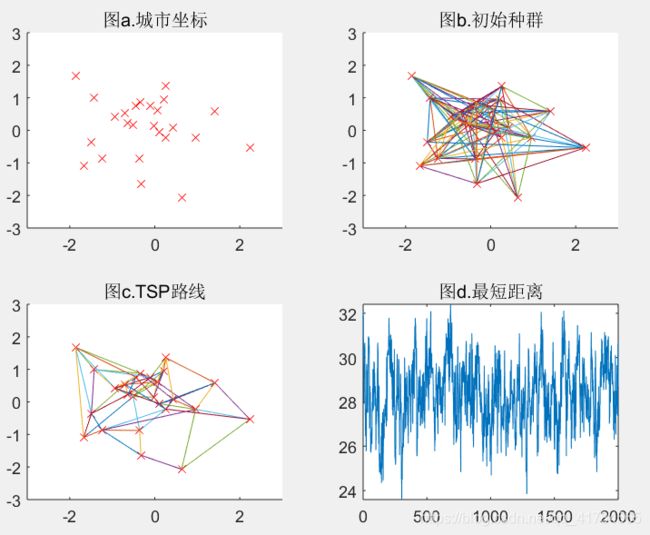
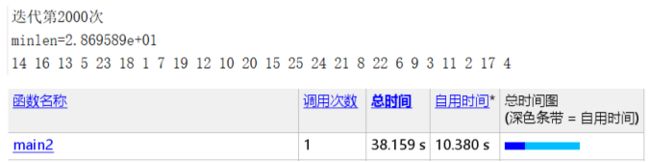
结论:如以上五组运行结果所示,分别取变异概率为0.001、0.05、0.2、0.5、0.9,可以看出变异概率越大,适应度函数变化越剧烈,最短距离图像随着迭代次数增加会来回波动,而不是递减趋势,当变异概率过小(如0.001)或过大(如0.9)时,都将导致无法得到最优解。
四、小结(注意点)
- 对于任何一个具体的优化问题,调节遗传算法的参数可能会有利于更好更快收敛,这些参数包括个体数目、种群规模、交叉率和变异率。例如太大的变异率会导致丢失最优解,而过小的变异率会导致算法过早的收敛于局部最优点。
- 对TSP问题的求解有多种方法,遗传算法不一定总是最优的算法,例如当城市数量较多时遗传算法就很难得到最优解,这时可以尝试其他算法或几种算法互相补充。
- 遗传算法在适应度函数选择不当的情况下有可能收敛于局部最优,而不能达到全局最优。