LeetCode_11_树----中序与后序遍历构建二叉树(重点收藏)
大家好!我是你们的好朋友,大数据老虾。相遇是缘,既然来了就拎着小板凳坐下来一起唠会儿,如果在文中有所收获,请别忘了一键三连,你的鼓励,是我创作的动力,废话不多说,直接开干 吧。
先别急着走,文末干货,记得拎着小板凳离开的时候也给它顺走
树-中序与后序遍历构建二叉树
- 中序与后序遍历构建二叉树
-
- 题目
- 图解遍历方式详解
- 树的还原过程
- 树的还原过程变量定义
- 位置关系的计算
- 还原过程
- Java实现代码
- 方法1:递归
- C++s实现代码
- 算法
- Java实现代码
- 复杂度分析
- Python实现代码
- 方法2:迭代
- 具体实现
- 算法流程
- Java实现代码
-
- 复杂度分析
- 文末彩蛋
中序与后序遍历构建二叉树
题目
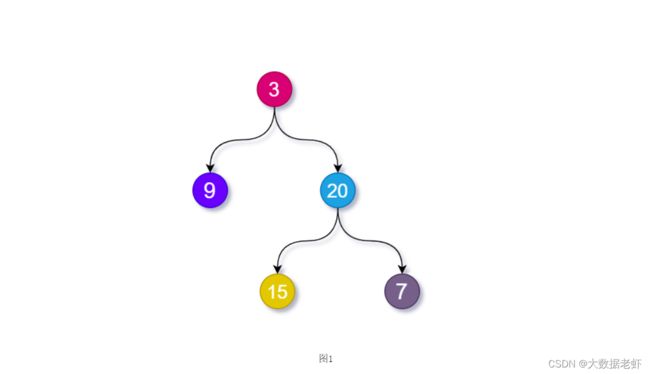
给出两个整数数组,inorder 和 postorder,其中 inorder 是二叉树的中序遍历,postorder是同一棵树的后序遍历,构建并返回这棵二叉树。
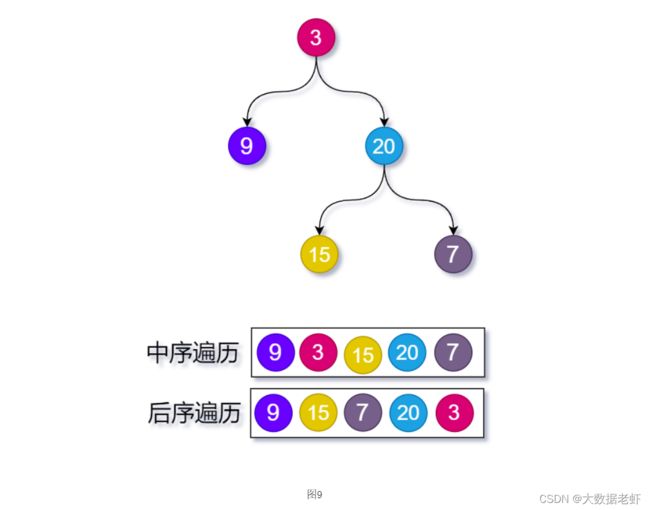
input:inorder = [9, 3, 15, 20, 7], postorder = [9, 15, 7, 20, 3]
output:[3, 9, 20, null, null, 15, 7]
示例2:
input:inorder = [-1], postorder = [-1]
output:[-1]
图解遍历方式详解
先进行中序遍历和后序遍历二叉树,然后再根据遍历结果将二叉树进行还原。

中序遍历:
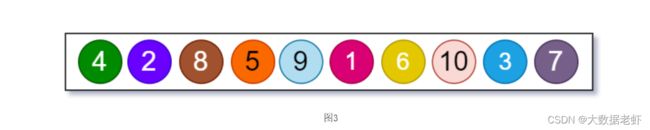
后序遍历:

根据中序和后序遍历结果还原二叉树:
中序遍历和后续遍历的特性
1、在后序遍历序列中,最后一个元素为树的根节点
2、在中序遍历序列中,根节点的左边为左子树,根节点的右边为右子树
树的还原过程
根据中序遍历和后续遍历的特性进行树的还原过程分析:
1、首先在后序遍历序列中找到根节点(最后一个元素)
2、根据根节点在中序遍历序列中找到根节点的位置
3、根据根节点的位置将中序遍历序列分为左子树和右子树
4、根据根节点的位置确定左子树和右子树在中序数组和后续数组中的左右边界位置
5、递归构造左子树和右子树
6、返回根节点结束
树的还原过程变量定义
定义变量帮助进行树的还原:
1、HashMap memo 需要哈希表来保存中序遍历序列中,元素和索引的位置关系。因为从后序序列中拿到根节点后,要在中序序列中查找对应的位置,从而将数组分为左子树和右子树
2、int ri 根节点在中序遍历数组中的索引。
3、中序遍历数组的两个位置标记 [is, ie],is 是起始位置,ie 是结束位置
4、后序遍历数组的两个位置标记 [ps, pe] ps 是起始位置,pe 是结束位置
位置关系的计算
在找到根节点位置以后,要定下一轮中,左子树和右子树在中序数组和后续数组中的左右边界的位置。
1、左子树-中序数组 is = is, ie = ri - 1
2、左子树-后序数组 ps = ps, pe = ps + ri - is - 1 (pe计算过程解释,后续数组的起始位置加上左子树长度-1 就是后后序数组结束位置了,左子树的长度 = 根节点索引-左子树)
3、右子树-中序数组 is = ri + 1, ie = ie
4、右子树-后序数组 ps = ps + ri - is, pe - 1
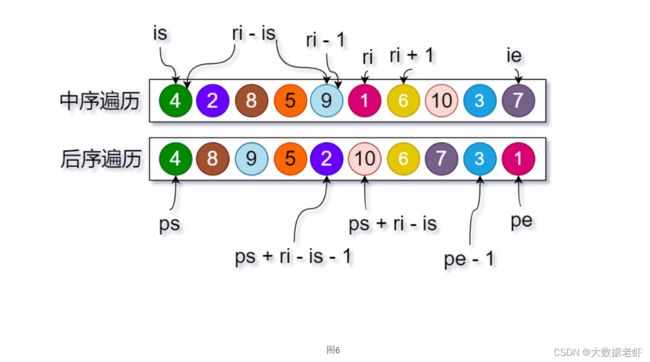
还原过程
Java实现代码
class Solution {
HashMap<Integer,Integer> memo = new HashMap<>();
int[] post;
public TreeNode buildTree(int[] inorder, int[] postorder) {
for(int i = 0;i < inorder.length; i++) memo.put(inorder[i], i);
post = postorder;
TreeNode root = buildTree(0, inorder.length - 1, 0, post.length - 1);
return root;
}
public TreeNode buildTree(int is, int ie, int ps, int pe) {
if(ie < is || pe < ps) return null;
int root = post[pe];
int ri = memo.get(root);
TreeNode node = new TreeNode(root);
node.left = buildTree(is, ri - 1, ps, ps + ri - is - 1);
node.right = buildTree(ri + 1, ie, ps + ri - is, pe - 1);
return node;
}
}
方法1:递归
解析:
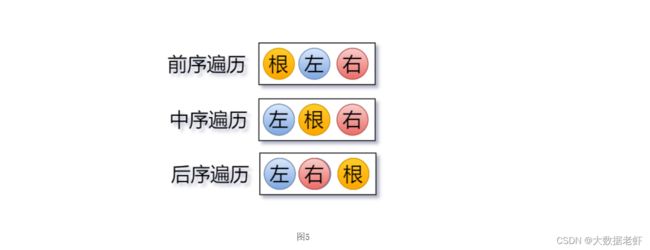
如何进行中序遍历和后序遍历
- 中序遍历的顺序是每次遍历左孩子,再遍历根节点,最后遍历右孩子。
- 后序遍历的顺序是每次遍历左孩子,再遍历右孩子,最后遍历根节点。
C++s实现代码
// 中序遍历
void inorder(TreeNode* root) {
if (root == nullptr) {
return;
}
inorder(root->left);
ans.push_back(root->val);
inorder(root->right);
}
// 后序遍历
void postorder(TreeNode* root) {
if (root == nullptr) {
return;
}
postorder(root->left);
postorder(root->right);
ans.push_back(root->val);
}
//*************************************************************************
// 【前序】遍历算法
//二叉树不空,先访问根结点,然后前序遍历左子树,再前序遍历右子树
//*************************************************************************
void PreOrderTraverse(BiTree T)
{
if(T == NULL) /* 递归跳出条件*/
return;
printf("%c", T ->data); /* 对结点进行操作(可替换成其它操作)*/
PreOrderTraverse(T ->lchild); /* 先序遍历左子树*/
PreOrderTraverse(T ->rchild); /* 先序遍历右字树*/
}
//*************************************************************************
// 【中序】遍历算法
//二叉树不空,从根结点开始(并非是先访问根结点),中序遍历根节点的左子树,
//然后访问根结点,最后中序遍历该根结点的右子树
//*************************************************************************
void InOrderTraverse(BiTree T)
{
if(T == NULL) /* 递归跳出条件*/
return;
InOrderTraverse(T ->lchild); /* 中序遍历左子树*/
printf("%c", T ->data); /* 对结点进行操作(可替换成其它操作)*/
InOrderTraverse(T ->rchild); /* 中序遍历右字树*/
}
//*************************************************************************
// 【后序】遍历算法
//二叉树不空,从左到右先叶子后结点的方式遍历左右子树,最后遍历根结点
//*************************************************************************
void PostOrderTraverse(BiTree T)
{
if(T == NULL) /* 递归跳出条件*/
return;
PostOrderTraverse(T ->lchild); /* 后序遍历左子树*/
PostOrderTraverse(T ->rchild); /* 后序遍历右字树*/
printf("%c", T ->data); /* 对结点进行操作(可替换成其它操作)*/
}
根据上文所述,可以发现后序遍历的数组最后一个元素代表的即为根节点。
知道这个性质后,可以利用已知的根节点信息在中序遍历的数组中找到根节点所在的下标,然后根据其将中序遍历的数组分成左右两部分,左边部分即左子树,右边部分为右子树,针对每个部分可以用同样的方法继续递归下去构造。
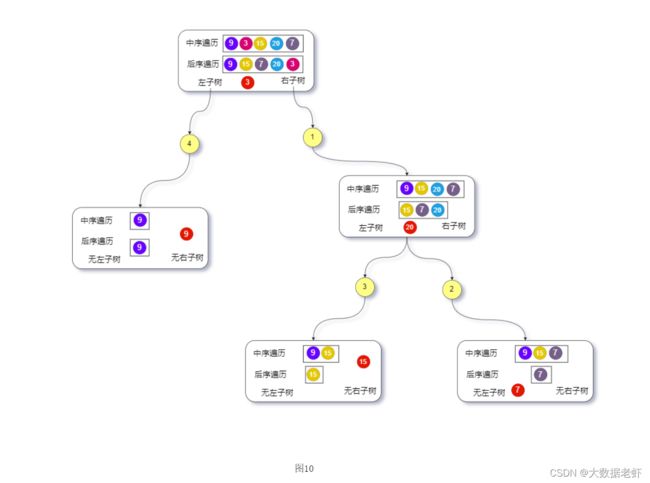
算法
为了高效查找根节点元素在中序遍历数组中的下标,选择创建哈希表来存储中序序列,即建立一个(元素,下标)键值对的哈希表。
定义递归函数 helper(in_left, in_right) 表示当前递归到中序序列中当前子树的左右边界,递归入口为helper(0, n - 1) :
1、如果 in_left > in_right,说明子树为空,返回空节点。
2、选择后序遍历的最后一个节点作为根节点。
3、利用哈希表 O(1) 查询当根节点在中序遍历中下标为 index。从 in_left 到 index - 1 属于左子树,从 index + 1 到 in_right 属于右子树。
4、根据后序遍历逻辑,递归创建右子树 helper(index + 1, in_right) 和左子树 helper(in_left, index - 1)。
PS:注意这里有需要先创建右子树,再创建左子树的依赖关系。可以理解为在后序遍历的数组中整个数组是先存储左子树的节点,再存储右子树的节点,最后存储根节点,如果按每次选择「后序遍历的最后一个节点」为根节点,则先被构造出来的应该为右子树。
5、返回根节点 root。
Java实现代码
class Solution {
int post_idx;
int[] postorder;
int[] inorder;
Map<Integer, Integer> idx_map = new HashMap<Integer, Integer>();
public TreeNode helper(int in_left, int in_right) {
// 如果这里没有节点构造二叉树了,就结束
if (in_left > in_right) {
return null;
}
// 选择 post_idx 位置的元素作为当前子树根节点
int root_val = postorder[post_idx];
TreeNode root = new TreeNode(root_val);
// 根据 root 所在位置分成左右两棵子树
int index = idx_map.get(root_val);
// 下标减一
post_idx--;
// 构造右子树
root.right = helper(index + 1, in_right);
// 构造左子树
root.left = helper(in_left, index - 1);
return root;
}
public TreeNode buildTree(int[] inorder, int[] postorder) {
this.postorder = postorder;
this.inorder = inorder;
// 从后序遍历的最后一个元素开始
post_idx = postorder.length - 1;
// 建立(元素,下标)键值对的哈希表
int idx = 0;
for (Integer val : inorder) {
idx_map.put(val, idx++);
}
return helper(0, inorder.length - 1);
}
}
public class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode() {}
TreeNode(int val) { this.val = val; }
TreeNode(int val, TreeNode left, TreeNode right) {
this.val = val;
this.left = left;
this.right = right;
}
}
复杂度分析
-
时间复杂度:O(n),其中 n 是树中的节点个数。
-
空间复杂度:O(n)。需要使用 O(n) 的空间存储哈希表,以及 O(h)(其中 hh 是树的高度)的空间表示递归时栈空间。这里 h
Python实现代码
class Solution:
def buildTree(self, inorder: List[int], postorder: List[int]) -> TreeNode:
def helper(in_left, in_right):
# 如果这里没有节点构造二叉树了,就结束
if in_left > in_right:
return None
# 选择 post_idx 位置的元素作为当前子树根节点
val = postorder.pop()
root = TreeNode(val)
# 根据 root 所在位置分成左右两棵子树
index = idx_map[val]
# 构造右子树
root.right = helper(index + 1, in_right)
# 构造左子树
root.left = helper(in_left, index - 1)
return root
# 建立(元素,下标)键值对的哈希表
idx_map = {val:idx for idx, val in enumerate(inorder)}
return helper(0, len(inorder) - 1)
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
方法2:迭代
解析:
迭代法是一种非常巧妙的实现方法,迭代法的实现基于以下两点发现
- 如果将中序遍历反序,则得到反向的中序遍历,即每次遍历右孩子,再遍历根节点,最后遍历左孩子。
- 如果将后序遍历反序,则得到反向的前序遍历,即每次遍历根节点,再遍历右孩子,最后遍历左孩子。
PS: 「反向」的意思是交换遍历左孩子和右孩子的顺序,即反向的遍历中,右孩子在左孩子之前被遍历。
对于后序遍历中的任意两个连续节点 u 和 v(在后序遍历中,u 在 v 的前面),根据后序遍历的流程,可以知道 u 和 v 只有两种可能的关系:
1、u 是 v 的右儿子。这是因为在遍历到 u 之后,下一个遍历的节点就是 u 的双亲节点,即 v;
2、v 没有右儿子,并且 u 是 v 的某个祖先节点(或者 v 本身)的左儿子。如果 v 没有右儿子,那么上一个遍历的节点就是 v 的左儿子。如果 v 没有左儿子,则从 v 开始向上遍历 v 的祖先节点,直到遇到一个有左儿子(且 v 不在它的左儿子的子树中)的节点va ,那么 u 就是 va 的左儿子。
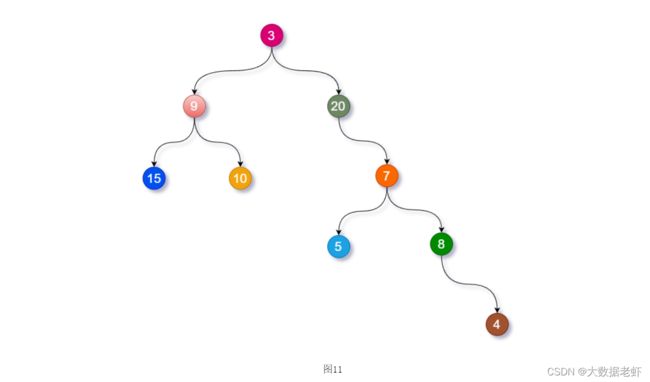
中序遍历
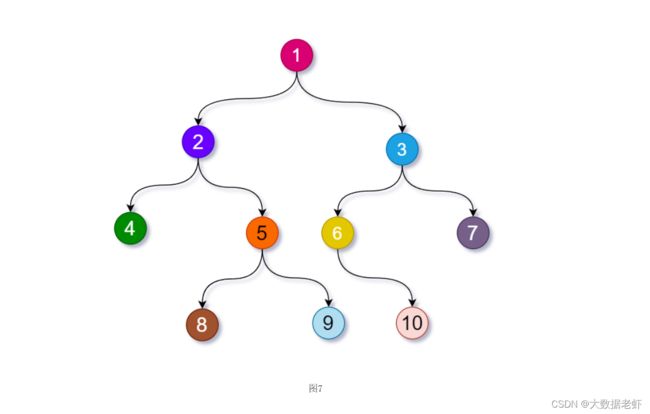
inorder = [15, 9, 10, 3, 20, 5, 7, 8, 4]
后序遍历
postorder = [15, 10, 9, 5, 4, 8, 7, 20, 3]
用一个栈 stack 来维护「当前节点的所有还没有考虑过左儿子的祖先节点」,栈顶就是当前节点。也就是说,只有在栈中的节点才可能连接一个新的左儿子。同时,用一个指针 index 指向中序遍历的某个位置,初始值为 n - 1,其中 n 为数组的长度。index 对应的节点是「当前节点不断往右走达到的最终节点」,这也是符合反向中序遍历的,它的作用在下面的过程中会有所体现。
具体实现
首先将根节点 3 入栈,再初始化 index 所指向的节点为 4,随后对于后序遍历中的每个节点,依次判断它是栈顶节点的右儿子,还是栈中某个节点的左儿子。
1、遍历 20。20 一定是栈顶节点 3 的右儿子。使用反证法,假设 20 是 3 的左儿子,因为 20 和 3 中间不存在其他的节点,那么 3 没有右儿子,index 应该恰好指向 3,但实际上为 4,因此产生了矛盾。所以将 20 作为 3 的右儿子,并将 20 入栈。
- stack = [3, 20]
- index -> inorder[8] = 4
2、遍历 7,8 和 4。同理可得它们都是上一个节点(栈顶节点)的右儿子,所以它们会依次入栈。
- stack = [3, 20, 7, 8, 4]
- index -> inorder[8] = 4
3、遍历 5。发现 index 恰好指向当前的栈顶节点 4,也就是说 4 没有右儿子,那么 5 必须为栈中某个节点的左儿子。那么如何找到这个节点呢?栈中的节点的顺序和它们在反向前序遍历中出现的顺序是一致的,而且每一个节点的左儿子都还没有被遍历过,那么这些节点的顺序和它们在反向中序遍历中出现的顺序一定是相反的。
这是因为栈中的任意两个相邻的节点,前者都是后者的某个祖先。并且我们知道,栈中的任意一个节点的左儿子还没有被遍历过,说明后者一定是前者右儿子的子树中的节点,那么后者就先于前者出现在反向中序遍历中。
因此我们可以把 index 不断向左移动,并与栈顶节点进行比较。如果 index 对应的元素恰好等于栈顶节点,那么说明在反向中序遍历中找到了栈顶节点,所以将 index 减少 1 并弹出栈顶节点,直到 index 对应的元素不等于栈顶节点。按照这样的过程,弹出的最后一个节点 x 就是 5 的双亲节点,这是因为 5 出现在了 x 与 x 在栈中的下一个节点的反向中序遍历之间,因此 5 就是 x 的左儿子。
4、回到例子,会依次从栈顶弹出 4,8 和 7,并且将 index 向左移动了三次。将 5 作为最后弹出的节点 7 的左儿子,并将 5 入栈。
- stack = [3, 20, 5]
- index -> inorder[5] = 5
5、遍历 9。同理,index 恰好指向当前栈顶节点 5,那么会依次从栈顶弹出 5,20 和 3,并且将 index 向左移动了三次。将 9 作为最后弹出的节点 3 的左儿子,并将 9 入栈。
- stack = [9]
- index -> inorder[2] = 10
6、遍历 10,将 10 作为栈顶节点 9 的右儿子,并将 10 入栈。
- stack = [9, 10]
- index -> inorder[2] = 10
7、遍历 15。index 恰好指向当前栈顶节点 10,那么会依次从栈顶弹出 10 和 9,并且将 index 向左移动了两次。将 15 作为最后弹出的节点 9 的左儿子,并将 15 入栈。
- stack = [15]
- index -> inorder[0] = 15
此时遍历结束,就构造出了正确的二叉树。
算法流程
归纳出上述例子中的算法流程:
1、用一个栈和一个指针辅助进行二叉树的构造。初始时栈中存放了根节点(后序遍历的最后一个节点),指针指向中序遍历的最后一个节点;
2、依次枚举后序遍历中除了第一个节点以外的每个节点。如果 index 恰好指向栈顶节点,那么不断地弹出栈顶节点并向左移动 index,并将当前节点作为最后一个弹出的节点的左儿子;如果 index 和栈顶节点不同,将当前节点作为栈顶节点的右儿子;
3、无论是哪一种情况,最后都将当前的节点入栈。
Java实现代码
class Solution {
public TreeNode buildTree(int[] inorder, int[] postorder) {
if (postorder == null || postorder.length == 0) {
return null;
}
TreeNode root = new TreeNode(postorder[postorder.length - 1]);
Deque<TreeNode> stack = new LinkedList<TreeNode>();
stack.push(root);
int inorderIndex = inorder.length - 1;
for (int i = postorder.length - 2; i >= 0; i--) {
int postorderVal = postorder[i];
TreeNode node = stack.peek();
if (node.val != inorder[inorderIndex]) {
node.right = new TreeNode(postorderVal);
stack.push(node.right);
} else {
while (!stack.isEmpty() && stack.peek().val == inorder[inorderIndex]) {
node = stack.pop();
inorderIndex--;
}
node.left = new TreeNode(postorderVal);
stack.push(node.left);
}
}
return root;
}
}
public class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode() {}
TreeNode(int val) { this.val = val; }
TreeNode(int val, TreeNode left, TreeNode right) {
this.val = val;
this.left = left;
this.right = right;
}
}
复杂度分析
-
时间复杂度:O(n),其中 nn 是树中的节点个数。
-
空间复杂度:O(n),需要使用 O(h)(其中 h 是树的高度)的空间存储栈。这里 h
文末彩蛋
找资料很累吧,别急客官,俺统统安排上。程序员不可缺少的书籍,程序员经典名言:"收藏了就等于学会啦"
图灵程序丛书300+
Linux实战100讲
Linux书籍
计算机基础硬核总结
计算机基础相关书籍
操作系统硬核总结
Java自学宝典
Java学习资料
Java硬核资料
Java面试必备
Java面试深度剖析
阿里巴巴Java开发手册
MySQL入门资料
MySQL进阶资料
深入浅出的SQL
Go语言书籍
我的个人仓库:私人仓库