图论--图的存储及遍历

图的概念

简单讲，一个图是由一些点和这些点之间的连线组成的。严格意义讲，图是一种数据结构，定义为：graph=（V，E）。V 是一个非空有限集合，代表顶点，E 代表边的集合，一般用（Vx,Vy）表示，其中，Vx，Vy属于V。
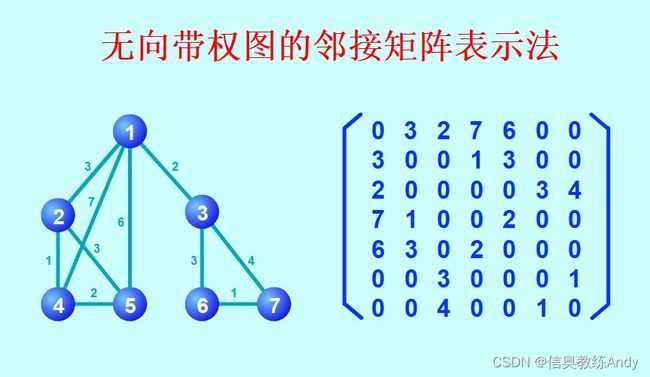
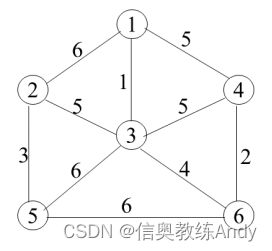
无向图
如果边是没有方向的，称为无向图，如右图。边用一对圆括号表示，如：（Vx,Vy），（Vy,Vx），当然这两者是等价的。并且说边（Vx,Vy）依附于（相关联）顶点Vx和Vy。
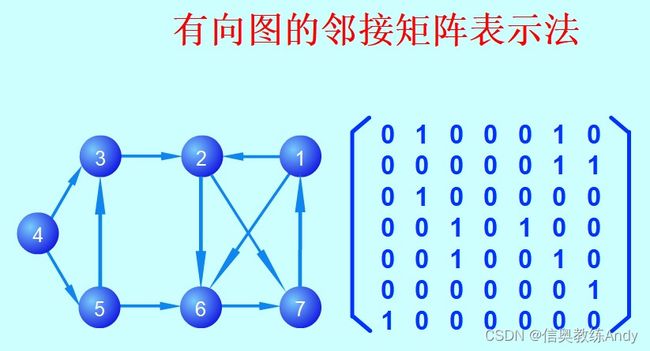
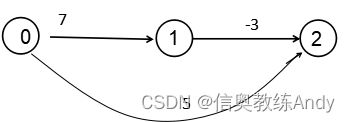
有向图
如果边是带箭头的，则称为有向图，如左图。边用一对尖括号表示，此时与是不同的，如的起点为Vx，终点为Vy。有向图中的边又称为弧。起点称为弧头、终点称为弧尾。

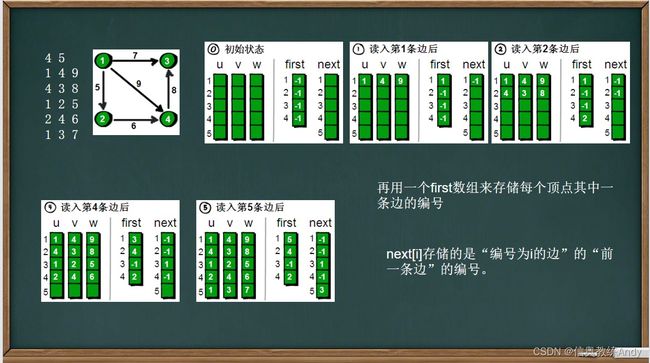
图的存储方式

1、邻接矩阵

#include
using namespace std;
int a[10][10]={0};
int main()
{
	int n,m;
	cin>>n>>m;
	int u,v,w;
	for(int i=1;i<=m;i++)//读入m条边 
	{
		cin>>u>>v>>w;
		a[u][v]=a[v][u]=w; //无向图	
	}
	for(int i=1;i<=n;i++)//输出邻接矩阵 
    { 	
    	for(int j=1;j<=n;j++)
	{
		cout<<a[i][j]<<" ";
	} 
	cout<<endl;
	}
	return 0;
}

2、邻接表及遍历

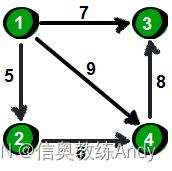
第一行两个整数n m。n表示顶点个数（顶点编号为1~n），m表示边的条数。 接下来m行表示，每行有3个数x y
z，表示顶点x到顶点y的边的权值为z。
4 5
1 4 9
4 3 8
1 2 5
2 4 6
1 3 7

顶点集 边集

int n,m,i;
 //u、v和w的数组大小要根据实际情况来设置，要比m的最大值要大1
int u[6],v[6],w[6];
 //first和next的数组大小要根据实际情况来设置，要比n的最大值要大1
 int first[5],next[6];
 scanf("%d %d",&n,&m);
 //初始化first数组下标1~n的值为-1，表示1~n顶点暂时都没有边
 for(i=1;i<=n;i++)
     first[i]=-1;
 for(i=1;i<=m;i++)
 {
     scanf("%d %d %d",&u[i],&v[i],&w[i]);//读入每一条边
     //下面两句是关键啦
     next[i]=first[u[i]];
     first[u[i]]=i;
 }

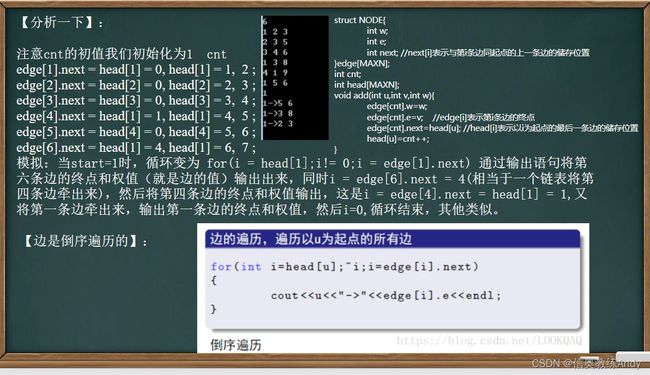
遍历1号顶点所有边的代码如下

k=first[1];// 1号顶点其中的一条边的编号（其实也是最后读入的边）
while(k!=-1) //其余的边都可以在next数组中依次找到
{
    printf("%d %d %d\n",u[k],v[k],w[k]);
    k=next[k];
}

遍历每个顶点的所有边的代码如下

for(i=1;i<=n;i++)
{
    k=first[i];
    while(k!=-1)
    {
        printf("%d %d %d\n",u[k],v[k],w[k]);
        k=next[k];
    }
}

完整代码

#include
#include
using namespace std;
const int E=50;//E为最大边数
const int N=10;//n为最大定点数
struct Edge {
    int u,v,w,next;//两顶点，权值，下一条边；
} edge[E];
int head[N];//表头；记录顶点的各个边 
int num;//内存指针；记录边号，已读入边的顺序从1开始为边编号 
void chushi()
{
    for(int i=1; i<=N; i++)
    head[i]=-1;
    num=1;
}
void add_edge(int b,int e,int w)
{
    edge[num].u=b;
    edge[num].v=e;
    //edge[num].w=w;
    edge[num].next=head[b];
    head[b]=num++;
}
int main() 
{
    int n,m,a,b,x;
    chushi();
    cin>>n>>m;
    for(int i=1;i<=m;i++)
    {
          cin>>a>>b>>x;   //a、b之间有一条长度为x的边 
          add_edge(a,b,x);
    }
    for(int j=1;j<=n;j++) 
    {
    	cout<<j;
    for(int i=head[j];i!=-1;i=edge[i].next)   //遍历从点j开始的所有边 
    {
           cout<<"-->"<<edge[i].next;//输出边号；cout<<"-->"<
    }
    cout<<endl;
	}
    
    return 0;
}

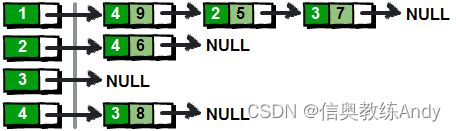
vector模拟邻接表

/*G就是整个图的邻接表。
遍历某个点的边表，举个例子
G[x]是一个数组，里面存的就是G[x]所有的点的序号，后插的顺序。
遍历这个点相邻的边时候，直接for(int i=0;i
#include 
using namespace std;
const int maxv=1e5+10;
const int maxe=1e5+10;
const int inf=0x3f3f3f3f;
int n;
bool vis[maxv];
vector<int> G[maxv];
void dfs(int x)
{
    if(!vis[x])
    {
        printf("%d ",x);
        vis[x]=1;
        for(int i=0;i<G[x].size();i++)
        {
            int d=G[x][i];
            if(!vis[d])
            {
                dfs(d);
            }
        }
    }
}
 int main()
{
    while(scanf("%d",&n)==1)
    {
        memset(vis,0,sizeof(vis));
        for(int i=1;i<=n-1;i++)
        {
            int s,d;
            scanf("%d%d",&s,&d);
            G[s].push_back(d);//无向图 
            G[d].push_back(s);
        }
        dfs(1);
    }
}

3、向前星
前向星是一种特殊的边集数组,我们把边集数组中的每一条边按照起点从小到大排序,如果起点相同就按照终点从小到大排序,并记录下以某个点为起点的所有边在数组中的起始位置和存储长度,那么前向星就构造好了.
它的优点是实现简单，容易理解，缺点是需要在所有边都读入完毕的情况下对所有边进行一次排序，带来了时间开销，实用性也较差，只适合离线算法。

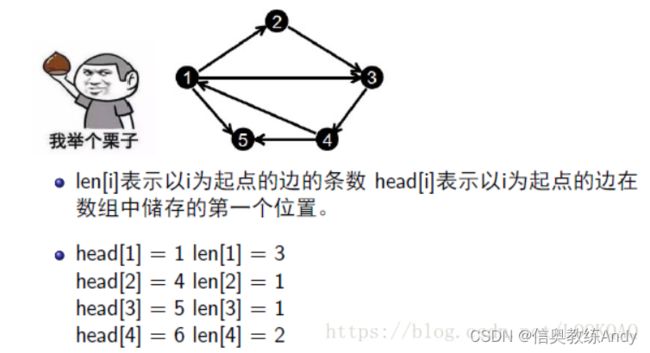
【前向星和链式前向星的不同】：
链式前向星（就是数组模拟链表）
链式前向星和邻接表类似，也是链式结构和线性结构的结合，每个结点i都有一个链表，链表的所有数据是从i出发的所有边的集合（对比邻接表存的是顶点集合），边的表示为一个四元组(u, v, w, next)，其中(u, v)代表该条边的有向顶点对，w代表边上的权值，next指向下一条边。

【给出链式前向星的代码实现】：
#include
using namespace std;
#define MAXN 100501
struct NODE{
	int w;
	int e;
	int next; //next[i]表示与第i条边同起点的上一条边的储存位置
}edge[MAXN];
int cnt;
int head[MAXN]; 
void add(int u,int v,int w){
	edge[cnt].w=w;
	edge[cnt].e=v;    //edge[i]表示第i条边的终点 
	edge[cnt].next=head[u]; //head[i]表示以i为起点的最后一条边的储存位置 
	head[u]=cnt++;
}
int main(){
	memset(head,0,sizeof(head));
	cnt=1;
	int n;
	cin>>n;
	int a,b,c;
	while(n--){
		cin>>a>>b>>c;
		add(a,b,c);
	}
	int start;
	cin>>start;
	for(int i=head[start];i!=0;i=edge[i].next)
	   cout<<start<<"->"<<edge[i].e<<" "<<edge[i].w<<endl;
	return 0;
}

图的遍历

图的遍历跟图的存储方式有很大的相关性。如果使用邻接表进行图的存储，那么遍历方式就如上面展示那样。而使用邻接矩阵存储的图的遍历方式，一般有深度优先遍历和广度优先遍历两种。
例题1：查找文献
例题2：图的遍历

练习题目

1、信息传递
2、幻象迷宫