归并排序_非递归 / 递归(C语言)

数据结构总目录

归并排序

归并排序是建立在归并操作上的一种有效的排序算法,该算法是采用分治法的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为二路归并。

1. 归并算法

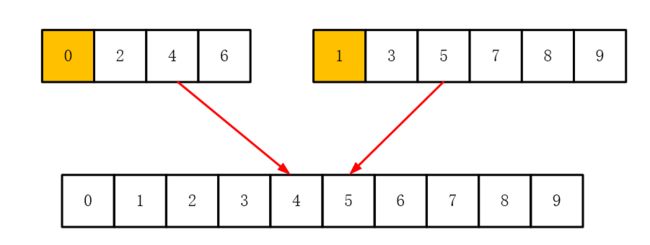
1.1 图文解析

归并：将两个有序的子序列进行合并，得到一个完全有序的序列

1.2 源代码

#include
#define left 4
#define right 6  

int main()
{
    int num1[left] = {0, 2, 4, 6};
    int num2[right] = {1, 3, 5, 7, 8, 9};
    
    int sort[left + right];
    
    int i = 0, j = 0, k = 0;
    while (i < left && j < right)
    {
        if (num1[i] < num2[j])
        {
            sort[k++] = num1[i++];
        }
        else
        {
            sort[k++] = num2[j++];
        }
    }

    while (i < left)
    {
        sort[k++] = num1[i++];
    }
    while (j < right)
    {
        sort[k++] = num2[j++];
    }
    
    for (i = 0; i < k; i++)
    {
        printf("%d ", sort[i]);
    }
    printf("\n");
    return 0;
}

1.3 测试结果

2. 归并排序—非递归

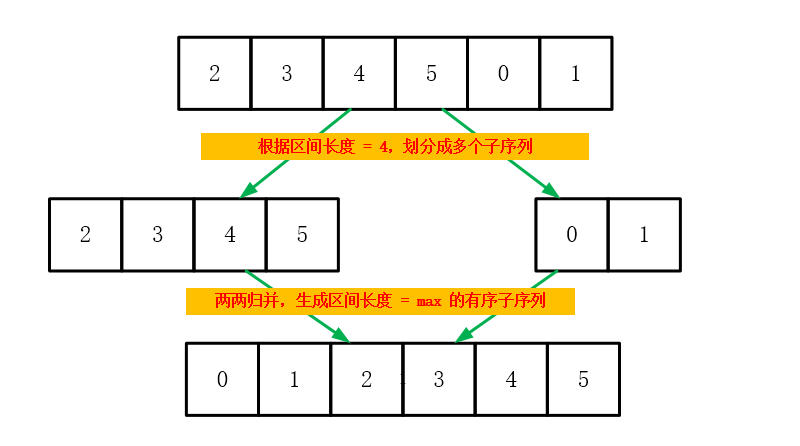
2.1 图文解析

非递归的归并排序主要在于子序列区间的划分，若直接对半分，则两个子序列都可能不是有序的
（1）我们可以从子序列长度为 1 开始进行归并，即一个数据为一个子序列
（2）从而得到区间长度为 2 的子序列，并对其进行归并，又会得到区间长度为4的有序子序列
（3）通过一次次扩大有序子序列的长度，并对其进行归并，即可实现原序列的整体有序

2.2 源代码

#include 
#define size 10

void MergeSort(int *num, int len)
{
    int i, j, k;
    // 临时数组，用于归并子序列
    int sort[size];
    // 左区间的起点、终点下标
    int L_start = 0, L_end = 0;
    // 右区间的起点、终点下标
    int R_start = 0, R_end = 0;

    // 区间长度 i，两倍递增
    for (i = 1; i < len; i *= 2)
    {
        // 根据区间长度划分多个左右两个区间
        for (L_start = 0; L_start < len - i; L_start = R_end + 1)
        {
            // 确定左右两个区间各自的起点、终点下标
            L_end = L_start + i - 1;
            R_start = L_end + 1;
            R_end = R_start + i - 1;
            
            // 右区间可能会超出数组长度
            if (R_end >= len)
            {
                R_end = len - 1;
            }

            // 临时数组下标
            j = 0;
            // 按大小顺序收集左右两个区间子序列的数据到临时数组中
            while (L_start <= L_end && R_start <= R_end)
            {
                // 比较左右区间内数据的大小
                if (num[L_start] < num[R_start])
                {
                    sort[j++] = num[L_start++];
                }
                else
                {
                    sort[j++] = num[R_start++];
                }
            }

            // 收集两个区间子序列中可能剩余的数据
            while (L_start <= L_end)
            {
                sort[j++] = num[L_start++];
            }
            while (R_start <= R_end)
            {
                sort[j++] = num[R_start++];
            }

            // 最后将排序好的数据重新录入原数组中
            while (j > 0)
            {
                num[--R_start] = sort[--j];
            }
        }
    } 
}

int main()
{
    int i, num[size] = {5, 3, 7, 1, 9, 2, 0, 4, 8, 6};
    MergeSort(num, size);
    
    for ( i = 0; i < size; i++)
    {
        printf("%d ", num[i]);
    }
    printf("\n");
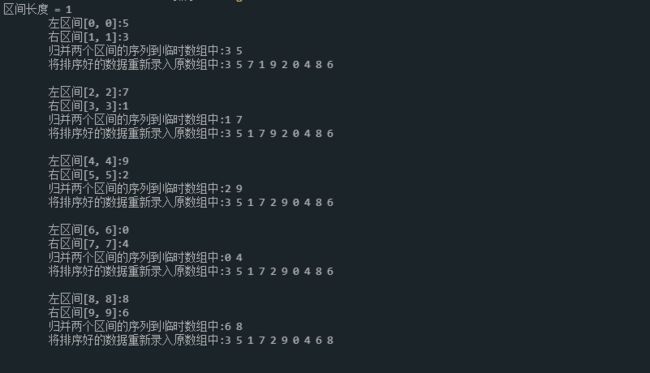
    return 0;
}

2.3 测试结果

3. 归并排序—递归

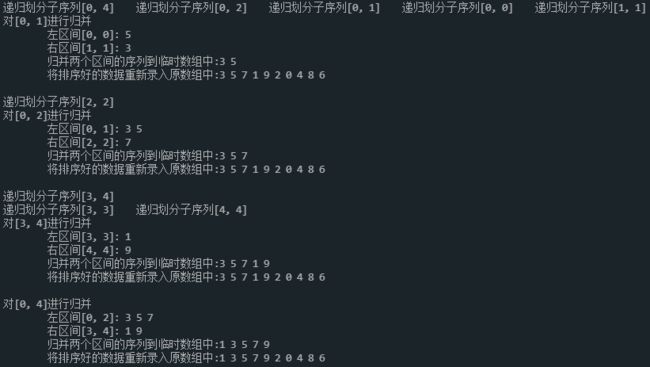
3.1 图文解析

归并排序的递归实现主要在于递归分治，对于递归算法，我们可以用二叉树的结构来理解
对于一个序列，递归划分左右两个子序列，函数递归到最深处时，一个数据即为一个子序列
然后利用递归回调的特性，对所有子序列进行归并排序，即可完成整个序列的排序

3.2 源代码

#include 
#define size 10

void Merge(int *num, int *sort, int low, int mid, int high)
{
    // 左区间起点下标
    int i = low;
    // 右区间起点下标
    int j = mid + 1;
    // 临时数组初始化下标
    int k = low;
    // 按大小顺序收集左右两个区间的数据到临时数组中
    while (i <= mid && j <= high)
    {
        if (num[i] < num[j])
        {
            sort[k++] = num[i++];
        }
        else
        {
            sort[k++] = num[j++];
        }
    }
    // 收集两个子序列中可能剩余的数据
    while (i <= mid)
    {
        sort[k++] = num[i++];
    }
    while (j <= high)
    {
        sort[k++] = num[j++];
    }    
    // 最后将收集好的数据重新录入原数组中
    while (k > 0)
    {
        num[--j] = sort[--k];
    }
    
}

void MergeSort(int *num, int *sort, int low, int high)
{
    if (low < high)
    {
        int mid = (low + high) / 2;
        // 划分左子序列
        MergeSort(num, sort, low, mid);
        // 划分右子序列
        MergeSort(num, sort, mid + 1, high);
        // 在完成划分后进行归并
        Merge(num, sort, low, mid, high);
    }
    
}

int main()
{
    int i, sort[size], num[size] = {5, 3, 7, 1, 9, 2, 0, 4, 8, 6};
    MergeSort(num, sort, 0, size - 1);
    
    for (i = 0; i < size; i++)
    {
        printf("%d ", num[i]);
    }
    printf("\n");
    return 0;
}

3.3 测试结果