Codeforces Round 886 (Div. 4)

A. To My Critics

题目

题目链接

题意

给你三个数，请你判断这里面存在任意两个数的和不小于10

题解

输入之后三个数两两相加判断即可

代码

#include
using namespace std;
#define debug(x) cout<<#x<<" = "<<x<<endl

int main()
{
    long long t;
    cin>>t;
    for(int i=0;i<t-1;++i)
    {
        int a,b,c;
        cin>>a>>b>>c;
        if(((a+b)>=10)||((a+c)>=10)||((b+c)>=10))
            cout<<"YES\n";
        else cout<<"NO\n";
    }
            int a,b,c;
        cin>>a>>b>>c;
        if(((a+b)>=10)||((a+c)>=10)||((b+c)>=10))
            cout<<"YES";
        else cout<<"NO";
    return 0;
}

B. Ten Words of Wisdom

题目

题目链接

题意

给你$n$行数据，每一行有两个数，在第一个数不超过$10$的情况下，找到第二位最大的位置。

题解

输入的时候简单判断，用一个变量进行存储最大值一个变量存储最大值的位置，如果第一个数字大于$10$的话，后面的数字与最大值进行比较，如果后面的数字更大就更新坐标以及最大数字

代码

#include
using namespace std;
#define debug(x) cout<<#x<<" = "<<x<<endl

int main()
{
    long long t;
    cin>>t;
    while(t--)
    {
        int n;
        cin>>n;
        int maxzhi=INT_MIN;
        int shuru1,shuru2;
        int ans=1;
        for(int i=0;i<n;++i)
        {
            scanf("%d%d",&shuru1,&shuru2);
            if(shuru1<=10)
            {
                if(shuru2>maxzhi)
                {
                    maxzhi=shuru2;
                    ans=i+1;
                }
            }
        }
        cout<<ans<<endl;
    }
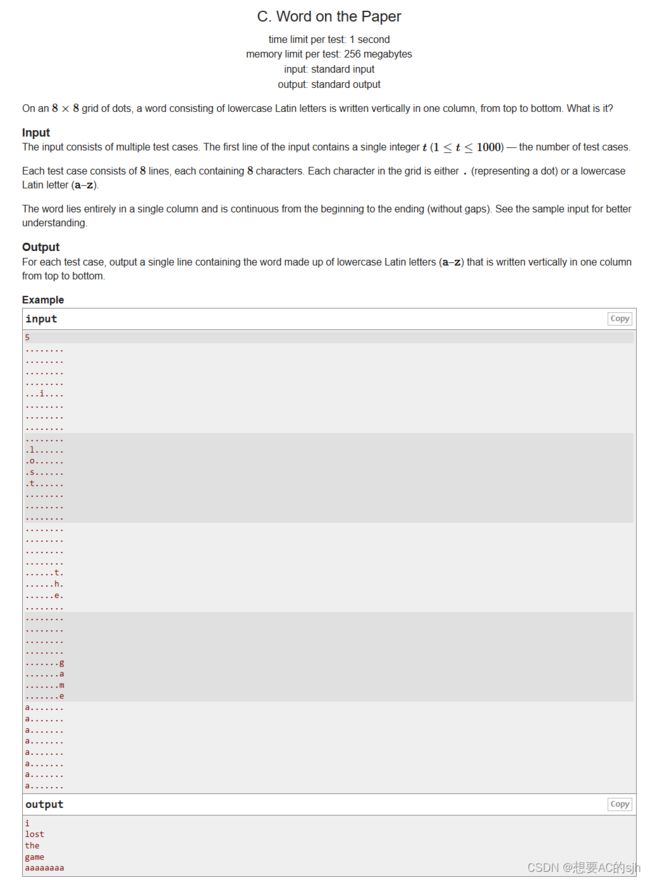
    return 0;
}

C. Word on the Paper

题目

题目链接

题意

给你一个矩阵，里面有"."以及一些字母，按照顺序提取出这些字母

题解

输入之后按层遍历数组，如果不是"."就直接输出就可以了

代码

#include
using namespace std;
#define debug(x) cout<<#x<<" = "<<x<<endl

int main()
{
    long long t;
    cin>>t;
    while(t--)
    {
        string s[8];
        for(int j=0;j<8;++j)
        {
            cin>>s[j];
        }
        for(int j=0;j<8;++j)
        {
            for(int i=0;i<s[j].size();++i)
            {
                if(s[j][i]!='.')cout<<s[j][i];
            }
        }
        cout<<endl;
    }
    return 0;
}

D. Balanced Round

题目

题目链接

题意

给你一个数组，对数组进进行删除数字操作再进行排序，要求排序之后的数组相邻两个数字的差不超过$k$，求删除的个数最少是多少

题解

输入之后对整个数组进行排序，求最大连续区间

代码

#include
using namespace std;
#define int long long

const int N = 2e5+10;
long long a[N]{0};

int cmp(int a,int b)
{
    return a<b;
}

inline int fastReadInt() {
    int x = 0;
    bool neg = false;
    char c = getchar();
    while (c < '0' || c > '9') {
        if (c == '-') neg = true;
        c = getchar();
    }
    while (c >= '0' && c <= '9') {
        x = (x * 10) + (c - '0');
        c = getchar();
    }
    return neg ? -x : x;
}

signed main()
{
    long long t;
    scanf("%lld",&t);
    while(t--)
    {
        long long n,k;
        n=fastReadInt();
        k=fastReadInt();
        for(int i=0;i<n;++i)
            a[i]=fastReadInt();
        sort(a,a+n,cmp);
        if(a[0]+k>a[n-1])
        {
            cout<<"0\n";
            continue;
        }
        int geshu=1;
        int maxzhi=1;
        for(int i=1;i<n;++i)
        {
            if(a[i]<=(a[i-1]+k))
            {
                geshu++;
                maxzhi=max(maxzhi,geshu);
            }
            else
            {
                maxzhi=max(maxzhi,geshu);
                geshu=1;
            }
        }
        printf("%lld\n",n-maxzhi);
    }
    return 0;
}

代码备注

空间大小一定要看清楚，数组开小了，结果一直超时

E. Cardboard for Pictures

题目

题目链接

题意

给你一组正方形，以及目标面积$c$，求每一个正方形的边长要向两边扩大多少才能够使得这些正方形的面积之和刚好等于$c$。

题解

由题目所给出的示意图可以看到，无论怎么增长这些正方形本身都有一定的面积，增长的部分可以分为两个部分，每一个正方形增长的部分都可以划分成四个小正方形和四个长方形分开来计算然后二分增长的长度即可

代码

#include
using namespace std;
#define int long long

const int N = 1e5+10;
long long a[N]{0};

int cmp(int a,int b)
{
    return a<b;
}

signed main()
{
    long long t;
    scanf("%lld",&t);
    while(t--)
    {
        long long n,c;
        scanf("%lld%lld",&n,&c);
        long long ans=0;
        long long shuru;
        long long bian=0;
        for(int i=0;i<n;++i)
        {
            scanf("%lld",&shuru);
            ans+=shuru*shuru;
            bian+=shuru;
        }
        __int128 left=1,right=1e9+10;
        c-=ans;
        while(left<right)
        {
            __int128 mid=(left+right)>>1;
            if((mid*mid*4*n)<(__int128)c-mid*4*bian)left=mid+1;
            else right=mid;
        }
        printf("%lld\n",(long long)left);
    }
    return 0;
}

代码备注

注意这一道题使用long long也会超过范围，要使用__int128