leetcode-二分查找
目录
704. Binary Search
35. Search Insert Position
在无序数组中使用二分
162. Find Peak Element
在二维数组中使用二分
74. Search a 2D Matrix
在有序数组中使用二分
二分查找实际上可以理解为数组上的双指针技巧的使用:左右指针夹逼,相遇停止。
167. Two Sum II - Input Array Is Sorted
(1) Two Sum II - Input Array Is Sorted - LeetCode
初始思路:
穷举第一个元素first,让first指针从起始开始固定,往前穷举n躺,每趟往前找第一个元素second。
每趟的查找可优化为二分查找。
故time complecxity为O(nlogn)
class Solution {
public:
vector twoSum(vector& numbers, int target) {
vector res;
int n = numbers.size();
//耗费O(nlogn)
for(int first=0;firsttarget){//往左走
hi = mid - 1;
}
}
}
return res;
}
}; 思路二:双指针夹逼,相遇停止
class Solution {
public:
vector twoSum(vector& numbers, int target) {
vector res;
int n = numbers.size();
int left = 0;
int right = n-1;
while(left < right){
if((numbers[left]+numbers[right])==target){
res.push_back(left+1);
res.push_back(right+1);
return res;
}
else if((numbers[left]+numbers[right])target){
right--;
}
}
return res;
}
}; 这是数组的双指针技巧,left和right指针根据条件前进一步,最终两指针相遇则数组遍历完毕。
在二分查找中,lo相当于双指针的left,hi相当于双指针的right,与前面双指针技巧不同的是:lo(left)和hi(right)根据条件前进k/2,最终相遇的速度更快。
704. Binary Search
(1) Binary Search - LeetCode
迭代方式
int search(vector& nums, int target) {
int lo = 0;
int hi = nums.size()-1;
while(lo<=hi){
int mid = (lo+hi)/2;
if(nums[mid] == target)
return mid;
else if(target < nums[mid]){
hi = mid-1;
}
else{
lo = mid + 1;
}
}
return -1;
} 转为递归
int search(vector& nums, int target) {
return helper(nums,0,nums.size()-1,target);
}
int helper(vector& nums, int lo,int hi,int target){
if(lo>hi) return -1;
int mid = (lo+hi)/2;
if(nums[mid]==target){
return mid;
}
else if(target < nums[mid]){
return helper(nums,lo,mid-1,target);
}
else{
return helper(nums,mid+1,hi,target);
}
} 上述为简单的二分查找算法,使用条件
如果允许重复?
二分是否一定要求有序数组?
35. Search Insert Position
(1) Search Insert Position - LeetCode
迭代思路:
int searchInsert(vector& nums, int target) {
int lo = 0;
int hi = nums.size()-1;
while(lo<=hi){
int mid = (lo + hi)/2;
if(nums[mid]==target){
return mid;
}
else if(target 递归:
int searchInsert(vector& nums, int target) {
return helper(nums,0,nums.size()-1,target);
}
int helper(vector& nums,int lo,int hi,int target){
if(lo>hi) return lo;
int mid = (lo+hi)/2;
if(nums[mid]==target){
return mid;
}
else if(target 在有序数组中通常可以考虑二分查找
在无序数组中使用二分
构造顺序性
287. Find the Duplicate Number
(3) Find the Duplicate Number - LeetCode
由于只有n+1个元素,且给定了范围1-n,所以要从position思考——位置的顺序
使用二分查找:
class Solution {
public:
int findDuplicate(vector& nums) {
int n = nums.size();
int begin = 0;
int end = n - 1;
while(begin < end){
int count = 0;
int mid = (begin+end) / 2;
//线性统计≤nums[mid]的数目
for(int i=0; i
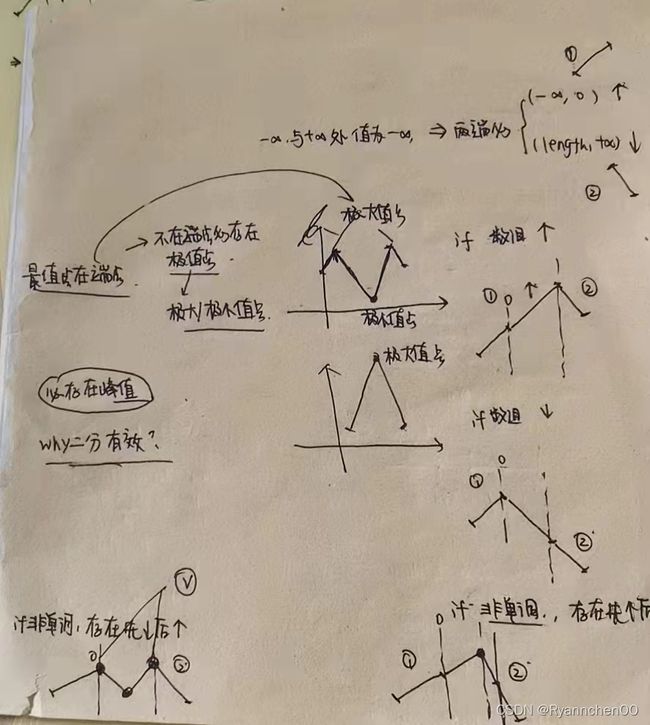
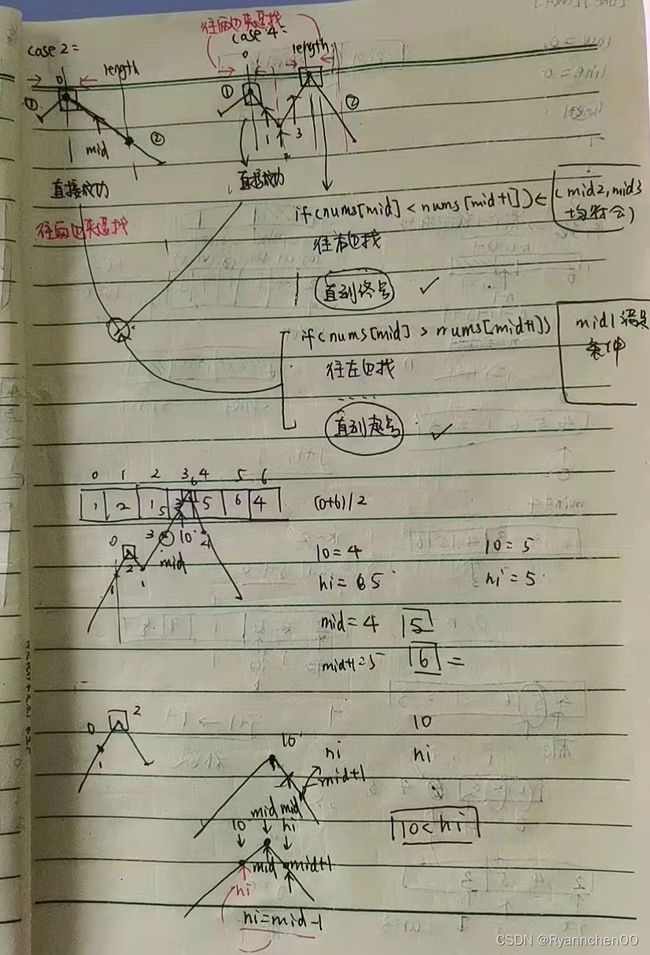
162. Find Peak Element
(1) Find Peak Element - LeetCode
不知道正确与否的思考过程:
使用二分的思路:
int findPeakElement(vector& nums) {
int lo = 0;
int hi = nums.size()-1;
while(lo<=hi){
int mid = (lo+hi)/2;
if(mid==(nums.size()-1)) return mid;
if(nums[mid]nums[mid+1]){
hi = mid -1;
}
}
return lo;
} 在二维数组中使用二分
74. Search a 2D Matrix
(1) Search a 2D Matrix - LeetCode
初始思路:
基于索引查找的思路:先按行二分圈定在哪一行,再在确定的行内二分。
时间复杂度:O(logM + logN)
bool searchMatrix(vector>& matrix, int target) {
int col_lo = 0;
int col_hi = matrix.size()-1;
int row_lo = 0;
int row_hi = matrix[0].size()-1;
while(col_lo <= col_hi){
int col_mid = (col_lo+col_hi)/2;
if(matrix[col_mid][0]==target){
return true;
}
else if(target < matrix[col_mid][0]){//往上找
col_hi = col_mid-1;
}
else if(target > matrix[col_mid][0]){//往下找
col_lo = col_mid+1;
}
}//找到target可能所在的行
if(col_hi>=0){
while(row_lo<=row_hi){
int mid = (row_lo+row_hi)/2;
if(matrix[col_hi][mid]==target){
return true;
}
else if(target < matrix[col_hi][mid]){
row_hi = mid - 1;
}
else{
row_lo = mid + 1;
}
}
}
return false;
} 把二维数组拉平进行一维的二分:
时间复杂度:O log(M*N)
bool searchMatrix(vector>& matrix, int target) {
int lo = 0;
int col = matrix[0].size();
int row = matrix.size();
int hi = row * col - 1;
while(lo <= hi){
int mid = (lo+hi)/2;
int mid_row = mid / col;
int mid_col = mid % col;
if(target == matrix[mid_row][mid_col]){
return true;
}
else if(target < matrix[mid_row][mid_col]){
hi = mid - 1;
}
else{
lo = mid + 1;
}
}
return false;
} 以下给出了第三个思路:
【宫水三叶】一题双解:「二分」&「抽象 BST」解法 - 搜索二维矩阵 - 力扣(LeetCode) (leetcode-cn.com)
以第一行的最右元素为根,行为方向向前走为左儿子,列为方向向下走为右儿子。
抽象了BST问题进行查找
bool searchMatrix(vector>& matrix, int target) {
int row = matrix.size();
int col = matrix[0].size();
int j = col-1;
int i = 0;
while(j>=0 && i