【直线平移/数控技术】二维线段平移特定距离
文章目录
- 一、往线段方向的左边平移特定距离
- 二、往线段方向的右边平移特定距离
一、往线段方向的左边平移特定距离
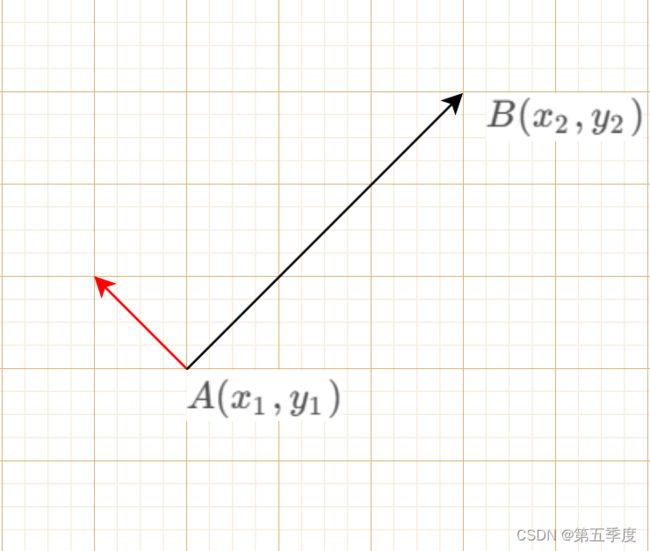
假设有一条线段AB的起点坐标为 A ( x 1 , y 1 ) A(x_1,y_1) A(x1,y1),终点坐标为 B ( x 2 , y 2 ) B(x_2,y_2) B(x2,y2),这条线段所表示的矢量为 A B ⃗ = ( x 2 − x 1 , y 2 − y 1 ) \vec{AB}=(x_2-x_1,y_2-y_1) AB=(x2−x1,y2−y1)。我们现在要将该矢量往它的方向的左边平移距离 d d d,并且获得平移之后的线段起点坐标 A ′ ( x 1 ′ , y 1 ′ ) A'(x_1',y_1') A′(x1′,y1′)和终点坐标 B ′ ( x 2 ′ , y 2 ′ ) B'(x_2',y_2') B′(x2′,y2′)。如图所示。

第一步,求出 A B ⃗ \vec{AB} AB的单位向量,将该单位向量使用逆时针旋转矩阵进行旋转90度。如图所示,红色向量为 A B ⃗ \vec{AB} AB的单位向量逆时针旋转90度得到的向量。
求出向量AB的单位向量:
e ⃗ = A B ⃗ ∣ A B ⃗ ∣ \vec{e}=\frac{\vec{AB}}{|\vec{AB}|} e=∣AB∣AB逆时针旋转矩阵表示如下:
R = [ 0 1 − 1 0 ] R=\left[\begin{matrix}0&1\\-1&0\end{matrix}\right] R=[0−110]使用逆时针旋转矩阵对单位向量进行旋转得到旋转之后的单位向量:
e ′ ⃗ = e ⃗ × R \vec{e'}=\vec{e}\times R e′=e×R
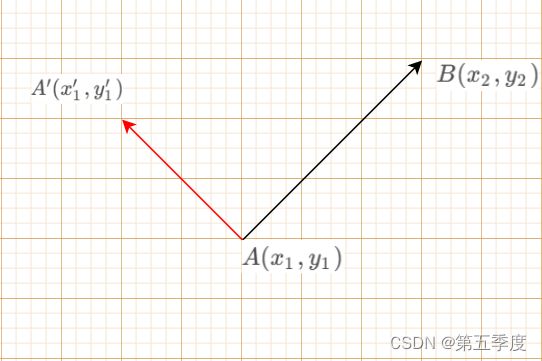
第二步,将旋转之后的单位向量 e ′ ⃗ \vec{e'} e′乘以平移距离 d d d,获得向量 A A ′ ⃗ \vec{AA'} AA′, A A A点坐标实际上表示的是向量 O A ⃗ \vec{OA} OA,由于 O A ′ ⃗ = O A ⃗ + A A ′ ⃗ \vec{OA'}=\vec{OA}+\vec{AA'} OA′=OA+AA′,所以向量 O A ′ ⃗ \vec{OA'} OA′可知,即获得了 A ′ A' A′的坐标。如图所示。
将旋转之后的单位向量 e ′ ⃗ \vec{e'} e′乘以平移距离 d d d,获得向量 A A ′ ⃗ \vec{AA'} AA′:
A A ′ ⃗ = d e ′ ⃗ = d e ⃗ × R \vec{AA'}=d\vec{e'}=d \vec{e}\times R AA′=de′=de×R得到向量 O A ′ ⃗ \vec{OA'} OA′, O A ′ ⃗ \vec{OA'} OA′即 A ′ A' A′点的坐标:
O A ′ ⃗ = O A ⃗ + A A ′ ⃗ = ( x 1 , y 1 ) + d e ⃗ × R \vec{OA'}=\vec{OA}+\vec{AA'}=(x_1,y_1)+d\vec{e}\times R OA′=OA+AA′=(x1,y1)+de×R
第三步,利用 A ′ B ′ ⃗ = A B ⃗ \vec{A'B'}=\vec{AB} A′B′=AB,由 O B ′ ⃗ = O A ′ ⃗ + A ′ B ′ ⃗ \vec{OB'}=\vec{OA'}+\vec{A'B'} OB′=OA′+A′B′得到 B ′ B' B′点的坐标,如图所示。
利用 A ′ B ′ ⃗ = A B ⃗ \vec{A'B'}=\vec{AB} A′B′=AB,由 O B ′ ⃗ = O A ′ ⃗ + A ′ B ′ ⃗ \vec{OB'}=\vec{OA'}+\vec{A'B'} OB′=OA′+A′B′得到 B ′ B' B′点的坐标:
O B ′ ⃗ = O A ′ ⃗ + A B ⃗ = ( x 1 , y 1 ) + d e ⃗ × R + ( x 2 − x 1 , y 2 − y 1 ) = ( x 2 , y 2 ) + d e ⃗ × R \vec{OB'}=\vec{OA'}+\vec{AB}=(x_1,y_1)+d\vec{e}\times R+(x_2-x_1,y_2-y_1)=(x_2,y_2)+d\vec{e}\times R OB′=OA′+AB=(x1,y1)+de×R+(x2−x1,y2−y1)=(x2,y2)+de×R
综上,我们得到了两条式子用来求AB向左边平移特定距离d之后得到的线段起点和终点坐标。分别如下:
O A ′ ⃗ = ( x 1 , y 1 ) + d e ⃗ × R O B ′ ⃗ = ( x 2 , y 2 ) + d e ⃗ × R \vec{OA'}=(x_1,y_1)+d\vec{e}\times R\\\vec{OB'}=(x_2,y_2)+d\vec{e}\times R OA′=(x1,y1)+de×ROB′=(x2,y2)+de×R其中, ( x 1 , y 1 ) (x_1,y_1) (x1,y1)为点A的坐标(已知), ( x 2 , y 2 ) (x_2,y_2) (x2,y2)为点B的坐标(已知), d d d是平移的距离(已知), R R R是逆时针旋转矩阵(已知), e ⃗ \vec{e} e是 A B ⃗ \vec{AB} AB的单位向量(可求),将这些已知量和可求量代入上面两条式子,可以得到求点 A ′ A' A′ 和点 B ′ B' B′ 的两条公式:
A ′ = O A ′ ⃗ = ( d ( y 1 − y 2 ) ( x 2 − x 1 ) 2 + ( y 2 − y 1 ) 2 + x 1 , d ( x 2 − x 1 ) ( x 2 − x 1 ) 2 + ( y 2 − y 1 ) 2 + y 1 ) B ′ = O B ′ ⃗ = ( d ( y 1 − y 2 ) ( x 2 − x 1 ) 2 + ( y 2 − y 1 ) 2 + x 2 , d ( x 2 − x 1 ) ( x 2 − x 1 ) 2 + ( y 2 − y 1 ) 2 + y 2 ) A'=\vec{OA'}=(\frac{d(y_1-y_2)}{\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}}+x_1,\frac{d(x_2-x_1)}{\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}}+y_1)\\B'=\vec{OB'}=(\frac{d(y_1-y_2)}{\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}}+x_2,\frac{d(x_2-x_1)}{\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}}+y_2) A′=OA′=((x2−x1)2+(y2−y1)2d(y1−y2)+x1,(x2−x1)2+(y2−y1)2d(x2−x1)+y1)B′=OB′=((x2−x1)2+(y2−y1)2d(y1−y2)+x2,(x2−x1)2+(y2−y1)2d(x2−x1)+y2)
二、往线段方向的右边平移特定距离
跟左平移的推理类似,但是逆时针旋转矩阵需要替换为顺时针旋转矩阵:
R = [ 0 − 1 1 0 ] R=\left[\begin{matrix}0&-1\\1&0\end{matrix}\right] R=[01−10]
最后,推导出的公式如下:
A ′ = O A ′ ⃗ = ( d ( y 2 − y 1 ) ( x 2 − x 1 ) 2 + ( y 2 − y 1 ) 2 + x 1 , d ( x 1 − x 2 ) ( x 2 − x 1 ) 2 + ( y 2 − y 1 ) 2 + y 1 ) B ′ = O B ′ ⃗ = ( d ( y 2 − y 1 ) ( x 2 − x 1 ) 2 + ( y 2 − y 1 ) 2 + x 2 , d ( x 1 − x 2 ) ( x 2 − x 1 ) 2 + ( y 2 − y 1 ) 2 + y 2 ) A'=\vec{OA'}=(\frac{d(y_2-y_1)}{\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}}+x_1,\frac{d(x_1-x_2)}{\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}}+y_1)\\B'=\vec{OB'}=(\frac{d(y_2-y_1)}{\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}}+x_2,\frac{d(x_1-x_2)}{\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}}+y_2) A′=OA′=((x2−x1)2+(y2−y1)2d(y2−y1)+x1,(x2−x1)2+(y2−y1)2d(x1−x2)+y1)B′=OB′=((x2−x1)2+(y2−y1)2d(y2−y1)+x2,(x2−x1)2+(y2−y1)2d(x1−x2)+y2)