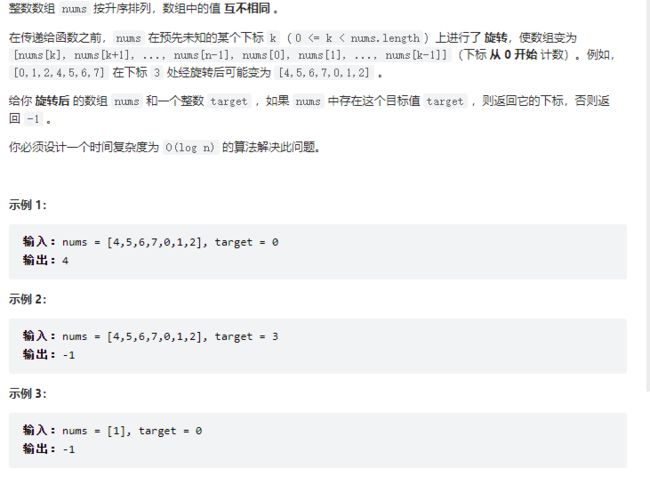
leetcode:33. 搜索旋转排序数组
题目来源
- leetcode:33. 搜索旋转排序数组
题目描述
class Solution {
public:
int search(vector<int>& nums, int target) {
}
};
题目解析
思路
- 因为是有序数组,所以我们应该去二分
- 但是这里是一个原本有序的数组在某个点上进行了旋转,也就会将一段原本升序的数组分成了两段
- 可以先使用二分法找到旋转点,再使用二分法在两个数组中分别寻找target。
class Solution {
int find(vector<int>& nums, int l, int r, int target){
while (l <= r){
int mid = l + (r - l) / 2;
if(nums[mid] == target){
return mid;
}else if(nums[mid] < target){
l = mid + 1;
}else{
r = mid - 1;
}
}
return -1;
}
public:
int search(vector<int>& nums, int target) {
int n = nums.size();
int idx = 0;
for (int i = 0; i < n - 1; ++i) {
if(nums[i] > nums[i + 1]){
idx = i;
break;
}
}
int ans = find(nums, 0, idx, target);
if(ans != -1 && idx + 1 < n){
ans = find(nums, idx + 1, n - 1, target);
}
return ans;
}
};
二分解法
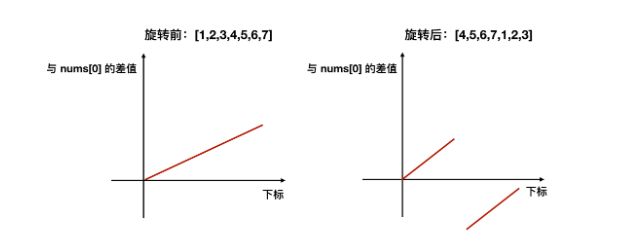
二分的本质是两段性,只要某一段满足某个性质,另一段不满足某个性质,就可以用[二分]
经过旋转的数组,显然前半段满足>= nums[0],而后半段不满足 >= nums[0]。我们可以以此作为依据,通过「二分」找到旋转点。
找到旋转点之后,再通过比较 target 和 nums[0] 的大小,确定 target 落在旋转点的左边还是右边。
class Solution {
public:
int search(vector<int>& nums, int target) {
int n = nums.size();
if(n == 0){
return -1;
}
if(n == 1){
return nums[0] == target ? 0 : -1;
}
// 第一次「二分」:从中间开始找,找到满足 >=nums[0] 的分割点(旋转点)
int l = 0, r = n - 1;
while (l < r){
int mid = (l + r) / 2;
if(nums[mid] >= nums[0]){
l = mid;
}else{
r = mid - 1;
}
}
// 第二次「二分」:通过和 nums[0] 进行比较,得知 target 是在旋转点的左边还是右边
if(target >= nums[0]){
l = 0;
}else{
l = l + 1;
r = n - 1;
}
while(l < r){
int mid = (l + r) >> 1;
if(nums[mid] >= target){
r = mid;
}
else l = mid + 1;
}
return (nums[r] == target ? r : -1);
}
};
思路一
对于旋转数组,nums = [4,5,6,7,0,1,2]
- 首先根据nums[0]与target的关系判断target是在左段还是右段
- 例如 target = 5, 目标值在左半段,因此在 [4, 5, 6, 7, inf, inf, inf] 这个有序数组里找就行了;
- 例如 target = 1, 目标值在右半段,因此在 [-inf, -inf, -inf, -inf, 0, 1, 2] 这个有序数组里找就行了。
- 如此,我们又双叒叕将「旋转数组中找目标值」 转化成了 「有序数组中找目标值」
class Solution {
public:
int search(vector<int>& nums, int target) {
int lo = 0, hi = nums.size() - 1l;
while (lo <= hi){
int mid = lo + (hi - lo) / 2;
if(nums[mid] == target){
return mid;
}
// 先根据 nums[0] 与 target 的关系判断目标值是在左半段还是右半段
if(target >= nums[0]){
// 目标值在左半段时,若 mid 在右半段,则将 mid 索引的值改成 inf
if (nums[mid] < nums[0]) {
nums[mid] = INT32_MAX;
}
}else{
// 目标值在右半段时,若 mid 在左半段,则将 mid 索引的值改成 -inf
// 目标值在右半段时,若 mid 在左半段,则将 mid 索引的值改成 -inf
if (nums[mid] >= nums[0]) {
nums[mid] = INT32_MIN;
}
}
if(nums[mid] < target){
lo = mid + 1;
}else{
hi = mid - 1;
}
}
return -1;
}
};
思路二:
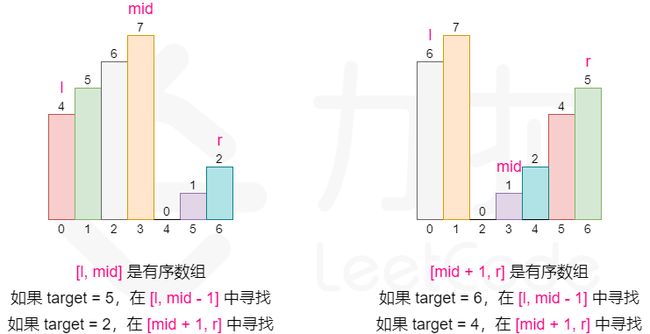
- 将数组一分为二,其中一个一定是有序的,另一个可能是有序的,也可能是部分有序的。此时有序部分用二分法查找。其中一个一定有序,另一个可能有序,可能无序。就这样循环.
class Solution {
public:
int search(vector<int>& nums, int target) {
int l = 0, r = nums.size() - 1l;
while (l <= r){
int mid = l + (r - l) / 2;
if(nums[mid] == target){
return mid;
}
if(nums[l] <= nums[mid]){ //mid左侧为有序数组
if(nums[l] <= target && target < nums[mid]){//如果target在mid左侧的话
r = mid - 1;
}else{//在mid右侧
l = mid + 1;
}
}else{ //mid右侧为有序数组
if(nums[mid] < target && target <= nums[r]){//如果target在mid右侧的话
l = mid + 1;
}else{//在mid左侧
l = mid - 1;
}
// 为什么只在target与nums[l]或nums[r]比较的时候取等,而不在其他位置取等?
// 因为另一边的 nums[mid] == target 是否相等 已经在上面的 if 分支里判断了
}
}
return -1;
}
};
思路
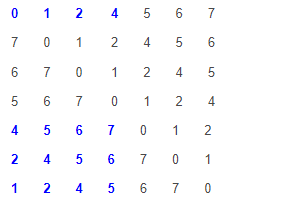
对于数组 [0 1 2 4 5 6 7] 共有下列七种旋转方法(红色表示中点之前或者之后一定为有序的):
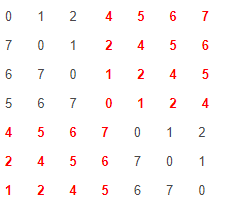
二分搜索法的关键在于获得了中间数之后,判断下面要搜索左半段还是右半段,观察上面红色的数字都是升序的,可以得出规律,如果nums[mid] < nums[right] ,则右半段是有序的;如果nums[mid] > nums[right],则左半段是有序的。我们只要在有序的半段里用首尾两个数组来判断目标值是否在这一区域内,这样就可以确定保留哪半边了
class Solution {
public:
int search(vector<int>& nums, int target) {
int left = 0, right = nums.size() - 1;
while (left < right){
int mid = left + (right - left) / 2;
if(nums[target] == target){
return mid;
}
if(nums[mid] < nums[target]){
// a b c e d f
if(nums[mid] < target && nums[right] >= target){
left = mid + 1;
}else{
right = mid - 1;
}
}else{
if(nums[left] <= target && nums[mid] > target){
right = mid - 1;
}else{
left = mid + 1;
}
}
}
return -1;
}
};
为啥非得用中间的数字跟最右边的比较呢?难道跟最左边的数字比较不行吗,当中间的数字大于最左边的数字时,左半段也是有序的啊
貌似也可以做,但是有一个问题,那就是在二分搜索中,nums[mid] 和 nums[left] 还有可能相等的,当数组中只有两个数字的时候,比如 [3, 1],那该去取那一边呢?由于只有两个数字且 nums[mid] 不等于 target,target 只有可能在右半边出现。最好的方法就是让其无法进入左半段,就需要左半段是有序的,而且由于一定无法同时满足 nums[left] <= target && nums[mid] > target,因为 nums[left] 和 nums[mid] 相等,同一个数怎么可能同时大于等于 target,又小于 target。由于这个条件不满足,则直接进入右半段继续搜索即可,所以等于的情况要加到 nums[mid] > nums[left] 的情况中,变成大于等于,参见代码如下:
class Solution {
public:
int search(vector<int>& nums, int target) {
int left = 0, right = nums.size() - 1;
while (left <= right) {
int mid = left + (right - left) / 2;
if (nums[mid] == target) return mid;
if (nums[mid] >= nums[left]) {
if (nums[left] <= target && nums[mid] > target) right = mid - 1;
else left = mid + 1;
} else {
if (nums[mid] < target && nums[right] >= target) left = mid + 1;
else right = mid - 1;
}
}
return -1;
}
};
类似题目
| 题目 | 思路 |
|---|---|
| leetcode:33. 原本有序的数组(值互不相同)在某个点上进行了旋转,搜索这个旋转数组中target的下标 Search in Rotated Sorted Array | 如果nums[mid] < nums[right] ,则右半段是有序的;如果nums[mid] > nums[right],则左半段是有序的。们只要在有序的半段里用首尾两个数组来判断目标值是否在这一区域内,这样就可以确定保留哪半边了 |
| leetcode:81. 原本有序的数组(值可以相同)在某个点上进行了旋转,搜索这个旋转数组中target的下标 Search in Rotated Sorted Array II | 和33题目思路一样,只是nums[mid] == nums[right]时,right– |
| leetcode:153. 对一个有序数组进行了若干次旋转,让找出旋转数组的最小值 Find Minimum in Rotated Sorted Array | |
| leetcode:154. 寻找旋转排序数组中的最小值 II(含重复数字) Find Minimum in Rotated Sorted Array II |