二叉搜索树

目录

查找值为val的节点

插入值为val的节点

删除值为val的节点

性能分析

---

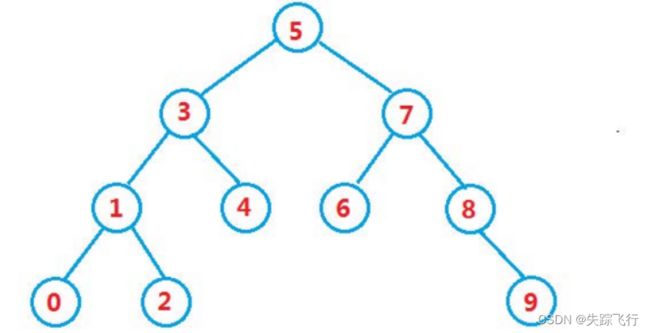
二叉搜索树又称二叉排序树,是一颗空树,或者是具有以下性质的二叉树:

        ●若他的左子树不为空,则左子树上所有节点的值都小于根节点的值

        ●若他的右子树不为空,则右子树上所有节点的值都大于根节点的值

        ●它的左右子树也分别为二叉搜索树

 首先先定义一颗二叉搜索树

---

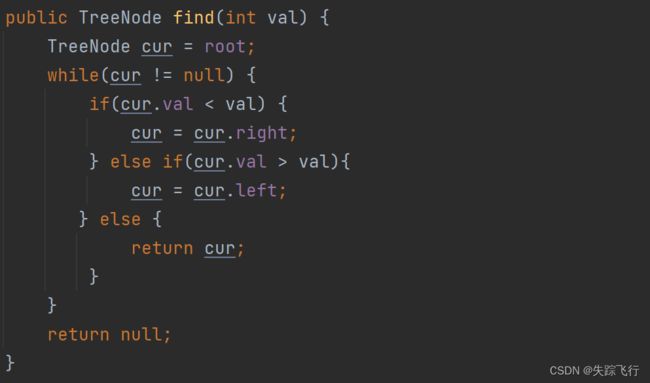
查找值为val的节点

根据二叉搜索树的性质,左子树的节点的值都小于根节点,右子树上的值都大于根节点,我们要查找一个数,只要比根节点大就去右子树找,否则去左子树上找,找到则返回这个节点,如果遍历整个左子树或者右子树都没有找到,则不存在这个节点,返回null

---

插入值为val的节点

当二叉搜索树为空的时候直接插入到根节点

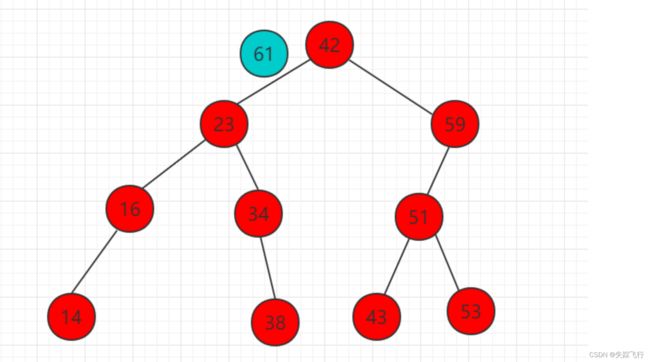
下图演示向二叉搜索树中插入61元素的步骤:

首先和根节点比较,61比42大,比较42右子树的根节点

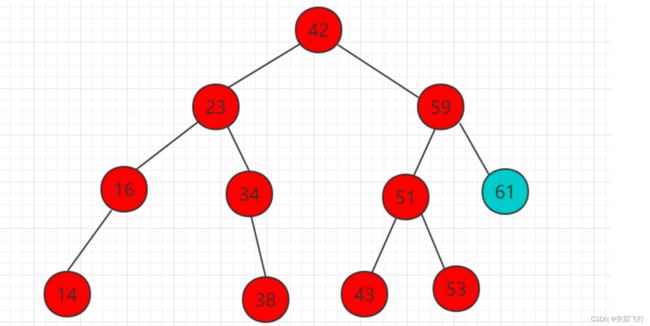
 61比59大,需要把61移动到59右子树的相应位置,而此时为空,直接插入作为59的右孩子.

把要插入的元素和根节点进行比较,比根节点大就去右子树比较,比根节点小就去左子树比较,,当树为空的时候,将待插入元素插入到叶子节点的位置.

代码实现:

public void insert(int val) {
        if (root == null) {
            root = new TreeNode(val);
            return;
        }
        TreeNode cur = root;
        TreeNode parent = null;
        while (cur != null) {
            if (cur.val < val) {
                parent = cur;
                cur = cur.right;
            } else if (cur.val == val) {
                 return; //相等的时候不用插入
            } else {
                parent = cur; 
                cur = cur.left;
            }
        }
        TreeNode node = new TreeNode(val);  //待插入节点
        if (parent.val < val) {
            parent.right = node;
        } else {
            parent.left = node;
        }
    }

---

删除值为val的节点

二叉搜索树删除某个节点是比较复杂的,设待删除节点是cur,待删除节点的双亲节点是parent.大致分为三种情况

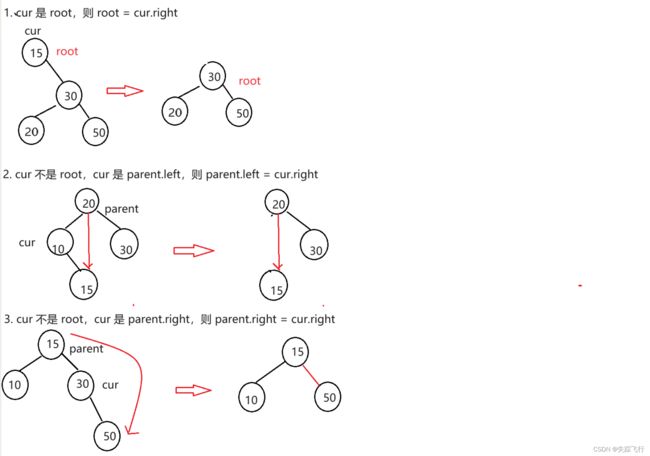
第一种情况:   cur.left == null 

直接让待删除节点的右孩子取代要删除节点的位置

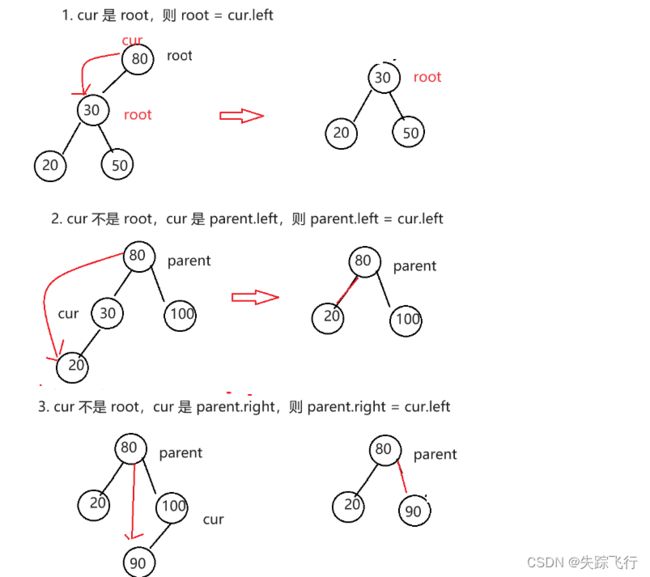
第二种情况: cur.right  ==  null

直接让待删除节点的左孩子取代要删除节点的位置

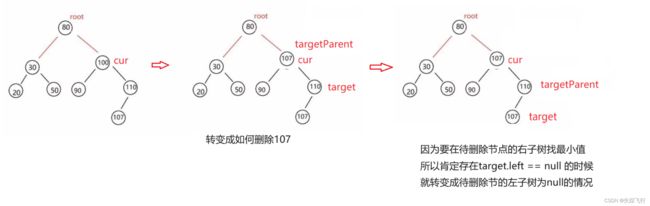
第三种情况:  待删除节点存在左孩子和有孩子

找到待删除节点右子树的最小值107,用107取代待删除节点的位置,然后删除原来的107节点

整体代码:

        public void remove(int val) {
            TreeNode cur = root;
            TreeNode parent = null;
            while (cur != null) {
                if(cur.val == val) { //找到了值为val的节点
                    removeNode(parent,cur);
                    return;
                } else if(cur.val < val) {
                    parent = cur;
                    cur = cur.right;
                } else {
                    parent = cur;
                    cur = cur.left;
                }
            }
        }

        private void removeNode(TreeNode parent, TreeNode cur) {
            if(cur.left == null) {
                if(cur == root) {
                    root = cur.right;
                } else if(cur == parent.left) {
                    parent.left = cur.right;
                } else {
                    // cur == parent.right 的情况
                    parent.right = cur.right;
                }
            } else if(cur.right == null) {
                if(cur == root) {
                    root = cur.left;
                } else if(cur == parent.left) {
                    parent.left = cur.left;
                } else {
                    //cur == parent.right的情况
                    parent.right = cur.left;
                }
            } else {
                TreeNode target = cur.right;
                TreeNode targetParent = cur;
                while(target.left != null) {
                    targetParent = target;
                    target = target.left;
                }
                cur.val = target.val;
                if(target == targetParent.left) {
                    targetParent.left = target.right;
                } else {
                    targetParent.right = target.right;
                }
            } 
        }

性能分析

通过上面查找和删除的代码可以看出插入和删除操作都要先查找相应的节点,说明查找效率代表了二叉搜索树各个操作的性能.

对于n个节点的二叉搜索树,若每个元素的查找效率相等,则二叉搜索树平均长度是节点在二叉搜索树的深度的函数,即节点越深,则比较次数越多 

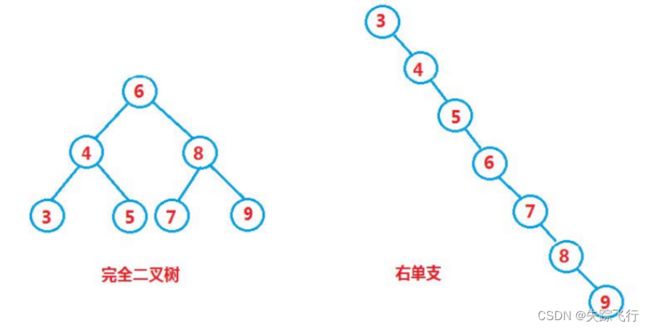
但对于同一个关键码集合,各个关键码插入的次序不同,可能得到不同的二叉搜索树:

最优情况下: 二叉搜索树是完全二叉树,平均比较次数为树的高度 log₂N

最差情况下: 二叉走所属是单分支树,平均比较次数 N / 2  时间复杂度是O(N)