【算法思想：回溯法】回溯算法入门级详解

回溯法是一种非常重要的算法思想，在大厂面试中频繁出现，所以做了一个笔记，记录了一下。

回溯算法与深度优先遍历

以下是维基百科中「回溯算法」和「深度优先遍历」的定义。

回溯法 采用试错的思想，它尝试分步的去解决一个问题。在分步解决问题的过程中，当它通过尝试发现现有的分步答案不能得到有效的正确的解答的时候，它将取消上一步甚至是上几步的计算，再通过其它的可能的分步解答再次尝试寻找问题的答案。回溯法通常用最简单的递归方法来实现，在反复重复上述的步骤后可能出现两种情况：

找到一个可能存在的正确的答案；
在尝试了所有可能的分步方法后宣告该问题没有答案。
深度优先搜索 算法（英语：Depth-First-Search，DFS）是一种用于遍历或搜索树或图的算法。这个算法会 尽可能深 的搜索树的分支。当结点 v 的所在边都己被探寻过，搜索将 回溯 到发现结点 v 的那条边的起始结点。这一过程一直进行到已发现从源结点可达的所有结点为止。如果还存在未被发现的结点，则选择其中一个作为源结点并重复以上过程，整个进程反复进行直到所有结点都被访问为止。

我刚开始学习「回溯算法」的时候觉得很抽象，一直不能理解为什么递归之后需要做和递归之前相同的逆向操作，在做了很多相关的问题以后，我发现其实「回溯算法」与「 深度优先遍历 」有着千丝万缕的联系。

个人理解

「回溯算法」与「深度优先遍历」都有「不撞南墙不回头」的意思。我个人的理解是：「回溯算法」强调了「深度优先遍历」思想的用途，用一个 不断变化 的变量，在尝试各种可能的过程中，搜索需要的结果。强调了 回退 操作对于搜索的合理性。而「深度优先遍历」强调一种遍历的思想，与之对应的遍历思想是「广度优先遍历」。至于广度优先遍历为什么没有成为强大的搜索算法，我们在题解后面会提。

搜索与遍历

我们每天使用的搜索引擎帮助我们在庞大的互联网上搜索信息。搜索引擎的「搜索」和「回溯搜索」算法里「搜索」的意思是一样的。

搜索问题的解，可以通过 遍历 实现。所以很多教程把「回溯算法」称为爆搜（暴力解法）。因此回溯算法用于 搜索一个问题的所有的解 ，通过深度优先遍历的思想实现。

与动态规划的区别

共同点

用于求解多阶段决策问题。多阶段决策问题即：

求解一个问题分为很多步骤（阶段）； 每一个步骤（阶段）可以有多种选择。

不同点

动态规划只需要求我们评估最优解是多少，最优解对应的具体解是什么并不要求。因此很适合应用于评估一个方案的效果； 回溯算法可以搜索得到所有的方案（当然包括最优解），但是本质上它是一种遍历算法，时间复杂度很高。

从全排列问题开始理解回溯算法

我们尝试在纸上写 33 个数字、44 个数字、55 个数字的全排列，相信不难找到这样的方法。以数组 [1, 2, 3] 的全排列为例。

• 先写以 11 开头的全排列，它们是：[1, 2, 3], [1, 3, 2]，即 1 + [2, 3] 的全排列（注意：递归结构体现在这里）；
• 再写以 22 开头的全排列，它们是：[2, 1, 3], [2, 3, 1]，即 2 + [1, 3] 的全排列；
• 最后写以 33 开头的全排列，它们是：[3, 1, 2], [3, 2, 1]，即 3 + [1, 2] 的全排列。

总结搜索的方法：按顺序枚举每一位可能出现的情况，已经选择的数字在 当前 要选择的数字中不能出现。按照这种策略搜索就能够做到 不重不漏。这样的思路，可以用一个树形结构表示。

看到这里的朋友，建议先尝试自己画出「全排列」问题的树形结构。

说明：

• 每一个结点表示了求解全排列问题的不同的阶段，这些阶段通过变量的「不同的值」体现，这些变量的不同的值，称之为「状态」；
• 使用深度优先遍历有「回头」的过程，在「回头」以后， 状态变量需要设置成为和先前一样 ，因此在回到上一层结点的过程中，需要撤销上一次的选择，这个操作称之为「状态重置」；
• 深度优先遍历，借助系统栈空间，保存所需要的状态变量，在编码中只需要注意遍历到相应的结点的时候，状态变量的值是正确的，具体的做法是：往下走一层的时候，path 变量在尾部追加，而往回走的时候，需要撤销上一次的选择，也是在尾部操作，因此 path 变量是一个栈；
• 深度优先遍历通过「回溯」操作，实现了全局使用一份状态变量的效果。

使用编程的方法得到全排列，就是在这样的一个树形结构中完成 遍历，从树的根结点到叶子结点形成的路径就是其中一个全排列。

设计状态变量

• 首先这棵树除了根结点和叶子结点以外，每一个结点做的事情其实是一样的，即：在已经选择了一些数的前提下，在剩下的还没有选择的数中，依次选择一个数，这显然是一个 递归 结构；
• 递归的终止条件是： 一个排列中的数字已经选够了 ，因此我们需要一个变量来表示当前程序递归到第几层，我们把这个变量叫做 depth，或者命名为 index ，表示当前要确定的是某个全排列中下标为 index 的那个数是多少；
• 布尔数组 used，初始化的时候都为 false 表示这些数还没有被选择，当我们选定一个数的时候，就将这个数组的相应位置设置为 true ，这样在考虑下一个位置的时候，就能够以 O(1)O(1) 的时间复杂度判断这个数是否被选择过，这是一种「以空间换时间」的思想。

这些变量称为「状态变量」，它们表示了在求解一个问题的时候所处的阶段。需要根据问题的场景设计合适的状态变量。

复杂度分析：（初学回溯算法的时候可以暂时跳过。）

回溯算法由于其遍历的特点，时间复杂度一般都比较高，有些问题分析起来很复杂。一些回溯算法解决的问题，剪枝剪得好的话，复杂度会降得很低，因此分析最坏时间复杂度的意义也不是很大。但还是视情况而定。

• 时间复杂度：

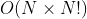
理解回溯

从 [1, 2, 3] 到 [1, 3, 2] ，深度优先遍历是这样做的，从 [1, 2, 3] 回到 [1, 2] 的时候，需要撤销刚刚已经选择的数 3，因为在这一层只有一个数 3 我们已经尝试过了，因此程序回到上一层，需要撤销对 2 的选择，好让后面的程序知道，选择 3 了以后还能够选择 2。

执行深度优先遍历，从较深层的结点返回到较浅层结点的时候，需要做「状态重置」，即「回到过去」、「恢复现场」，我们举一个例子。

通过打印输出观察

import java.util.ArrayDeque;
import java.util.ArrayList;
import java.util.Deque;
import java.util.List;


public class Solution {

    public List> permute(int[] nums) {
        int len = nums.length;
        // 使用一个动态数组保存所有可能的全排列
        List> res = new ArrayList<>();
        if (len == 0) {
            return res;
        }

        boolean[] used = new boolean[len];
        Deque path = new ArrayDeque<>(len);

        dfs(nums, len, 0, path, used, res);
        return res;
    }

    private void dfs(int[] nums, int len, int depth,
                     Deque path, boolean[] used,
                     List> res) {
        if (depth == len) {
            res.add(new ArrayList<>(path));
            return;
        }

        for (int i = 0; i < len; i++) {
            if (!used[i]) {
                path.addLast(nums[i]);
                used[i] = true;

                System.out.println("  递归之前 => " + path);
                dfs(nums, len, depth + 1, path, used, res);

                used[i] = false;
                path.removeLast();
                System.out.println("递归之后 => " + path);
            }
        }
    }

    public static void main(String[] args) {
        int[] nums = {1, 2, 3};
        Solution solution = new Solution();
        List> lists = solution.permute(nums);
        System.out.println(lists);
    }
}

控制台输出：

  递归之前 => [1]
  递归之前 => [1, 2]
  递归之前 => [1, 2, 3]
递归之后 => [1, 2]
递归之后 => [1]
  递归之前 => [1, 3]
  递归之前 => [1, 3, 2]
递归之后 => [1, 3]
递归之后 => [1]
递归之后 => []
  递归之前 => [2]
  递归之前 => [2, 1]
  递归之前 => [2, 1, 3]
递归之后 => [2, 1]
递归之后 => [2]
  递归之前 => [2, 3]
  递归之前 => [2, 3, 1]
递归之后 => [2, 3]
递归之后 => [2]
递归之后 => []
  递归之前 => [3]
  递归之前 => [3, 1]
  递归之前 => [3, 1, 2]
递归之后 => [3, 1]
递归之后 => [3]
  递归之前 => [3, 2]
  递归之前 => [3, 2, 1]
递归之后 => [3, 2]
递归之后 => [3]
递归之后 => []
输出 => [[1, 2, 3], [1, 3, 2], [2, 1, 3], [2, 3, 1], [3, 1, 2], [3, 2, 1]]

为什么不是广度优先遍历

• 首先是正确性，只有遍历状态空间，才能得到所有符合条件的解，这一点 BFS 和 DFS 其实都可以；
• 在深度优先遍历的时候，不同状态之间的切换很容易 ，可以再看一下上面有很多箭头的那张图，每两个状态之间的差别只有 11 处，因此回退非常方便，这样全局才能使用一份状态变量完成搜索；
• 如果使用广度优先遍历，从浅层转到深层，状态的变化就很大，此时我们不得不在每一个状态都新建变量去保存它，从性能来说是不划算的；
• 如果使用广度优先遍历就得使用队列，然后编写结点类。队列中需要存储每一步的状态信息，需要存储的数据很大，真正能用到的很少 。
• 使用深度优先遍历，直接使用了系统栈，系统栈帮助我们保存了每一个结点的状态信息。我们不用编写结点类，不必手动编写栈完成深度优先遍历。

不回溯可不可以

可以。搜索问题的状态空间一般很大，如果每一个状态都去创建新的变量，时间复杂度是 O(N)O(N)。在候选数比较多的时候，在非叶子结点上创建新的状态变量的性能消耗就很严重。

就本题而言，只需要叶子结点的那个状态，在叶子结点执行拷贝，时间复杂度是 O(N)O(N)。路径变量在深度优先遍历的时候，结点之间的转换只需要 O(1)O(1)。

最后，由于回溯算法的时间复杂度很高，因此在遍历的时候，如果能够提前知道这一条分支不能搜索到满意的结果，就可以提前结束，这一步操作称为 剪枝。

剪枝

• 回溯算法会应用「剪枝」技巧达到以加快搜索速度。有些时候，需要做一些预处理工作（例如排序）才能达到剪枝的目的。预处理工作虽然也消耗时间，但能够剪枝节约的时间更多；

提示：剪枝是一种技巧，通常需要根据不同问题场景采用不同的剪枝策略，需要在做题的过程中不断总结。

• 由于回溯问题本身时间复杂度就很高，所以能用空间换时间就尽量使用空间。

总结

做题的时候，建议 先画树形图 ，画图能帮助我们想清楚递归结构，想清楚如何剪枝。拿题目中的示例，想一想人是怎么做的，一般这样下来，这棵递归树都不难画出。

在画图的过程中思考清楚：

• 分支如何产生；
• 题目需要的解在哪里？是在叶子结点、还是在非叶子结点、还是在从跟结点到叶子结点的路径？
• 哪些搜索会产生不需要的解的？例如：产生重复是什么原因，如果在浅层就知道这个分支不能产生需要的结果，应该提前剪枝，剪枝的条件是什么，代码怎么写？

 

练习

下面提供一些我做过的「回溯」算法的问题，以便大家学习和理解「回溯」算法。

题型一：排列、组合、子集相关问题

提示：这部分练习可以帮助我们熟悉「回溯算法」的一些概念和通用的解题思路。解题的步骤是：先画图，再编码。去思考可以剪枝的条件， 为什么有的时候用 used 数组，有的时候设置搜索起点 begin 变量，理解状态变量设计的想法。

• 46. 全排列（中等）
• 47. 全排列 II（中等）：思考为什么造成了重复，如何在搜索之前就判断这一支会产生重复；
• 39. 组合总和（中等）
• 40. 组合总和 II（中等）
• 77. 组合（中等）
• 78. 子集（中等）
• 90. 子集 II（中等）：剪枝技巧同 47 题、39 题、40 题；
• 60. 第 k 个排列（中等）：利用了剪枝的思想，减去了大量枝叶，直接来到需要的叶子结点；
• 93. 复原 IP 地址（中等）

题型二：Flood Fill

提示：Flood 是「洪水」的意思，Flood Fill 直译是「泛洪填充」的意思，体现了洪水能够从一点开始，迅速填满当前位置附近的地势低的区域。类似的应用还有：PS 软件中的「点一下把这一片区域的颜色都替换掉」，扫雷游戏「点一下打开一大片没有雷的区域」。

下面这几个问题，思想不难，但是初学的时候代码很不容易写对，并且也很难调试。我们的建议是多写几遍，忘记了就再写一次，参考规范的编写实现（设置 visited 数组，设置方向数组，抽取私有方法），把代码写对。

• 733. 图像渲染（Flood Fill，中等）
• 200. 岛屿数量（中等）
• 130. 被围绕的区域（中等）
• 79. 单词搜索（中等）

说明：以上问题都不建议修改输入数据，设置 visited 数组是标准的做法。可能会遇到参数很多，是不是都可以写成成员变量的问题，面试中拿不准的记得问一下面试官

题型三：字符串中的回溯问题

提示：字符串的问题的特殊之处在于，字符串的拼接生成新对象，因此在这一类问题上没有显示「回溯」的过程，但是如果使用 StringBuilder 拼接字符串就另当别论。
在这里把它们单独作为一个题型，是希望朋友们能够注意到这个非常细节的地方。

• 17. 电话号码的字母组合（中等），题解；
• 784. 字母大小写全排列（中等）；
• 22. 括号生成（中等） ：这道题广度优先遍历也很好写，可以通过这个问题理解一下为什么回溯算法都是深度优先遍历，并且都用递归来写。

题型四：游戏问题

回溯算法是早期简单的人工智能，有些教程把回溯叫做暴力搜索，但回溯没有那么暴力，回溯是有方向地搜索。「力扣」上有一些简单的游戏类问题，解决它们有一定的难度，大家可以尝试一下。

• 51. N 皇后（困难）：其实就是全排列问题，注意设计清楚状态变量，在遍历的时候需要记住一些信息，空间换时间；
• 37. 解数独（困难）：思路同「N 皇后问题」；
• 488. 祖玛游戏（困难）
• 529. 扫雷游戏（困难）

（欢迎大家补充。）

参考资料

• liuyubobobo 老师在慕课网上开设的课程《玩转算法面试》代码仓库。
• https://leetcode-cn.com/problems/permutations/solution/hui-su-suan-fa-python-dai-ma-java-dai-ma-by-liweiw/