2020牛客国庆集训派对day5

2020牛客国庆集训派对day5

题目	A	B	C	D	E	F	G	H	I	J	K
solved	-	-	✔		-	-	-	✔	-	-	✔

^{✔：比赛时通过；：赛后通过；⚪：比赛时尝试了未通过；-：比赛时未尝试}

---

C Great Deceiver【构造】

solved by Sstee1XD. 3:31(+7)
题意：问你在$1-n$中有多少个数字在$k$进制与$-k$进制表示下结果相同。
题解：转换一下就是要求正负进制下只有奇数位有数字的数字有多少个。转换过程中记录下最后一位出现数字的偶数位在哪里，之后所有的奇数位都可以变成$k-1$，然后分别计算当前位限制的最大数字情况下和其他情况下数字的数量，注意最后一位直接加上数字$+1$。做这道题目和队友有分歧，导致卡了很久。

#include
using namespace std;
typedef long long ll;
const int inf = 0x3f3f3f3f;

#define endl "\n"
#define dbg(x...)             \
    do {                      \
        cout << #x << " -> "; \
        err(x);               \
    } while (0)

void err() {	cout << endl;}
template <class T, class... Ts>
void err(const T& arg, const Ts&... args) {
    cout << arg << ' ';
    err(args...);
}
ll n, k;
ll a[200];

ll qpow(ll a, ll b) {
	ll res = 1;
	for (; b; b >>= 1) {
		if (b & 1) res *= a;
		a *= a;
	}
	return res;
}

void solve(){
	int f = 1, even = 0;
	while (n >= k) {
		a[f] = n % k;
		n /= k;
		if (f&1) {
			f++;
			continue;
		}
		if (a[f]) {
			even = f;
		}
		f++;
	}
	a[f] = n;
    if (f % 2 == 0) {
		if (a[f]) even = f;
		f--;
	}
	if (even) a[1] = k - 1;
	ll ans = a[1] + 1;
	while (f > 1) {
		if (f < even) a[f] = k - 1;
		ans += a[f] * qpow(k, f / 2);
		f -= 2;
	}
	cout << ans << endl;
}

int main(){
	ios::sync_with_stdio(false);
	cin.tie(0);cout.tie(0);
	cin >> n >> k;
	solve();
	return 0;
}

D Exact Measurement【贪心】

solved by lllllan.(-)

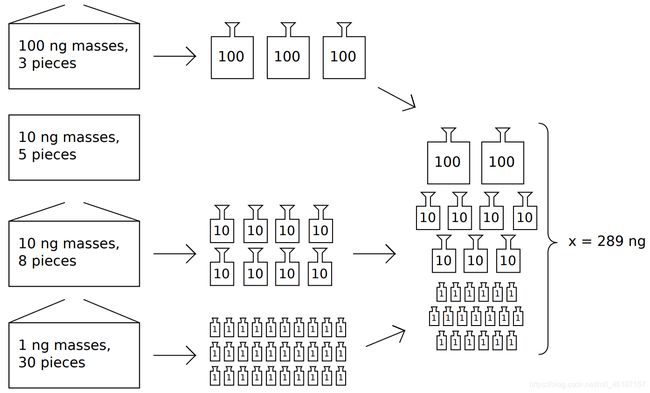
题意： 有一个X（1 ≤ x ≤ 10¹⁸）单位重量的物品，你有n个箱子，每个箱子里有q个10^k单位重量的砝码。如果能用箱子里的砝码准确称出物品的重量，请用最少的箱子并输出其编号（1到n）。否则输出-1.

题解： 通过图我们就要很明确一点，小砝码数量足够多时可以替代大砝码，而大砝码无法替代小砝码。所以我们需要从X的个位，逐位寻找合适砝码。可将10^k单位重量的砝码放入K队列中，为满足使用最少的箱子的原则，给所有的箱子都做上是否打开的标记，已打开的优先使用，其次是砝码数量较多的优先使用。而K位上用剩下的砝码，则可以插入K+1队列中使用。

#include
#include
#include
using namespace std;
typedef long long ll;
const int inf = 0x3f3f3f3f;

#define endl "\n"
#define dbg(x...)             \
    do {                      \
        cout << #x << " -> "; \
        err(x);               \
    } while (0)

void err() {	cout << endl;}
template <class T, class... Ts>
void err(const T& arg, const Ts&... args) {
    cout << arg << ' ';
    err(args...);
}

const int N = 1e5 + 10;
ll x, n, res[24];
int cnt, sum, ans[N];
struct box {
	int id, isans;
	ll q;
	bool operator<(const box &a)const{
		if(a.isans == isans)	return a.q > q;	//从大到小 
		return a.isans > isans;
	}
} ;
priority_queue<box> Q[24];

void run() {
	for (int i = 0; i < n; i++){
		ll k, q;
		scanf("%lld%lld", &k, &q);
		Q[k].push({i + 1, 0, q * pow(10, k)});
	}
	ll tmp = 1;
	while(x) {
		res[cnt++] = x % 10 * tmp;
		x /= 10;
		tmp *= 10;
	}
	for(int i = 0; i < cnt; i++){
		while(!Q[i].empty()){
			box u = Q[i].top(); Q[i].pop();
			if (res[i]) {
				if(u.q  >= res[i]){
					u.q -= res[i] ;
					res[i] = 0;
					if(!u.isans)	ans[sum++] = u.id;
					Q[i + 1].push({u.id, 1, u.q});
				} else {
					res[i] -= u.q;
					if(!u.isans)	ans[sum++] = u.id;
				}
			} else {
				Q[i + 1].push({u.id, u.isans, u.q});
			}
		}
		if(res[i]){
			printf("-1\n");
			return;
		}
	}
	printf("%d\n", sum);
	for(int i = 0; i < sum; i++)
		printf("%d ", ans[i]);
}

int main() {
	scanf("%lld%lld", &x, &n);
	run();
	return 0;
}

H Fraud Busters【签到】

solved by Tryna.00:10:21(+)

#include
using namespace std;
typedef long long ll;
const int inf = 0x3f3f3f3f;

#define endl "\n"
#define dbg(x...)             \
    do {                      \
        cout << #x << " -> "; \
        err(x);               \
    } while (0)

void err() {	cout << endl;}
template <class T, class... Ts>
void err(const T& arg, const Ts&... args) {
    cout << arg << ' ';
    err(args...);
}
int n, f[1010];
char ch[1010][15], st[15];
int main(){
	cin >> st;
	cin >> n;
	for(int i = 1; i <= n; i++){
		cin >> ch[i];
	}
	int cnt = n;
	for(int i = 1; i <= n; i++){
		for(int j = 0;j <= 8; j++){
			if(st[j] == '*') continue;
			if(st[j] != ch[i][j]){
				f[i] = 1;
				cnt--;
				break;
			}
		}	
	}
	cout << cnt << endl;
	for(int i = 1; i<= n; i++){
		if(f[i] == 0) cout << ch[i] << endl;
	}
	return 0;
}

K Knockout Racing【签到】

solve by Sstee1XD. 00:29(+1)

#include
using namespace std;
typedef long long ll;
const int inf = 0x3f3f3f3f;

#define endl "\n"
#define dbg(x...)             \
    do {                      \
        cout << #x << " -> "; \
        err(x);               \
    } while (0)

void err() {	cout << endl;}
template <class T, class... Ts>
void err(const T& arg, const Ts&... args) {
    cout << arg << ' ';
    err(args...);
}
int n, m, ql, qr, t;

int l[1050], r[1050];

void solve() {
	for (int i = 1; i <= n; ++i) {
		cin >> l[i] >> r[i];
	}
	while (m--) {
		int ans = 0;
		cin >> ql >> qr >> t;
		for (int i = 1; i <= n; ++i) {
			int tmp, f;
			if (l[i] == r[i]) tmp = l[i];
			else {
				tmp = t % (r[i] - l[i]);
				f = t / (r[i] - l[i]);
				if (f & 1) tmp = r[i] - tmp;
				else tmp += l[i];
			}
			if (tmp >= ql && tmp <= qr) ans++;
		}
		cout << ans << endl;
	}
}

int main(){
	ios::sync_with_stdio(false);
	cin.tie(0);cout.tie(0);
	cin >> n >> m;
	solve();
	return 0;
}