了解下余弦相似度在文本处理中的应用
大家好啊,我是董董灿!
昨天写了一篇介绍词向量的文章:5分钟搞懂什么是词嵌入,里面说到:通过把文本转换为词向量,就可以十分方便的计算两者之间的关系,看看哪两个单词更为相近。
比如有四个单词:“猫”、“狗”、“鱼”、“跑”,通过向量转换可以得到如下的向量:
- 猫:[0.2, 0.7]
- 狗:[0.3, 0.9]
- 鱼:[-0.5, 0.2]
- 跑:[0.8, -0.1]
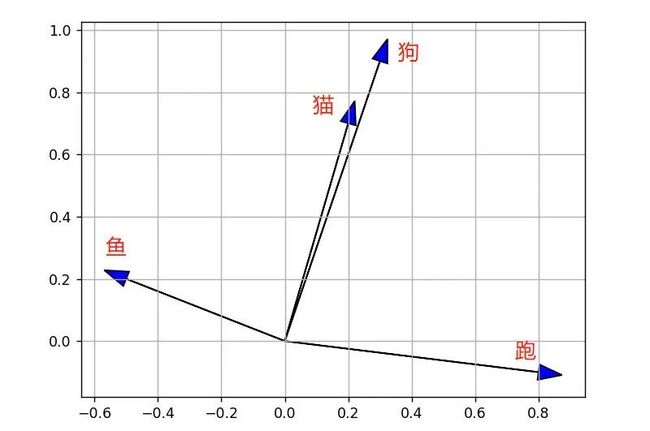
将四个向量画在坐标图上如下图。
我们通过观察可以很轻松的看出来,“猫”和“狗”的两个向量很相近,“鱼”和“跑”代表的两个向量则相差很远。
这是因为猫和狗都是动物,而鱼和跑则没有什么关联性。
但是计算机不像人一样是可以观察的,它只能通过计算来评估两个单词代表的向量是否相近。所以得有一个计算指标,让计算机知道哪两个向量之间关系更紧密。
这就用到了余弦相似度。
1、还记得什么是余弦相似度吗
余弦相似度的计算公式如下:
cos_similarity = (A · B) / (||A|| * ||B||)
其中,A和B分别表示两个向量。A · B表示向量A和向量B的点积,||A||和||B||表示向量A和向量B的范数(或长度)。
- 两个向量之间的夹角越小,余弦相似度值越接近于1,说明两个向量靠的越近,代表的两个单词就越相关。
- 两个向量之间的夹角越大,余弦相似度值越远离于1,说明两个向量靠的越远,代表的两个单词就越不相关。
通过这个计算公式,就可以得到两个向量之间的余弦相似度。
下面是一个python计算余弦相似度的代码实现,用它来计算一下
import numpy as npdef cos_sim(a, b):a_norm = np.linalg.norm(a)b_norm = np.linalg.norm(b)cos = np.dot(a,b)/(a_norm * b_norm)return coscat = [0.2, 0.7]dog = [0.3, 0.9]fish = [-0.5, 0.2]run = [0.8, -0.1]print("cos_sim of cat and dog is " + str(cos_sim(cat, dog)))print("cos_sim of cat and fish is " + str(cos_sim(cat, fish)))print("cos_sim of fish and run is " + str(cos_sim(fish, run)))
结果如下:
通过计算也可以得到相同的结论:“猫”和“狗”余弦相似度接近1,说明两个向量更为接近,而“鱼”和“跑”则接近-1,说明两个向量代表的单词相差很远。
2、余弦相似度用在什么场景
余弦相似度的应用还是很常见的,不过大部分集中在自然语言处理相关的任务中,比如:
在文本分类任务中,我们需要将一段文本划分到不同的类别中。
为了实现这个目标,通常会使用词向量来表示文本,然后通过计算文本之间的余弦相似度,判断文本在语义上是否相似,从而更好地进行分类。
在推荐系统任务中,需要根据用户的行为和喜好推荐适合他们的产品。余弦相似度可以用来衡量用户与商品之间的相似性,从而根据用户的历史行为来推荐相关的商品。
在图像相似性比较任务中,可以将图像表示为向量形式,然后通过计算余弦相似度来衡量图像之间的相似性。
余弦相似度虽然可以方便快速的判断两个向量之间的关系,但是它也是有缺点的,那就是它并没有考虑向量的绝对大小,只关注方向,这一点在公式中也可以看出来。
也正是因为这些局限的存在,在一些场景下人们可能会倾向于其他方法来衡量两个向量的相似性。
但是这个可以与"勾股定理”媲美的简单的计算公式,却可以在很多模型中表现的很好,也着实让我有些吃惊,有时候,简单就是最有效的,不是吗?